Fondamenti di Probabilità
(Press ? for help, n and p for next and previous slide; usage hints)
andrea venuti (License Information)
A separate Howto for Text-To-Speech (TTS) with emacs-reveal exists as well...
Fondamenti di probabilita’
General
La prima parte consiste nel trovare metodi razionali per la caratterizazione di fenomeni casuali La seconda parte invece consiste nel descrivere gli eventi ( segnali ) aletori dipendenti dal tempo.
Definizioni generali
- Evento : risultato osservato;
- Descrizione di un singolo evento : associazione di un singolo evento del fenomeno casuale ad un valore reale mediante l’uso della probabilita’ ( prob calssica / prob. statistica);
- Insieme Campionario Insieme formato da tutti i possibili risultati di un esperimento. Può essere continuo o discreto;
- Classe Insieme C formato da sottoinsiemi di S;
- Campo Si denota con \(\mathcal{F}\) ed è una particolare classe in cui ogni elemento costituisce un evento L’utilizzo dei campi permette di definire in modo analitico gli eventi di modo che questi siano sempre associati a risultati dell’ esperimento. Ad esempio in caso nel caso del lancio di una moneta abbiamo \(\mathcal{F}=\{\oslash, testa, croce, S\}\) con \(S=\{testa,croce\}\) e con \(P(s_i)=\frac{1}{2}\).
- Variabile Aleatoria Associa ad ogni risultato di un esperimento, oppure ad un sottoinsieme di risultati, un valore reale permettendo implicitamente una numerazione dello spazio campionario. Puo’ essere discreta oppure continua a seconda se l’insieme campionario e’ discreto o continuo. In questo seondo caso si considerano solo intervalli.
- Descrizione di esperimento Raggruppamento dei possibili eventi di un fenomeno casuale con associazione di un evento casuale ad un valore reale ( variabili aleatorie ) e rappresentazione mendiante la Funzione di distribuzione e la funzione della densita’ di probabilita’ il cui gli argomenti sono le variabili aleatorie.
- Indici di un esperimento Insieme di valori che permettono di caratterizzare un esperimento conoscendo le v.a. senza ricorrre allo studio delle funzioni che lo descrivono.
La Probabilita’
in riferimento alla fig 1 la definizione classica di probabilita’ e’ :
\(P(A \cup B)=P(A)+P(B) - P(A \cap B) \leq P(A) + P(B)\)
che si giustifica la definizione, infatti se la probalilita’ e’ la misura della superficie allora la probabilita’ totale e’ la somma delle superficie dei sottoinsiemi A e B meno la supericie comune;
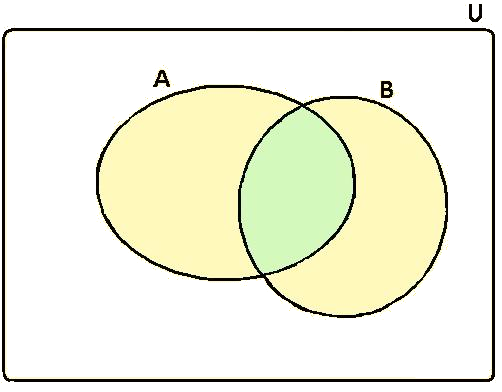
Figure 1: \(P(A \cup B)=P(A)+P(B) - P(A \cap B)\)
Postulati della Probabilità
- \(P(A) \geq 0 \ \forall A\);
- \(P(S)=1\) \(P(\oslash)=0\);
- \(\forall \ A \cap B=\oslash \ \rightarrow P(A \cup B)=P(A)+P(B)\) eventi mutuamente esclusivi;
- \(\forall \ A \cap B \neq \oslash \ \rightarrow P(A \cup B)=P(A)+P(B) - P(A \cap B)\)
Teorema dell’esperimento
Usando le proprieta’ della FDD una funzione \(G(x)\) reale rappresenta una funzione di distribuzione se :
- \(G:R \rightarrow R_x\)
- \(G(\infty)=1\)
- \(G(-\infty) =0\)
- \(G(x_1) \leq G(x_2) \ \forall \ x_1 \leq x_2\)
COROLLARIO : Se esiste una funzione \(G(x)\) con le proprietà di cui sopra allora esiste un esperimento \(E\) t.c. la funzione di distribuzione dell’esperimento è coincide con \(G(x)\).
Descrizione dell’evento mediante funzioni
Funzione di distribuzione di probabilita’ - FDP
La funzione di distribuzione di probabilità (FDP), detta anche funzione di ripartizione cumulativa di una variabile aleatoria X è una funzione che descrive la probabilità che X assuma un valore inferiore o uguale a un certo valore \(x_i\). In altre parole, la FDP fornisce la probabilità che l’evento \(X \leq x_i\) si verifichi e ne rappresenta il grafico. La definizione formale e’
Proprieta’ della FDP
- La FDP e’ una funzione non decrescente;
- La FDP e’ sempre compresa tra 0 e 1;
- \(F_X(- \infty)=0\) evento impossibile;
- \(F_X(\infty)=1\) evento certo;
- Se X e’ una variabile aleatoria continua la FDP è una funzione continua infatti :
- Se X e’ una v.a. discreta il grafico della FDP presenta discontinuità ( limiti dx e sx tendono ad un valore diverso ) a sx della v.a. l’ampiezza del salto indica la probabilità associata all’i-esima v.a. \(F_X ( x_i ) = P_X ( X \leq x_i ) \neq 0\). Ad esempio nel lancio di un dado vale 1/6. Da notare che le probabilità a sx e a dx volgono, rispettivamente, \(P_X ( X \leq x_0 )\) e \(1 - P_X(X \leq x_0)\) e per ogni intervallo \([x_i,x_i + 1(\) la \(F_X(x_i)\) rimane costante .
Metodo Pratico di calcolo della FDP
Sia N il numero di esperimenti o realizzazione della v.a. la funzione fdp, e sia \(\#\) il numero di prove con l esito sperato.
Funzione di densita’ di probabilita’ - fdp
La fdp una funzione che descrive la probabilità che una variabile aleatoria continua assuma un certo valore. È una funzione non negativa, il cui integrale su tutto l’insieme di definizione di S è uguale a 1. La fdp può essere utilizzata per calcolare probabilità, medie, varianze e per modellare fenomeni reali. Definita come :
La fdp rappresenta una probabilita’ solo quando si considera un intervallo e non quando e’ puntuale cioe :
Proprieta’ della fdp
- \(f(x) \geq 0\);
- \(\int_{-\infty}^{\infty} f(x)dx =F_X(\infty) - F_X(-\infty)=1\);
- \(P(\{x_1 < x(s) \leq x_2\})=\int_{x_1}^{x_2}f(x)dx\);
La probabilità che X assuma un valore in un certo intervallo \([x_1, x_2]\) è uguale all’integrale della PDF su quell’intervallo:
Metodo pratico di calcolo fdp
Sia N il numero di esperimenti o realizzazione della v.a. la funzione fdp, e sia \(\#\) il numero di prove con l esito sperato.
Posizione di due v.a.
v.a. indipendenti
Due v.a. sono indipendenti quando
\(p(X_0 , X_1 ) = p(X_0 ) · p(X_1 )\)
Probabilita’ condizionata - teorema di Bayes
probabilita’ che si verifichi l’evento \(x_1\) quando si verifica \(x_0\)
\(p(X_1 |X_0 ) = \frac{p(X_1 , X_0 )}{p(X_0 )}\)
- P(X1∣ X0) rappresenta la probabilità dell’evento X1 dato che l’evento X0 si è verificato, detta anche probabilità condizionata di X1 rispetto a X0.
- P(X0) e P(X1) sono le probabilità marginali di X0 e X1 rispettivamente, cioè le probabilità di X0 e X1 senza alcuna condizione.
In termini più intuitivi, il teorema di Bayes afferma che la probabilità che un evento X0 si verifichi, data l’occorrenza di un evento X1, è proporzionale alla probabilità dell’evento X1, dato che l’evento X0 si è verificato, moltiplicata per la probabilità dell’evento X0, e divisa per la probabilità dell’evento X1.
Probabilità Congiunta
Modella il concetto di un esperimento descritto con n v.a. ( teoria per n = 2 ) :
Siano X, Y due v.a. definite come :
Funzione di distribuzione di probabilita’ - FDP
In modo analogo a come si e’ definita l’analoga funzione per una variabile si ha che la FDP in piu’ variabili e’ definita come
in cui
Vettore di v.a.
Sia \(\vec{x}=[x_1, \ldots, x_n]\) un vettore di v.a. allora la definizione di funzione di probabilita’ diviene come quella indicata nella \eqref{eq:0102}
Momenti di una v.a
Sono indici che descrivono il comportamento di una v.a. e l’ordine indica il numero di v.a. considerate
Definizione di momento
Permettono la caratterizzazione di un p.a. anche senza conoscere la FDP associata ad una v.a.
In generale, il k-esimo momento di una variabile casuale discreta X è definito come:
mentre per il caso continuo
in cui
- \(\mu^k\) è il k-esimo momento centrale;
- \(x_i\) è la variabile casuale;
Definizione di momento centrale
I momenti centrali di una variabile aleatoria sono una serie di statistiche che forniscono informazioni riguardo alla distribuzione della variabile stessa. Essi sono calcolati rispetto alla media della distribuzione e aiutano a descrivere la forma e la dispersione dei dati e per il caso discreto sono definiti come :
- \(\mu^k\) è il k-esimo momento centrale;
- \(x_i\) è la variabile casuale;
- \(m\) è la media della variabile casuale.
Media o Valore atteso
Analoga alla media matematica. quando la media e’ nulla allora una probabilita’ equa significa che si ha la stessa probabilita’ che un evento si verifichi o meno. Dal punto di vista analiticho per v.a. continue la f(x) e’ simmetrica.
- Media del primo ordine
- v.a. discrete : \(m_x = \sum_{x_i} p_i x_i\)
- v.a. continua : \(m_x = \int_{-\infty}^{\infty} xf(x) d_x\)
- Media del secondo ordine
- v.a. discrete : \(m_{xy} = \sum_{i,j}x_i y_j f(x,y)\)
- v.a. continue : \(m_{xy} = \int_{X} \int_{Y} xy f_{XY}(x, y) d_x d_y\)
- Medie marginali (o valori attesi marginali): Le medie marginali di X e Y sono definite rispettivamente come:
- \(m_x = \int x f_X(x) dx\)
\(m_y = \int y f_Y(y) dy\)
dove \(f_X(x)\) e \(f_Y(y)\) sono le densità marginali di X e Y rispettivamente.
- Medie marginali (o valori attesi marginali): Le medie marginali di X e Y sono definite rispettivamente come:
Potenza Nel caso di v.a. con media nulla la varianza si ha :
\begin{equation} \label{pot} P = E\{x^2(\omega)\}=\int x^2f_x(x)d_x \end{equation}
Varianza, Covarianza e Correlazione
E’ una misura della variabilita’ della v.a. . La sola media non e’ sufficente a caratterizzare una v.a. allora si definisce una variabile intesa come la sommatoria della differenze tra la media e le singole v.a. . Essendo una sommatoria puo’ accadere che la somma sia nulla e allora si usa il quadrato delle singole differenze. Da notare che \(x_i - m_i\) rappresenta una distanza.
- Varianza ( primo ordine )
- v.a. discreta : \(\sigma^2 = \sum_{i}(x_i - m_i)^2\);
- v.a. continua : \(\sigma^2 = \int_{-\infty}^{\infty} (x - m)^2 f(x) d_x\)
- Da notare che la varianza puo’ essere definita come \(\sigma^2=P - m\)
- Scarto quadratico medio o deviazione standard Definito come \(\sigma=\sqrt{\sigma ^2}\) ed e’ utilizzato per poter confrontare media e varianza.
- Correlazione Questa equazione deriva da quella della covarianza ma con v.a. a media nulla e le conclusioni sono le stesse della covarianza.
- Covarianza ( secondo ordine ) Indica come le variazioni di una variabile sono associate alle variazioni dell’altra variabile.
Autocovarianza - Autocorrelazione
- autocovarianza
- Tempo discreto : \(C_{xx}[n,n+m]= \iint_{-\infty}^{\infty} (x_n - m_{x[n]})(x_{(n+m)} - m_{x[n+m]}) f_{x[n],x[n+m]}(X,Y)d_X d_Y\)
- Tempo continuo : \(C_{xx}(t,t+\tau)=\iint_{-\infty}^{\infty}(x(t) - m_t)(x(t + \tau) - m_{t+\tau})f_{xx}(x(t),x(t + \tau))\)
- autocorrelazione Funzione del valor medio dipendente solamente da due istanti diversi:
- Tempo discreto : \(R_{xx}[x_n,x_{n+m}]=\iint_{-\infty}^{\infty} x_n x_{(n+m)} f_{xx}(x[n],x[n+m])d_X d_Y\);
- Tempo continuo: \(R_{xx}(\tau)=\int_{-\infty}^{\infty} x(t)x(t-\tau)d_t\)
Statistiche del secondo ordine - Crossvarianza
Misura la similarita’ tra due serie temporali diverse, ma ad intervalli temporali diversi. È utilizzata per valutare se due serie temporali sono correlate tra loro e come questa correlazione varia nel tempo. Può essere usata per esaminare le relazioni causa-effetto tra due serie temporali o per identificare se ci sono legami temporali tra di esse. Da come risultato una matrice ed e’ definita come segue :
Sia \(x=x(t_1)\) e \(y=y(t_2)\) allora \(CR_{xy}(x,y)=E\{(x - \mu_x)(y -\mu_y)^*\}\)
che per
- Sistemi a tempo discreto vale
- Sistemi a tempo continuo vale
Statistiche del secondo ordine - Crossrelazione
La cross-correlazione è una misura di quanto due segnali o serie temporali siano simili tra loro in momenti diversi. Confronta due serie temporali per vedere se esiste una relazione tra di esse. È utilizzata per determinare se ci sono ritardi o avanzamenti tra i due segnali e per identificare eventuali relazioni di causa-effetto. Ad esempio, la cross-correlazione potrebbe essere utilizzata per determinare se c’è una relazione tra la temperatura e la domanda di energia elettrica: una forte correlazione positiva potrebbe indicare che un aumento della temperatura porta a un aumento della domanda di energia elettrica.
Sia \(x=x(t_1)\) e \(y=y(t_2)\) allora \(CC_{xy}(x,y)=E\{(x)(y)^*\}\)
- Tempo discreto : sia \(\tau \in Z\) allora la crossrelazione e’ definita come \(CC_{xy}[\tau]=E=\{XY^T\}E\{x[n]y[n+\tau]^T\}=\sum_{t=-\infty}^{\infty}x[n]y[n+\tau]^T\)
Nel caso reale si ha che
Tempo continuo
\(CC_{xy}(\tau)=E\{x(t)y^*(t - \tau)\}= \int_{-\infty}^{\infty}x(t)y^*(t-\tau) d_t\)
V.A. Gaussiane
Definizione di v.a. gauassiana
E’ un tipo di variabile aleatoria continua completamente caratterizzata da due parametri: la sua media (o valore atteso) e la sua deviazione standard.
La distribuzione gaussiana è simmetrica rispetto alla sua media e ha la forma di una curva a campana, comunemente nota come curva a forma di “campana di Gauss”. Questa distribuzione è ampiamente utilizzata in statistica e in molti campi scientifici e ingegneristici per modellare fenomeni naturali, e molte leggi del mondo reale tendono a seguire questa distribuzione.
La funzione di densità di probabilità di una variabile casuale gaussiana è data dalla formula:
Densità di probabilità di N v.a. congiuntamente Gaussiane
Rappresenta la generalizzazione della distribuzione Gaussiana al caso multivariato. Sia x un vettore composto da N v.a. congiuntamente Gaussiane è caratterizzato da una funzione di densita’ di probabilita’ pdf avente la seguente espressione:
in cui \(C_x\) e’ la matrice di covarianza del vettore x
Nel caso di 2 v.a. si ha che
Proprieta’ della gaussiana
- se \(\rho\) è zero (v.a. incorrelate), la densita’ di probabilita’ diventa separabile nelle variabili \(x\) e \(y\) (v.a. statisticamente indipendenti );
- le pdf marginali sono ancora Gaussiane;
- le pdf condizionali sono ancora Gaussiane. In particolare, vale
dove
- \(m_{x|y}=m_1 +\rho \frac{\sigma_1}{\sigma_2}(y - m_y)\)
- \(\sigma^2=(1 -\rho^2)\sigma_x\)
V.A. Complessa
Definizione
Dalla definizione ricavata dal * a pag 190 una v.a. complessa è una funzione del tipo \(Z(\omega):\Omega \rightarrow \mathbb{C}\) avente struttura di un numero complesso \(z(\omega)=x(\omega)+jv(\omega)\) e pertanto la relazione tra DDP e ddp è ridefinita come segue :