Analisi 1 - Richiami di teoria
Table of Contents
1. Definizioni
1.1. Maggiorante
Un numero \(M \in \mathbb{R}\) è maggiorante di un insieme \(A \subseteq \mathbb{R}\) se:
\[ \forall a \in A, \quad a \leq M \]
Cioè, tutti gli elementi dell'insieme sono minori o uguali a \(M\).
1.2. Minorante
Un numero \(m \in \mathbb{R}\) è minorante di un insieme \(A \subseteq \mathbb{R}\) se:
\[ \forall a \in A, \quad a \geq m \]
Cioè, tutti gli elementi dell'insieme sono maggiori o uguali a \(m\).
1.3. Massimo
Un elemento \(M \in A\) è il massimo dell’insieme \(A\) se:
- \(M\) è maggiorante di \(A\),
- e \(M \in A\).
In simboli:
\[ \forall a \in A, \quad a \leq M \quad \text{e} \quad M \in A \]
1.4. Minimo
Un elemento \(m \in A\) è il minimo dell’insieme \(A\) se:
- \(m\) è minorante di \(A\),
- e \(m \in A\).
In simboli:
\[ \forall a \in A, \quad a \geq m \quad \text{e} \quad m \in A \]
1.5. Punto Stazionario
Sia \(f: \mathbb{R} \to \mathbb{R}\) una funzione derivabile in un punto \(x_0\). Si dice che \(x_0\) è un punto stazionario di \(f\) se:
\[ f'(x_0) = 0 \]
Cioè, la derivata della funzione si annulla in quel punto.
Significato intuitivo :
Nel punto \(x_0\), la pendenza della tangente è zero ⇒ la tangente è orizzontale. Questo succede tipicamente in:
- massimi locali
- minimi locali
- punti di flesso orizzontali
- Esempi
- \(f(x) = x^2\) → \(f'(x) = 2x\) → \(f'(0) = 0\) ⇒ punto stazionario in \(x = 0\) (è un minimo)
- \(f(x) = -x^2\) → punto stazionario in \(x = 0\) (è un massimo)
- \(f(x) = x^3\) → \(f'(x) = 3x^2\), quindi \(f'(0) = 0\) ⇒ punto stazionario in \(x = 0\), ma non è massimo né minimo → è un punto di flesso orizzontale
1.5.1. *Nota importante
Un punto stazionario non è necessariamente* un punto di massimo o minimo. Serve un'analisi ulteriore (es. seconda derivata) per capire la natura del punto.
1.6. Punto di accumulazione
Un punto \(x \in \mathbb{R}\) è un punto di accumulazione di un insieme \(A \subseteq \mathbb{R}\) se:
\[ \forall \varepsilon > 0, \; \exists a \in A \setminus \{x\} \; \text{tale che} \; |a - x| < \varepsilon \]
Cioè, in ogni intorno di \(x\) ci sono infiniti punti di \(A\) diversi da \(x\).
1.7. Punto di bordo (o punto di frontiera)
Un punto \(x \in \mathbb{R}\) è un punto di bordo di un insieme \(A\) se:
\[ \forall \varepsilon > 0, \; B_\varepsilon(x) \cap A \neq \emptyset \; \text{e} \; B_\varepsilon(x) \cap (\mathbb{R} \setminus A) \neq \emptyset \]
Cioè, ogni intorno di \(x\) contiene almeno un punto di \(A\) e almeno un punto non in \(A\).
1.8. Rappresentazione grafica
Ecco una rappresentazione grafica dell'insieme \(A = (1, 4) \cup \{5, 6\}\):
- Il tratto blu rappresenta l'intervallo aperto \((1, 4)\), che non include i bordi 1 e 4.
- I punti blu scuro (cerchi pieni) a \(x = 5\) e \(x = 6\) sono punti isolati di \(A\).
- Il punto rosso a \(x = 6\) è il massimo di \(A\).
- Il punto verde a \(x = 4\) è un punto di accumulazione.
- I punti ciano a \(x = 1\) e \(x = 5\) sono punti di bordo.
- 1 è punto di bordo Ogni intorno di 1 contiene punti di \(A\) (perché \(A\) contiene tutti i numeri maggiori di 1) ma 1 non appartiene ad \(A\) (l'intervallo è aperto) Quindi: 1 è punto di bordo.
- 4 è punto di bordo Ogni intorno di 4 contiene punti di \(A\) (da sinistra). 4 non appartiene ad \(A\). Quindi: 4 è punto di bordo.
- 5 è punto di bordo 5 appartiene ad \(A\), ma ogni intorno contiene anche numeri vicini (come 5.01, 4.99) non in \(A\). Quindi: 5 è punto di bordo.
- 6 è punto di bordo Anche 6 è isolato: ogni suo intorno contiene punti non in \(A\), e 6 stesso è in \(A\). Quindi: 6 è punto di bordo.
Conclusione: il bordo di \(A\) è \[\boxed{\{1, 4, 5, 6\}}\]
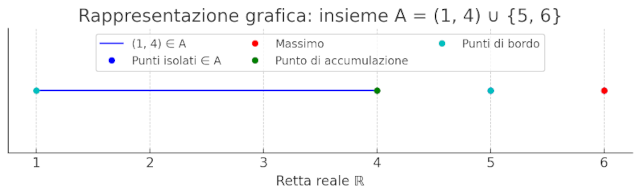
Figure 1: rappresetazione delle definizioni
1.9. Interno di \(A\)
L’**interno** di un insieme è l’insieme di tutti i punti interni, cioè quei punti per cui esiste un intorno completamente contenuto in \(A\). Ogni punto di \((1, 4)\) ha un intorno interamente contenuto in \(A\) ⇒ fanno parte dell’interno. I punti 5 e 6 non hanno intorni che stanno interamente in \(A\) (sono isolati).
Quindi:
\[ \text{interno}(A) = (1, 4) \]
1.10. Esterno di \(A\)
L’**esterno** è l’insieme dei punti che hanno un intorno disgiunto da \(A\), cioè completamente fuori da \(A\). Qualunque punto molto lontano da \(A\), ad esempio \(0\), \(10\), o anche \(4.5\), ha un piccolo intorno che non tocca \(A\). Tuttavia, punti vicini a 1, 4, 5, 6 sono troppo vicini a \(A\) per avere intorni disgiunti.
Quindi:
\[ \text{esterno}(A) = (-\infty, 1) \cup (4, 5) \cup (6, +\infty) \]
—
1.11. Chiusura di \(A\)
La chiusura di un insieme è data da:
\[ \text{chiusura}(A) = A \cup \text{bordo}(A) \]
Abbiamo:
- \(A = (1, 4) \cup \{5, 6\}\)
- Bordo di \(A\) = \(\{1, 4, 5, 6\}\)
Quindi:
Chiusura:
\[ \text{chiusura}(A) = [1, 4] \cup \{5, 6\} \]
Nota che l'intervallo \((1,4)\) diventa chiuso in \([1,4]\) nella chiusura.
1.12. Riepilogo
| Concetto | Insieme risultante |
|---|---|
| Interno | \((1, 4)\) |
| Esterno | \((-\infty, 1) \cup (4, 5) \cup (6, +\infty)\) |
| Bordo | \(\{1, 4, 5, 6\}\) |
| Chiusura | \([1, 4] \cup \{5, 6\}\) |
Ecco la rappresentazione grafica dei concetti topologici per l’insieme \(A = (1, 4) \cup \{5, 6\}\):
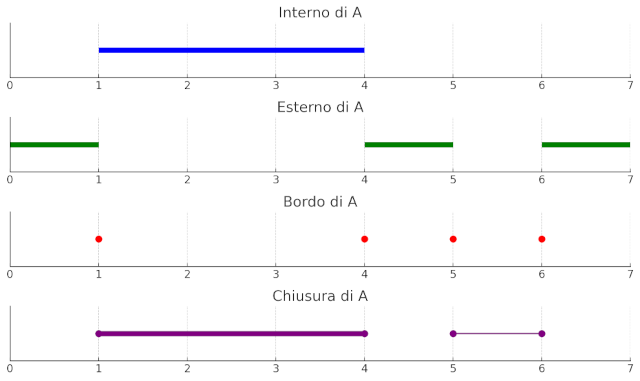
Figure 2: rappresetazione delle definizioni
- Interno: solo i punti dell’intervallo aperto \((1, 4)\).
- Esterno: tutte le zone completamente fuori da \(A\), cioè prima di 1, tra 4 e 5, e dopo 6.
- Bordo: i punti \(\{1, 4, 5, 6\}\), evidenziati come cerchi rossi.
- Chiusura: unisce tutto \(A\) più i suoi punti di bordo, cioè \([1, 4] \cup \{5, 6\}\).
Se vuoi, posso anche farti un riepilogo simbolico su un’unica linea con notazione grafica tipo diagramma o timeline!