Analisi 1 - Teoremi Vari in \(R\)
Table of Contents
- 1. Definizione di Limite
- 2. Derivata
- 3. Differenziabilita'
- 4. Teorema degli zeri (di Bolzano)
- 5. Teorema di Bolzano-Weirstrass
- 6. Teorema di WEIRSTRASS
- 7. Teorema di Fermat
- 8. Teorema di Rolle
- 9. Teorema di Lagrange
- 10. Teorema di Cauchy
1. Definizione di Limite
Sia \( f: A \subseteq \mathbb{R} \to \mathbb{R} \) una funzione e \( x_0 \) un punto di accumulazione per \( A \). Si dice che: \[ \lim_{x \to x_0} f(x) = L \in \mathbb{R} \] se per ogni \( \epsilon > 0 \) esiste un \( \delta > 0 \) tale che: \[ \forall x \in A, \quad 0 < |x - x_0| < \delta \implies |f(x) - L| < \epsilon. \]
1.1. Interpretazione:
- Per ogni "tolleranza" \( \epsilon \) sull'output \( f(x) \), esiste un intorno \( (x_0 - \delta, x_0 + \delta) \) in cui \( f(x) \) rimane entro \( L \pm \epsilon \).
1.2. Dimostrazione
Esempio: Dimostrare che \( \lim_{x \to 2} (3x - 1) = 5 \).
1.2.1. Passo 1: Fissare \( \epsilon > 0 \)
Dobbiamo trovare \( \delta > 0 \) tale che: \[ 0 < |x - 2| < \delta \implies |(3x - 1) - 5| < \epsilon. \]
1.2.2. Passo 2: Manipolare la disuguaglianza
Semplifichiamo \( |(3x - 1) - 5| \): \[|3x - 6| = 3|x - 2| < \epsilon.\] Quindi: \[|x - 2| < \frac{\epsilon}{3}.\]
1.2.3. Passo 3: Scelta di \( \delta \)
Basta prendere \( \delta = \frac{\epsilon}{3} \).
- Verifica: Se \( 0 < |x - 2| < \delta \), allora: \[ 3|x - 2| < 3 \cdot \frac{\epsilon}{3} = \epsilon. \]
1.3. Conclusione:
Per ogni \( \epsilon > 0 \), scegliendo \( \delta = \frac{\epsilon}{3} \), la definizione è soddisfatta.
1.4. Casi Speciali
- Limite infinito: \[ \lim_{x \to x_0} f(x) = +\infty \iff \forall M > 0, \exists \delta > 0 \text{ tale che } 0 < |x - x_0| < \delta \implies f(x) > M. \]
- Limite per \( x \to \infty \) \[ \lim_{x \to +\infty} f(x) = L \iff \forall \epsilon > 0, \exists N > 0 \text{ tale che } x > N \implies |f(x) - L| < \epsilon. \]
1.5. Perché è Importante?
- Fondamento dell'analisi: Tutti i concetti di continuità, derivata e integrale si basano sui limiti.
- Verifica rigorosa: Evita intuizioni errate (es. \( \lim_{x \to 0} \frac{\sin x}{x} = 1 \) non è ovvio senza una dimostrazione ε-δ).
2. Derivata
La derivata di una funzione \( f \) in un punto \( x_0 \) è il limite del rapporto incrementale quando l'incremento \( h \) tende a zero:
\[f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}\]
2.1. Interpretazione:
- Geometrica: La derivata \( f'(x_0) \) rappresenta la pendenza della retta tangente al grafico di \( f \) nel punto \( (x_0, f(x_0)) \).
- Fisica: Corrisponde alla velocità istantanea di variazione di \( f \) in \( x_0 \).
2.2. Dimostrazione della Derivata (Esempio Concreto)
Esempio: Calcolare la derivata di \( f(x) = x^2 \) in \( x_0 = 3 \).
2.2.1. Passo 1: Scrivere il rapporto incrementale
\[\frac{f(3 + h) - f(3)}{h} = \frac{(3 + h)^2 - 9}{h} = \frac{9 + 6h + h^2 - 9}{h} = \frac{6h + h^2}{h}\]
2.2.2. Passo 2: Semplificare
\[\frac{6h + h^2}{h} = 6 + h \quad \text{(per } h \neq 0\text{)}\]
2.2.3. Passo 3: Calcolare il limite per \( h \to 0 \)
\[f'(3) = \lim_{h \to 0} (6 + h) = 6\]
2.2.4. Conclusione: La derivata di \( f(x) = x^2 \) in \( x_0 = 3 \) è \( 6 \).
2.3. Derivata come Operatore Lineare
La derivata soddisfa le seguenti proprietà:
- Linearità: \[ (af + bg)' = af' + bg'\]
- Regola del Prodotto: \[ (f \cdot g)' = f'g + fg' \]
- Regola della Catena: \[ (f(g(x)))' = f'(g(x)) \cdot g'(x) \]
2.4. Esempio di Non-Derivabilità
Funzione: \( f(x) = |x| \) in \( x_0 = 0 \).
- Il rapporto incrementale destro e sinistro sono diversi: \[ \lim_{h \to 0^+} \frac{|h|}{h} = 1, \quad \lim_{h \to 0^-} \frac{|h|}{h} = -1 \]
- Conclusione: \( f \) non è derivabile in \( 0 \) (punto angoloso).
2.5. Importanza della Derivata
- Ottimizzazione: Trova massimi/minimi (es. in economia o fisica).
- Equazioni Differenziali: Modellano fenomeni dinamici (es. crescita di popolazioni).
3. Differenziabilita'
La differenziabilità è una proprietà più forte della semplice derivabilità. Una funzione \( f \colon \mathbb{R} \to \mathbb{R} \) si dice differenziabile in \( x_0 \) se può essere approssimata localmente da una funzione lineare (una retta) con un errore che tende a zero più rapidamente di \( |x - x_0| \).
3.1. Definizione Formale
\( f \) è differenziabile in \( x_0 \) se esiste un numero \( m \in \mathbb{R} \) (la derivata \( f'(x_0) \)) tale che:
\[f(x_0 + h) = f(x_0) + m h + o(h) \quad \text{per } h \to 0,\]
dove \( o(h) \) è un termine di errore che soddisfa:
\[\lim_{h \to 0} \frac{o(h)}{h} = 0.\]
3.2. Equivalente:
Esiste una retta \( y = f(x_0) + f'(x_0)(x - x_0) \) (tangente) che approssima \( f \) intorno a \( x_0 \) con errore trascurabile rispetto a \( |h| \).
3.3. Dimostrazione della Differenziabilità (Esempio)
Funzione: \( f(x) = x^2 \) in \( x_0 = 1 \).
3.3.1. Passo 1: Calcolare la derivata
\[f'(1) = \lim_{h \to 0} \frac{(1 + h)^2 - 1}{h} = \lim_{h \to 0} (2 + h) = 2.\]
3.3.2. Passo 2: Scrivere lo sviluppo di Taylor al primo ordine
\[f(1 + h) = f(1) + f'(1)h + o(h) \implies (1 + h)^2 = 1 + 2h + o(h).\]
3.3.3. Passo 3: Verificare la condizione \( o(h) \)
Sottraendo i termini noti:
\[o(h) = (1 + h)^2 - 1 - 2h = h^2.\]
Osserviamo che:
\[\lim_{h \to 0} \frac{h^2}{h} = \lim_{h \to 0} h = 0.\]
Quindi \( h^2 = o(h) \), e la funzione è differenziabile.
3.4. Interpretazione Geometrica
- Approssimazione lineare: La retta tangente \( y = 1 + 2(x - 1) \) approssima \( f(x) = x^2 \) vicino a \( x = 1 \).
- Errore: L'errore \( h^2 \) è "più piccolo" di \( h \) per \( h \to 0 \) (es. se \( h = 0.1 \), \( h^2 = 0.01 \)).
3.5. Teorema: Differenziabilità implica Continuità
Se \( f \) è differenziabile in \( x_0 \), allora è continua in \( x_0 \).
3.5.1. Dimostrazione:
Dalla definizione di differenziabilità:
\[\lim_{h \to 0} f(x_0 + h) = f(x_0) + \lim_{h \to 0} (m h + o(h)) = f(x_0).\]
3.5.2. Controesempi
- Funzione non derivabile: \( f(x) = |x| \) in \( x_0 = 0 \).
- Non esiste una retta tangente unica ⇒ non è differenziabile.
- Funzione derivabile ma non \( C^1 \):
\[ f(x) = \begin{cases} x^2 \sin(1/x) & \text{se } x \neq 0, \\ 0 & \text{se } x = 0. \end{cases} \]
- È differenziabile in \( 0 \) (\( f'(0) = 0 \)), ma \( f' \) non è continua in \( 0 \).
4. Teorema degli zeri (di Bolzano)
Sia \(f: [a, b] \to \mathbb{R}\) una funzione continua sull’intervallo chiuso \([a, b]\). Se:
\[ f(a) \cdot f(b) < 0 \]
cioè se \(f(a)\) e \(f(b)\) hanno segni opposti, allora esiste almeno un punto \(c \in (a, b)\) tale che:
\[ f(c) = 0 \]
—
4.1. Significato intuitivo:
Se una funzione continua "parte da un valore negativo e arriva a uno positivo" (o viceversa), deve necessariamente attraversare lo zero almeno una volta.
—
4.2. Esempio:
Sia \(f(x) = x^2 - 2\), e consideriamo l’intervallo \([1, 2]\):
- \(f(1) = 1^2 - 2 = -1\)
- \(f(2) = 4 - 2 = 2\)
- \(f\) è continua in \([1, 2]\)
- \(f(1) \cdot f(2) = -1 \cdot 2 < 0\)
⇒ Per il teorema degli zeri, esiste \(c \in (1, 2)\) con \(f(c) = 0\), cioè:
\[ c = \sqrt{2} \]
4.3. Dimostrazione
(La dimostrazione è simile se \(f(a) > 0\) e \(f(b) < 0\))
Dimostrazione (con metodo di bisezione + completezza dei reali)
4.3.1. Definiamo l’insieme:
\[ S = \{ x \in [a, b] \mid f(x) < 0 \} \]
Osserviamo che:
- \(a \in S\) perché \(f(a) < 0\)
- \(S\) è non vuoto e limitato superiormente (da \(b\))
4.3.2. Esiste il supremo \(c = \sup S\) (perché \(\mathbb{R}\) è completo)
4.3.3. Mostriamo che \(f(c) = 0\)
a. Supponiamo per assurdo che \(f(c) > 0\)
- La funzione \(f\) è continua in \(c\)
- Quindi, esiste \(\delta > 0\) tale che:
\[ \forall x \in (c - \delta, c), \quad f(x) > 0 \]
- Ma \(c = \sup S\), quindi esistono punti di \(S\) arbitrariamente vicini a sinistra di \(c\), cioè con \(f(x) < 0\)
- Contraddizione: in \((c - \delta, c)\), \(f(x) > 0\), quindi nessun punto lì può avere \(f(x) < 0\) Quindi \(f(c) \not> 0\)
b. Supponiamo ora che \(f(c) < 0\)
- Con continuità, esiste \(\delta > 0\) tale che:
\[ \forall x \in (c, c + \delta), \quad f(x) < 0 \]
- Ma allora esistono punti \(x > c\) tali che \(f(x) < 0\), quindi \(x \in S\), cioè \(c\) non sarebbe il supremo di \(S\) Quindi \(f(c) \not< 0\)
4.3.4. Concludiamo:
\[ f(c) = 0 \]
Quindi: esiste almeno un punto \(c \in (a, b)\) tale che \(f(c) = 0\). ■
NB : il teorema non vale senza continuità!
4.4. Rappresentazione visuale
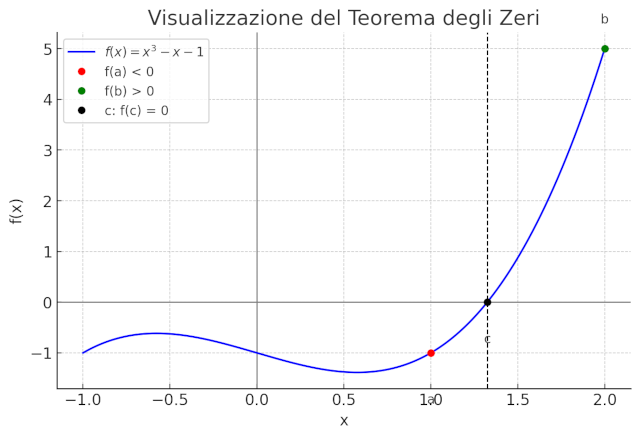
Figure 1: rappresetazione visuale del teorema
- La curva blu rappresenta la funzione continua \(f(x) = x^3 - x - 1\).
- Il punto rosso è \(f(a) < 0\), e il punto verde è \(f(b) > 0\), con \(a = 1\), \(b = 2\).
- Il punto nero è \(c\), lo zero garantito dal teorema: \(f(c) = 0\).
La linea tratteggiata nera mostra visivamente che la funzione attraversa l’asse \(x\), cioè si annulla in un punto \(c \in (a, b)\).
Questa è proprio la situazione descritta dal teorema: se una funzione continua cambia segno in un intervallo, deve annullarsi almeno una volta all’interno. Vuoi che ti mostri anche il procedimento numerico per trovare \(c\) (es. con metodo di bisezione)?
5. Teorema di Bolzano-Weirstrass
Ogni successione limitata \( \{x_n\} \) in \( \mathbb{R} \) (o più generalmente in \( \mathbb{R}^n \)) ammette una sottosuccessione convergente.
In altre parole, se \( \{x_n\} \) è tale che \( |x_n| \leq M \) per qualche \( M > 0 \), allora esiste una sottosuccessione \( \{x_{n_k}\} \) e un punto \( L \in \mathbb{R} \) tali che: \[ \lim_{k \to +\infty} x_{n_k} = L. \]
5.1. Dimostrazione Analitica
5.1.1. Passo 1: Costruzione della sottosuccessione monotona
Poiché \( \{x_n\} \) è limitata, esiste un intervallo \( [a, b] \) che la contiene. Usiamo il metodo di bisezione per trovare un punto di accumulazione.
- Dividiamo \( [a, b] \) in due sottointervalli:
- \( [a, \frac{a+b}{2}] \) e \( [\frac{a+b}{2}, b] \).
- Almeno uno dei due contiene infiniti termini della successione. Scegliamo quello con infiniti termini e chiamiamolo \( I_1 \).
- Iteriamo il procedimento:
- Ripetiamo la bisezione su \( I_1 \), ottenendo \( I_2 \), e così via.
- Otteniamo una successione di intervalli \( I_1 \supseteq I_2 \supseteq \dots \) con \( \text{diam}(I_k) \to 0 \).
- Costruiamo la sottosuccessione:
- Scegliamo \( x_{n_1} \in I_1 \), poi \( x_{n_2} \in I_2 \) con \( n_2 > n_1 \), e così via.
- Per costruzione, \( \{x_{n_k}\} \) è una successione di Cauchy e quindi converge a un punto \( L \in \bigcap_{k} I_k \).
5.1.2. Conclusione
Abbiamo estratto una sottosuccessione convergente.
5.1.3. Dimostrazione Grafica (Visualizzazione)
Immaginiamo di rappresentare i termini \( \{x_n\} \) su una retta reale:
Successione limitata: Tutti i punti \( x_n \) sono contenuti in un intervallo \( [a, b] \).
a -----------------[x₃ x₁ x₄ x₂ ...]------------------ b
Bisezione:
- Dividiamo \( [a, b] \) in due metà.
- Almeno una metà (es. la sinistra) contiene infiniti punti.
a -------[x₃ x₁ ...]-------|-------[x₄ x₂ ...]------- b
Selezione della sottosuccessione:
- Continuiamo a selezionare la metà con infiniti punti.
- I termini estratti \( x_{n_k} \) si "addensano" verso un punto \( L \).
L ← x_{n_1}, x_{n_2}, x_{n_3}, ...
5.1.4. Esempio concreto
Consideriamo la successione oscillante: \[ x_n = (-1)^n \frac{n}{n+1} = \{-1/2, 2/3, -3/4, 4/5, \dots\} \]
- Limitata: \( |x_n| \leq 1 \).
- Sottosuccessioni convergenti:
- Se \( n_k = 2k \) (pari), \( x_{n_k} \to 1 \).
- Se \( n_k = 2k-1 \) (dispari), \( x_{n_k} \to -1 \).
Osservazioni
- Essenzialità della limitatezza: Se \( \{x_n\} \) non è limitata (es. \( x_n = n \)), il teorema non vale.
- Generalizzazioni: Vale in \( \mathbb{R}^n \) (per successioni in spazi euclidei) e in ogni spazio metrico compatto.
Questo teorema è fondamentale per dimostrare altri risultati, come il Teorema di Weierstrass (sull'esistenza di massimi e minimi) e il Teorema di Heine-Borel (sulla compattezza in \( \mathbb{R}^n \)).
6. Teorema di WEIRSTRASS
Se \(f: [a, b] \to \mathbb{R}\) è continua su un intervallo chiuso e limitato \([a, b]\), allora:
- \(f\) raggiunge un massimo assoluto in \([a, b]\)
- \(f\) raggiunge un minimo assoluto in \([a, b]\)
Cioè, esistono \(x_{\min}, x_{\max} \in [a, b]\) tali che:
\[ f(x_{\min}) \leq f(x) \leq f(x_{\max}) \quad \text{per ogni } x \in [a, b] \]
6.1. Dimostrazione
La dimostrazione si basa su due proprietà chiave degli intervalli chiusi e limitati:
- Compattezza (per successioni) di \([a, b]\).
- Continuità di \( f \), che preserva la convergenza.
Supponiamo per assurdo che \( f \) non sia limitata superiormente. Allora, per ogni \( n \in \mathbb{N} \), esiste \( x_n \in [a, b] \) tale che: \[ f(x_n) > n. \] La successione \( \{x_n\} \) è contenuta in \([a, b]\), che è compatto (per il Teorema di Bolzano-Weierstrass). Quindi, esiste una sottosuccessione \( \{x_{n_k}\} \) convergente a un punto \( x_0 \in [a, b] \).
Per la continuità di \( f \): \[ \lim_{k \to +\infty} f(x_{n_k}) = f(x_0) \quad (\text{che è un valore finito}). \] Ma per costruzione \( f(x_{n_k}) > n_k \), e poiché \( n_k \to +\infty \), si avrebbe \( f(x_0) = +\infty \), il che è assurdo perché \( f(x_0) \in \mathbb{R} \).
Conclusione: \( f \) è limitata superiormente.
Sia \( M = \sup_{x \in [a, b]} f(x) \). Per definizione di estremo superiore, esiste una successione \( \{y_n\} \subseteq [a, b] \) tale che: \[ \lim_{n \to +\infty} f(y_n) = M. \] Di nuovo, per compattezza, esiste una sottosuccessione \( \{y_{n_k}\} \) convergente a un punto \( y_0 \in [a, b] \). Per continuità: \[ f(y_0) = \lim_{k \to +\infty} f(y_{n_k}) = M. \] Quindi \( y_0 \) è un punto di massimo assoluto.
Ripetendo il ragionamento con \( -f \) (che è anch’essa continua), si dimostra l’esistenza del minimo assoluto.
Conclusione Abbiamo mostrato che \( f \) ammette sia massimo che minimo assoluti in \([a, b]\).
Osservazioni
- L’ipotesi di intervallo chiuso e limitato è essenziale. Ad esempio, \( f(x) = x \) su \( (0, 1) \) non ha massimo.
- La continuità è cruciale: una funzione discontinua come \( f(x) = 1/x \) su \( (0, 1] \) non è limitata.
6.2. Grafico:
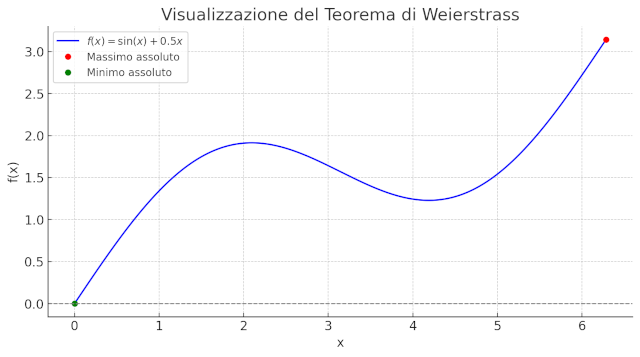
Figure 2: rappresetazione visuale del teorema
- La funzione \(f(x) = \sin(x) + 0.5x\) è continua su \([0, 2\pi]\)
- Il punto verde è il minimo assoluto (valore più basso)
- Il punto rosso è il massimo assoluto (valore più alto)
Come garantito dal teorema, entrambi esistono e si trovano nell’intervallo chiuso.
NB : se l’intervallo non è chiuso o limitato il teorema non vale più!
7. Teorema di Fermat
Se \( f \) ha un massimo/minimo locale in \( c \) ed è derivabile in \( c \), allora \( f'(c) = 0 \).
Quindi, nel punto \( c \) dove \( f \) raggiunge il massimo/minimo interno:
- La tangente al grafico è orizzontale (\( f'(c) = 0 \).
- Questo garantisce l’esistenza del punto critico richiesto da Rolle.
NB: è un teorema locale (fornisce una proprietà dei punti di max/min).
7.1. Esempio per capire il legame
Considera \( f(x) = \sin(x) \) su \([0, \pi]\):
- \( f(0) = f(\pi) = 0 \).
- Per Weierstrass, \( f \) ha massimo in \( c = \pi/2 \).
- Per Fermat, in \( c = \pi/2 \) la derivata \( f'(\pi/2) = \cos(\pi/2) = 0 \).
Senza Fermat, non potremmo concludere che \( f'(c) = 0 \) nei punti di max/min!
8. Teorema di Rolle
Sia \( f: [a, b] \to \mathbb{R} \) una funzione tale che:
- Continua su \([a, b]\),
- Derivabile su \((a, b)\),
- \( f(a) = f(b) \).
Allora esiste almeno un punto \( c \in (a, b) \) tale che \( f'(c) = 0 \).
8.1. Dimostrazione Analitica
8.1.1. Passo 1: Applicazione del Teorema di Weierstrass
Poiché \( f \) è continua su \([a, b]\), per il Teorema di Weierstrass ammette massimo \( M \) e minimo \( m \) assoluti.
8.1.2. Passo 2: Analisi dei casi
- Caso 1 (Funzione costante): Se \( f(x) = k \) per ogni \( x \in [a, b] \), allora \( f'(x) = 0 \) per ogni \( x \in (a, b) \). Il teorema è banalmente vero.
- Caso 2 (Funzione non costante): Poiché \( f(a) = f(b) \), almeno uno tra \( M \) e \( m \) deve essere raggiunto in un punto interno \( c \in (a, b) \).
8.1.3. Passo 3: Applicazione del Teorema di Fermat
- Se \( c \) è un punto di massimo/minimo interno e \( f \) è derivabile in \( c \), allora \( f'(c) = 0 \) (per il Teorema di Fermat sui punti critici).
8.1.4. Conclusione: Esiste almeno un \( c \in (a, b) \) dove \( f'(c) = 0 \).
8.2. Dimostrazione Grafica
Rappresentazione della funzione:
- Disegniamo \( f(x) \) continua su \([a, b]\) con \( f(a) = f(b) \).
- Se \( f \) non è costante, deve "salire e/o scendere" per poi ritornare al valore iniziale.
f(x) | f(a)=f(b) |-----•-------• | / \ | / \ |___/___________\___ x a bInterpretazione geometrica:
- La derivata \( f'(c) \) rappresenta la pendenza della retta tangente.
- Nel punto \( c \) dove \( f \) raggiunge un massimo o minimo, la tangente è orizzontale (\( f'(c) = 0 \)).
f(x) | | /•\ | / \ |____/_____\___ x c
8.3. Esempio Numerico
Sia \( f(x) = x^3 - 3x^2 \) su \([0, 3]\).
- Verifica ipotesi:
- \( f(0) = 0 \) e \( f(3) = 0 \) ⇒ \( f(0) = f(3) \).
- \( f \) è continua e derivabile su tutto \( \mathbb{R} \).
- Calcolo del punto critico:
- \( f'(x) = 3x^2 - 6x \).
- \( f'(c) = 0 \Rightarrow 3c^2 - 6c = 0 \Rightarrow c = 0 \) o \( c = 2 \).
- Solo \( c = 2 \) è interno a \( (0, 3) \).
Conclusione: Il punto \( c = 2 \) soddisfa \( f'(2) = 0 \).
8.4. Osservazioni
- Ipotesi necessarie:
- Se \( f \) non è continua o derivabile, il teorema può fallire (es. \( f(x) = |x| \) su \([-1, 1]\)).
- Se \( f(a) \neq f(b) \), non è garantito che \( f'(c) = 0 \) (es. \( f(x) = x \) su \([0, 1]\)).
- Generalizzazione: È un caso speciale del Teorema di Lagrange (o del valor medio).
9. Teorema di Lagrange
Sia \( f: [a, b] \to \mathbb{R} \) una funzione tale che:
- Continua su \([a, b]\),
- Derivabile su \((a, b)\).
Allora esiste almeno un punto \( c \in (a, b) \) tale che: \[ f'(c) = \frac{f(b) - f(a)}{b - a}. \]
Interpretazione : Esiste un punto \( c \) in cui la pendenza della tangente (\( f'(c) \)) coincide con la pendenza della retta secante che collega \((a, f(a))\) e \((b, f(b))\).
9.1. Dimostrazione Grafica e Visuale
- Disegna il grafico di \( f(x) \) sull'intervallo \([a, b]\).
- Traccia la retta secante passante per \((a, f(a))\) e \((b, f(b))\):
- La sua equazione è: \[ y = \frac{f(b) - f(a)}{b - a}(x - a) + f(a). \]
Per applicare Rolle, definiamo una funzione \( g(x) \) che misura la distanza verticale tra \( f(x) \) e la secante: \[ g(x) = f(x) - \left[ \frac{f(b) - f(a)}{b - a}(x - a) + f(a) \right]. \]
- Proprietà di \( g(x) \):
- \( g(a) = g(b) = 0 \) (per costruzione).
- \( g \) è continua su \([a, b]\) e derivabile su \((a, b)\) (perché \( f \) lo è).
Per Rolle, esiste \( c \in (a, b) \) tale che \( g'(c) = 0 \). Calcoliamo \( g'(x) \): \[ g'(x) = f'(x) - \frac{f(b) - f(a)}{b - a}. \] Imponendo \( g'(c) = 0 \): \[ f'(c) = \frac{f(b) - f(a)}{b - a}. \]
Interpretazione grafica:
- Nel punto \( c \), la tangente a \( f(x) \) è parallela alla secante.
9.2. Esempio Numerico
Sia \( f(x) = x^2 \) su \([1, 3]\).
- Pendenza della secante: \[ \frac{f(3) - f(1)}{3 - 1} = \frac{9 - 1}{2} = 4. \]
- Derivata: \( f'(x) = 2x \).
- Punto \( c \): \[ f'(c) = 4 \Rightarrow 2c = 4 \Rightarrow c = 2 \in (1, 3). \]
Verifica grafica:
- La tangente in \( x = 2 \) ha equazione \( y = 4x - 4 \).
- La secante ha equazione \( y = 4x - 3 \).
- Sono parallele (stessa pendenza).
9.3. Osservazioni
- Significato geometrico:
- Il teorema garantisce che, in condizioni "regolari", esiste almeno un punto in cui la tangente è parallela alla corda tra gli estremi.
- Controesempi:
- Se \( f \) non è derivabile (es. \( f(x) = |x| \) su \([-1, 1]\)), il teorema fallisce.
- Se \( f \) non è continua agli estremi, non è applicabile.
- Generalizzazioni:
- È alla base di molti risultati fondamentali, come la Regola di L'Hôpital e lo studio della monotonia delle funzioni.
10. Teorema di Cauchy
Siano \( f, g \colon [a, b] \to \mathbb{R} \) due funzioni tali che:
- Continue su \([a, b]\),
- Derivabili su \((a, b)\),
- \( g'(x) \neq 0 \) per ogni \( x \in (a, b) \).
Allora esiste almeno un punto \( c \in (a, b) \) tale che: \[ \frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(c)}{g'(c)}. \]
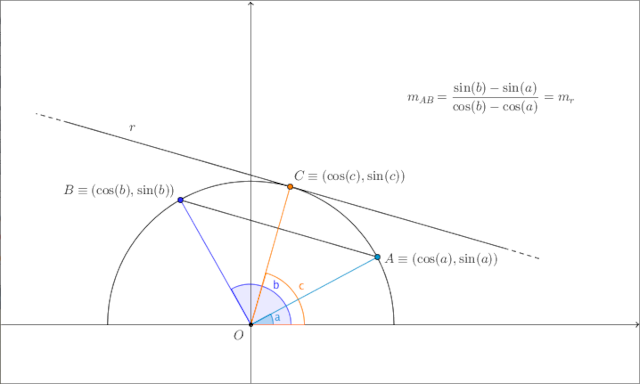
Figure 3: rappresetazione visuale del teorema
10.1. Dimostrazione
10.1.1. Passo 1: Verificare che \( g(b) \neq g(a) \)
- Per il Teorema di Rolle, se \( g(b) = g(a) \), esisterebbe un \( c \in (a, b) \) con \( g'(c) = 0 \).
- Ma per ipotesi \( g'(x) \neq 0 \) in \((a, b)\), quindi necessariamente \( g(b) \neq g(a) \).
10.1.2. Passo 2: Costruzione della funzione ausiliaria
Definiamo una funzione \( h(x) \) combinando \( f \) e \( g \) per soddisfare le ipotesi di Rolle: \[ h(x) = f(x) - \left( \frac{f(b) - f(a)}{g(b) - g(a)} \right) g(x). \]
- Proprietà di \( h \):
- \( h \) è continua su \([a, b]\) e derivabile su \((a, b)\) (perché \( f \) e \( g \) lo sono).
- \( h(a) = h(b) \): \[ h(a) = f(a) - \left( \frac{f(b) - f(a)}{g(b) - g(a)} \right) g(a), \] \[ h(b) = f(b) - \left( \frac{f(b) - f(a)}{g(b) - g(a)} \right) g(b). \] Sottraendo, si verifica che \( h(a) = h(b) \).
10.1.3. Passo 3: Applicazione del Teorema di Rolle a \( h(x) \)
Esiste \( c \in (a, b) \) tale che \( h'(c) = 0 \). Calcoliamo \( h'(x) \): \[ h'(x) = f'(x) - \left( \frac{f(b) - f(a)}{g(b) - g(a)} \right) g'(x). \] Imponendo \( h'(c) = 0 \): \[ f'(c) = \left( \frac{f(b) - f(a)}{g(b) - g(a)} \right) g'(c), \] da cui otteniamo la tesi: \[ \frac{f'(c)}{g'(c)} = \frac{f(b) - f(a)}{g(b) - g(a)}. \]
—
10.2. Relazione con il Teorema di Lagrange
- Se \( g(x) = x \), il Teorema di Cauchy si riduce al Teorema di Lagrange: \[ \frac{f(b) - f(a)}{b - a} = f'(c). \]
10.3. Interpretazione Grafica
- Curve parametriche:
- Considera le funzioni \( f \) e \( g \) come coordinate parametriche di una curva \( \gamma(t) = (g(t), f(t)) \).
- Il rapporto \( \frac{f(b) - f(a)}{g(b) - g(a)} \) è la pendenza della corda che collega \( \gamma(a) \) e \( \gamma(b) \).
- Il teorema afferma che esiste un punto \( \gamma(c) \) in cui la tangente alla curva è parallela alla corda.
10.4. Esempio Numerico
Siano \( f(x) = x^2 \) e \( g(x) = x^3 \) su \([1, 2]\).
- Calcolo dei rapporti: \[ \frac{f(2) - f(1)}{g(2) - g(1)} = \frac{4 - 1}{8 - 1} = \frac{3}{7}, \] \[ \frac{f'(x)}{g'(x)} = \frac{2x}{3x^2} = \frac{2}{3x}. \]
- Punto \( c \): \[ \frac{2}{3c} = \frac{3}{7} \Rightarrow c = \frac{14}{9} \in (1, 2). \]
10.5. Osservazioni
- Importanza:
- È fondamentale per dimostrare la Regola di de l'Hôpital.
- Generalizza il Teorema di Lagrange a funzioni vettoriali.
- Controesempi:
- Se \( g'(x) = 0 \) in qualche punto, il teorema non vale (es. \( g(x) = \text{costante} \)).