Analisi 2 - Studio delle funzioni in $R^2$

1. Studio di Funzioni in $\mathbb{R}^2$
2. Approfondimenti nel punto di sella

1. Studio di Funzioni in $\mathbb{R}^2$

✅ Funzione scelta:

\[ f(x, y) = x^3 - 3xy^2 \]

Questa funzione è chiamata "monkey saddle", e presenta punti di sella. Possiamo anche aggiungere un vincolo per trovare estremi vincolati.

1.1. Studio non vincolato (libero)

1.1.1. Derivate parziali (gradiente)

\[ f_x = \frac{\partial f}{\partial x} = 3x^2 - 3y^2 \quad ; \quad f_y = \frac{\partial f}{\partial y} = -6xy \]

1.1.2. Punti critici (gradiente nullo)

Poniamo il gradiente uguale a 0:

\begin{cases} 3x^2 - 3y^2 = 0 \\ -6xy = 0 \end{cases}

⇒

\begin{cases} x^2 = y^2 \Rightarrow x = \pm y \\ xy = 0 \end{cases}

Esaminiamo i due casi da $xy = 0$:

Se $x = 0 \Rightarrow y = 0$
Se $y = 0 \Rightarrow x = 0$

Unico punto critico:

\[ (x, y) = (0, 0) \]

1.1.3. Hessiana e classificazione del punto

Derivate seconde:

\[ f_{xx} = 6x,\quad f_{yy} = -6x,\quad f_{xy} = f_{yx} = -6y \]

Punto critico: $(0, 0)$

Hessiana in $(0,0)$:

\[ H = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \Rightarrow \det(H) = 0 \]

⚠️ Il test dell’Hessiana non fornisce informazioni → dobbiamo analizzare direttamente la forma della funzione.

Osserviamo $f(x, y) = x(x^2 - 3y^2)$. Lungo:

$y = 0 \Rightarrow f(x,0) = x^3$
$x = 0 \Rightarrow f(0,y) = 0$
$y = x \Rightarrow f(x,x) = x(x^2 - 3x^2) = -2x^3$

➡️ Il segno della funzione cambia nei dintorni di $(0,0)$, quindi è un punto di sella.

1.2. Studio con vincolo

Usiamo il vincolo:

\[g(x,y) = x^2 + y^2 = 1 \quad \text{(il cerchio unitario)}\]

1.2.1. Lagrangiana

\[ \mathcal{L}(x, y, \lambda) = f(x, y) - \lambda (x^2 + y^2 - 1) = x^3 - 3xy^2 - \lambda(x^2 + y^2 - 1) \]

1.2.2. Derivate parziali

\[\frac{\partial \mathcal{L}}{\partial x} = 3x^2 - 3y^2 - 2\lambda x = 0 \tag{1}\]

\[\frac{\partial \mathcal{L}}{\partial y} = -6xy - 2\lambda y = 0 \tag{2}\]

\[\frac{\partial \mathcal{L}}{\partial \lambda} = -(x^2 + y^2 - 1) = 0 \tag{3}\]

1.2.3. Risoluzione del sistema

Da (2):

\[ (-6x - 2\lambda)y = 0 \Rightarrow y = 0 \quad \text{o} \quad \lambda = -3x \]

Caso 1: $y = 0$
Da (3): $x^2 = 1 \Rightarrow x = \pm 1$

Da (1):

\[3x^2 - 2\lambda x = 0 \Rightarrow 3 - 2\lambda x = 0 \Rightarrow \lambda = \frac{3}{2x}\]

Verificato.

✅ Due punti vincolati:

\[ (1, 0), \quad (-1, 0) \]

Valori della funzione:
- $f(1, 0) = 1^3 - 3(1)(0)^2 = 1$
- $f(-1, 0) = (-1)^3 = -1$
Massimo vincolato in $(1,0)$, minimo in $(-1,0)$
Caso 2: $\lambda = -3x$

Sostituisco in (1):

\[ 3x^2 - 3y^2 - 2(-3x)x = 3x^2 - 3y^2 + 6x^2 = 9x^2 - 3y^2 = 0 \Rightarrow 3x^2 = y^2 \]

Da (3):

\[ x^2 + y^2 = 1 \Rightarrow x^2 + 3x^2 = 4x^2 = 1 \Rightarrow x^2 = \frac{1}{4} \Rightarrow x = \pm \frac{1}{2},\quad y = \pm \frac{\sqrt{3}}{2} \]

✅ Altri 4 punti critici:

\[ \left(\pm \frac{1}{2}, \pm \frac{\sqrt{3}}{2} \right) \]

Calcoliamo i valori di $f$:

\[f\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right) = \left(\frac{1}{2}\right)^3 - 3 \cdot \frac{1}{2} \cdot \left(\frac{3}{4}\right) = \frac{1}{8} - \frac{9}{8} = -1\]

\[f\left(\frac{1}{2}, -\frac{\sqrt{3}}{2}\right) = \frac{1}{8} - (-\frac{9}{8}) = \frac{10}{8} = 1.25\]

E così via.

1.3. Piano tangente

Per calcolare il piano tangente alla superficie $z = f(x, y) = x^3 - 3xy^2$ in un punto $(x_0, y_0)$, usiamo:

\[z = f(x_0, y_0) + f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0)\]

Prendiamo ad esempio il punto $(1, 0)$:

$f(1, 0) = 1$
$f_x(1, 0) = 3(1)^2 - 3(0)^2 = 3$
$f_y(1, 0) = -6(1)(0) = 0$

Piano tangente:

\[z = 1 + 3(x - 1) = 3x - 2\]

1.4. Conclusione

Tipo	Punto	Valore $f(x,y)$	Note
Punto critico libero	(0,0)	0	Punto di sella
Estremo vincolato minimo	$(-1, 0)$, $\left(\tfrac{1}{2}, \tfrac{\sqrt{3}}{2}\right)$	−1	minimo su vincolo
Estremo vincolato massimo	$(1, 0)$, $\left(\tfrac{1}{2}, -\tfrac{\sqrt{3}}{2}\right)$	1, 1.25	massimo su vincolo
Piano tangente	Punto $(1,0)$	Piano: $z = 3x - 2$

1.5. Grafico

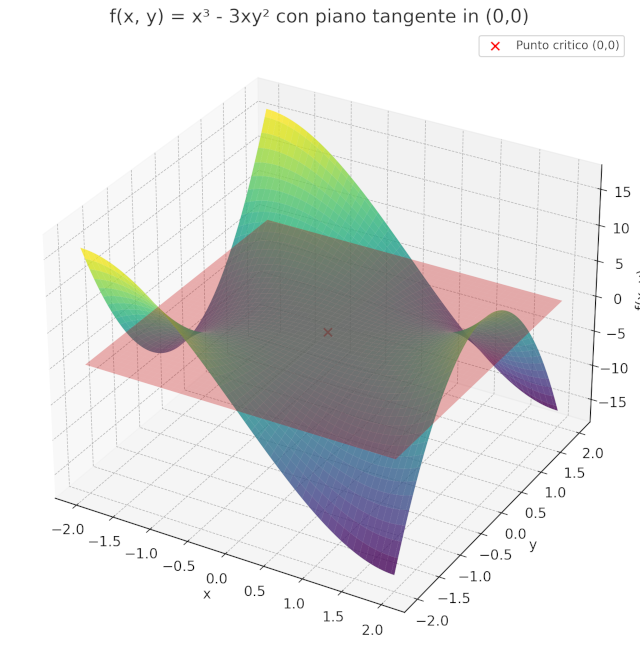
Figure 1: grafico della funzione

2. Approfondimenti nel punto di sella

Hai notato che nello studio del punto critico $(0,0)$ per la funzione:

\[ f(x, y) = x^3 - 3xy^2 \]

sono stati presi alcuni cammini particolari: $y = 0$, $x = 0$, e $y = x$. Ora ti spiego perché vengono utilizzati questi percorsi nello studio.

Obiettivo: Classificare il punto critico (0, 0)

Abbiamo trovato che $(0,0)$ è un punto stazionario (cioè $\nabla f = 0$), ma la matrice Hessiana in quel punto è nulla:

$$ H(0, 0) =

\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}

⇒ det(H) = 0 $$

Quindi non possiamo usare il test della Hessiana per sapere se si tratta di:

Minimo locale
Massimo locale
Punto di sella

2.0.1. Strategia: Esaminare la funzione lungo traiettorie

Quando il test della Hessiana fallisce (cioè $\det H = 0$), un metodo classico è analizzare il comportamento della funzione lungo direzioni diverse che passano per $(0,0)$. Questo si chiama studio per restrizione a curve.

Ecco perché abbiamo guardato:

▶ Lungo $y = 0$

$$ f(x, 0) = x³ - 3x ⋅ 0² = x³ ⇒

\begin{cases} x > 0 \Rightarrow f(x, 0) > 0 \\ x < 0 \Rightarrow f(x, 0) < 0 \end{cases}

▶ Lungo $x = 0$

\[ f(0, y) = 0 - 3 \cdot 0 \cdot y^2 = 0 \]

→ la funzione è nulla lungo quest’asse.

▶ Lungo $y = x$

$$ f(x, x) = x³ - 3x ⋅ x² = x³ - 3x³ = -2x³ ⇒

\begin{cases} x > 0 \Rightarrow f(x, x) < 0 \\ x < 0 \Rightarrow f(x, x) > 0 \end{cases}

2.0.2. Cosa ci dicono queste direzioni?

In alcune direzioni (es. $y = 0$), la funzione crescente da 0
In altre (es. $y = x$), la funzione decrescente da 0
In altre ancora (es. $x = 0$), rimane costante

Questo cambio di segno del valore della funzione nei dintorni del punto ci dice che il punto non può essere né massimo né minimo, bensì un:

✅ Punto di sella

2.0.3. In sintesi

Hai visto i cammini:

$y = 0$
$x = 0$
$y = x$

perché:

La Hessiana non basta a classificare il punto
L'analisi lungo direzioni (o "curve") ci mostra il comportamento locale della funzione
Se il segno della funzione cambia lungo traiettorie diverse → sella

Analisi 2 - Studio delle funzioni in \(R^2\)

Table of Contents

1. Studio di Funzioni in \(\mathbb{R}^2\)