Analisi 2 - Domini normali in \(R^3\)
Table of Contents
1. Definizione
Un dominio normale in \(\mathbb{R}^3\) è un insieme \(E \subset \mathbb{R}^3\) in cui una variabile può essere espressa con limiti dipendenti dalle altre due, e queste due variabili hanno a loro volta limiti indipendenti.
In pratica, possiamo “*proiettare*” \(E\) su un piano e vedere che lungo la direzione di una delle variabili (\(x\), \(y\) o \(z\)) il dominio è semplicemente descritto da due superfici che fanno da “tetto” e “pavimento” (o frontiera anteriore/posteriore ecc.). —
2. Tre tipi di normalità
In \(\mathbb{R}^3\) possiamo avere:
2.1. Normale rispetto a \(z\):
\[ E = \{(x,y,z) \mid (x,y) \in D,\ \varphi_1(x,y) \le z \le \varphi_2(x,y)\} \]
dove \(D\) è la proiezione di \(E\) sul piano \(xy\).
2.2. Normale rispetto a \(y\):
\[ E = \{(x,y,z) \mid (x,z) \in D,\ \psi_1(x,z) \le y \le \psi_2(x,z)\} \]
2.3. Normale rispetto a \(x\):
\[ E = \{(x,y,z) \mid (y,z) \in D,\ \chi_1(y,z) \le x \le \chi_2(y,z)\} \]
3. Vantaggi
Se un dominio è normale rispetto a una variabile, il triplo integrale si può impostare facilmente, scegliendo come variabile più interna quella “normale”:
\[ \iiint_E f(x,y,z)\,dV = \iint_D \left[ \int_{\text{inferiore}}^{\text{superiore}} f(\dots) \,d(\text{variabile}) \right] d(\text{altre}) \]
4. Esempio — Normale rispetto a \(z\)
Sia \(E\) il solido sotto il paraboloide \(z = 4 - x^2 - y^2\) e sopra il piano \(z = 0\).
4.1. Proiezione \(D\) sul piano \(xy\):
\(x^2 + y^2 \le 4\) (cerchio di raggio \(2\)).
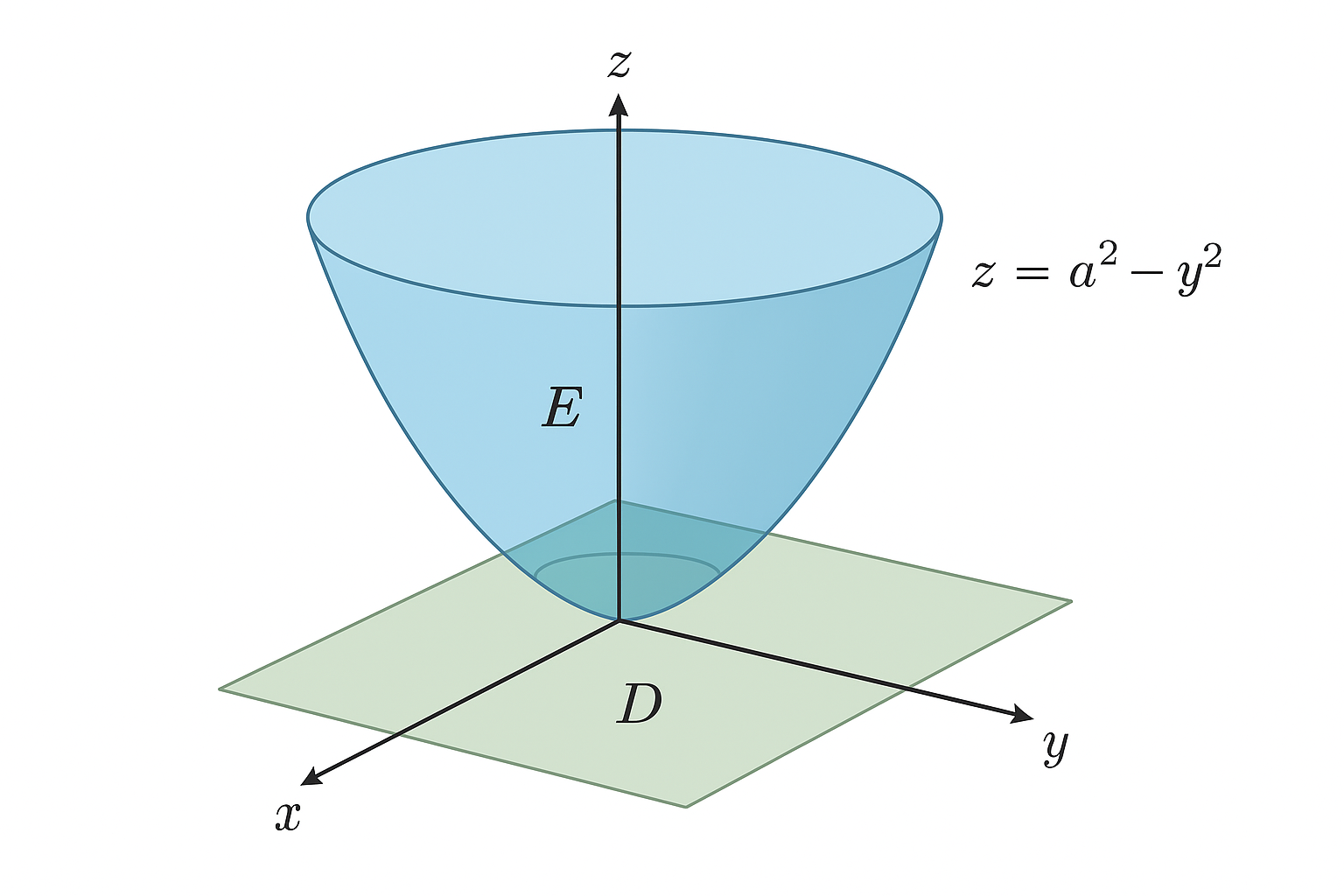
Figure 1: rappresetazione del dominio
4.2. Descrizione:
\[ E = \{(x,y,z) \mid x^2 + y^2 \le 4,\ 0 \le z \le 4 - x^2 - y^2 \}. \]
4.3. Integrale triplo in ordine \(dz\,dy\,dx\):
\[ \iiint_E f(x,y,z) \,dV = \iint_{x^2 + y^2 \le 4} \left( \int_{0}^{4 - x^2 - y^2} f(x,y,z) \, dz \right) dy\,dx. \]
5. Esempio — Normale rispetto a \(y\)
Sia \(E\) il solido limitato da \(y = x^2 + z^2\) e \(y = 4\).
5.1. Proiezione \(D\) sul piano \(xz\):
\(x^2 + z^2 \le 4\) (cerchio raggio \(2\)).
5.2. Descrizione:
\[ E = \{(x,y,z) \mid x^2 + z^2 \le 4,\ x^2 + z^2 \le y \le 4\}. \]
5.3. Integrale triplo in ordine \(dy\,dz\,dx\):
\[ \iiint_E f(x,y,z) \,dV = \iint_{x^2 + z^2 \le 4} \left( \int_{x^2 + z^2}^{4} f(x,y,z) \, dy \right) dz\,dx. \]
6. Esempio — Normale rispetto a \(x\)
Sia \(E\) il solido tra \(x = y^2 + z^2\) e \(x = 9\).
6.1. Proiezione \(D\) sul piano \(yz\):
\(y^2 + z^2 \le 9\).
6.2. Descrizione:
\[ E = \{(x,y,z) \mid y^2 + z^2 \le 9,\ y^2 + z^2 \le x \le 9\}. \]
7. Integrale triplo in ordine \(dx\,dy\,dz\):
\[ \iiint_E f(x,y,z) \,dV = \iint_{y^2 + z^2 \le 9} \left( \int_{y^2 + z^2}^{9} f(x,y,z) \, dx \right) dy\,dz. \]