Sequenze
Table of Contents
- 1. Introduzione
- 2. TDF - Trasformata di Fourier a Tempo Discreto
- 3. Normalizzazione delle TDF
- 4. TDF - Inversione della trasformata
- 5. Convergenza della TDF
- 6. Operazioni tra sequenze
- 7. Sequenze fondamentali
- 8. Proprietà della TDF per sequenze
1. Introduzione
Una sequenza è un insieme di valori discreti \(x(nT)\), anche sostituiti con la notazione \(x[n]\), in cui in ogni campione e' ottenuto dalla relazione in cui \(T_c\) rappresenta il tempo di campionamento e la sua inversa \(f_c = \frac{1}{T_c}\) la frequenza di campionamento mentre \(x_c(t)\) rappresenta il segnale continuo
\begin{equation} \label{org6f20f9d} x[n] = x(t) \delta(t - nT_c) \end{equation}Il segnale continuo puo' essere ricostruito come segue
\begin{equation} \label{eq:10011} \begin{split} x_c(t)= \color{white}\sum_{n=-\infty}^{\infty}x[n] = \color{red}\sum_{n=-\infty}^{\infty}x(t)\delta (t - nT_c)= \color{green} x(t) \sum_{n=-\infty}^{\infty} \delta (t - nT_c) \end{split} \end{equation}2. TDF - Trasformata di Fourier a Tempo Discreto
2.1. Definizione
Nella \eqref{eq:10011} trasformando separatamente i vari membri otteniamo la \eqref{eq:1000} in cui la parte in bianco e' ottenuta applicando la definizione di TDF mentre quella rossa e' ottenuta applicando la proprietà della TDF di un prodotto.
\begin{equation} \label{eq:1000} \begin{split} X_c(f) = \color{white}\int_{-\infty}^{\infty}x_c(t)e^{-j2\pi f t} d_t= \color{white}\int_{-\infty}^{\infty}\sum_{n=-\infty}^{\infty}x[n]e^{-j2\pi f t}=\\ \color{white}\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}x[n]e^{-j2\pi f t}= \color{white}\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}x(nT)\delta(t - nT_c)e^{-j2\pi f t} d_t=\\ \color{white}\sum_{n=-\infty}^{\infty}x(nT)\int_{-\infty}^{\infty}\delta(t - nT_c)e^{-j2\pi f t} d_t= \color{white}\sum_{n=-\infty}^{\infty}x(nT)\int_{-\infty}^{\infty}e^{-j2\pi f nT_c} d_t=\\ \color{white}\sum_{n=-\infty}^{\infty}x(nT)e^{-j2\pi f nT_c} =\\ \color{white}\sum_{n=-\infty}^{\infty}x(nT)e^{-j2\pi n\frac{f}{f_c}} =\\ \color{red} X(f) \otimes f_c\sum_{n=-\infty}^{\infty}\delta (f-nf_c)=f_c\sum_{n=-\infty}^{\infty}X(f - nf_c) \end{split} \end{equation}per cui dalla \eqref{eq:1000} si ha la \eqref{eq:0a}
\begin{equation} \label{eq:0a} \begin{split} X(f)=F[x(t) \sum_{n=-\infty}^{\infty} \delta (t - nT_c)] = \color{red} f_c\sum_{n=-\infty}^{\infty}X(f - nf_c) \end{split} \end{equation}E’ interessante osservare che dal punto di vista matematico Serie di Fourier e TDF sono un notevole caso di dualita' in quanto equivalenti perche' entrambe rappresentano funzioni periodiche ( vds fig 1 ).
Dal punto di vista applicativo invece SDF e TDF sono profondamente diverse perche' la trasformata della prima sono due valori distinti in quanto il segnale e' privo di informazione, cioe' visto un periodo visti tutti, mentre una sequenza discreta di campioni rappresenta delle informazioni che di solito non si ripetono.
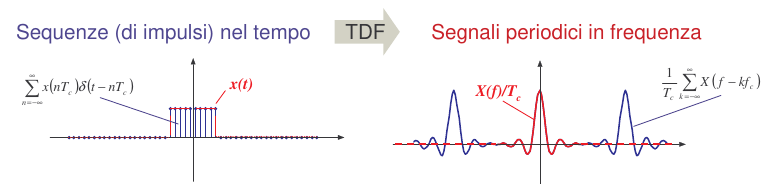
Figure 1: TDF di una sequenza
Da notare che tutte le trasformate di sequenze sono funzioni
periodiche che a differenza di quelle a tempo continuo sono
aperioriche.
3. Normalizzazione delle TDF
Normalizzare la frequenza è utile perché rende la rappresentazione indipendente dalla frequenza di campionamento specifica, facilitando il confronto e l'analisi tra segnali campionati a diverse frequenze. Applicando la seguente sostituzione di variabile
- Frequenza normalizzata : \(F=\frac{f}{f_c}\) da cui \(f=Ff_c\) : rende il periodo della funzione \(X(F)\) unitario con \(F \in [-0.5, 0.5]\).
- Pulsazione normalizzata : \(\omega=2\pi \frac{f}{f_c}=2\pi F\) : rende il periodo della funzione \(X(F)\) di periodo \(2\pi\) con \(\omega \in [-\pi,\pi]\). Da notare che l'intervallo e' lungo \(2 \pi\).
la \eqref{eq:1000} diventa
\begin{equation} \label{eq:1050} X(F)=\sum_{n=-\infty}^{\infty}x[n] e^{-j2\pi nF} \end{equation} \begin{equation} \label{eq:1051} X(\omega)=\sum_{n=-\infty}^{\infty}x[n] e^{-jn\omega } \end{equation}4. TDF - Inversione della trasformata
La struttura della \eqref{eq:1050} e della \eqref{eq:1051} e' quella di una SDF, rispettivamente, di periodo unitario e \(2\pi\) a seconda della normalizzazione e dunque l'inversa della TDF altro non è che il coeficente della SDF. Da notare che il segno dell'esponenziale e' ininfluente.
\begin{equation} \label{eq1100} x[n]=\int_{-0.5}^{0.5} X(F) e^{j2\pi Fn}d_F \end{equation} \begin{equation} \label{eq:1101} x[n]= \frac{1}{2\pi}\int_{-\pi}^{\pi} X(\omega) e^{j\omega n}d_\omega \end{equation}5. Convergenza della TDF
Nella pratica quando si vuole stabilire se una sequenza generatrice di una certa TDF converge si valuta l'assoluta sommabilita' oppure il fatto che il segnale sia ad energia finita.
Per stabilire se un segnale ha una TDF convergente si studia la convergenza dei campioni estrapolati dal segnale.
Per lo studio della convergenza si definisce l'errore di approssimazione inteso come differenza della funzione con la sua somma parziale \(\lim_{M \rightarrow \infty}|X(\omega) - X_M(\omega)|\) in cui :
\begin{equation} \label{eq:1052} X(\omega)= \lim_{M \rightarrow \infty} X_M(\omega)=\lim_{M \rightarrow \infty} \sum_{n=-M}^{M} x[n] e^{j\omega n}=\sum_{n=-\infty}^{\infty} x[n] e^{j\omega n} \end{equation}Si fa notare come \(X(\omega)\) sia la somma infinita di una serie di potenze complesse in cui \(z=e^{-j\omega}\) .
5.1. Convegenza uniforme
E' una convergenza molto forte infatti e questo limita lo studio della TDF alle sole funzioni continue in quanto la \(\sum | x[n]|\) deve essere assolutamente sommabile. Questo tipo di convergenza e' definita come :
\begin{equation} \label{eq:1001 } \begin{split} X(\omega) \leq |X(\omega)|= |\sum_{n=-\infty}^{\infty} x[n] e^{j\omega n}| \leq \sum_{n=-\infty}^{\infty} |x[n]| |e^{j\omega n}| \sum_{n=-\infty}^{\infty} |x[n]| \leq \infty \end{split} \end{equation}che significa per ogni \(\omega \in [-\pi,\pi]\) ( intervallo senza buchi ) \(X(\omega)\) è continua e l'errore si annulla infatti :
\(\forall \ \epsilon > 0 \ \exists \ M_{\epsilon}\) t.c. \(\forall \ M>M_{\epsilon} \ \Rightarrow\) \(|X(\omega) - X_M(\omega)| < \epsilon\)
5.2. convergenza quadratica
Pemette di includere funzioni di TDF con discontinuita' come la \(rect\), cioè segnali ad energia finita ( \(\sum |x[n]|^2 < \infty\) ) . Se io uso la troncata della TDF quello che ottengo in prossimita' della discontinuita' sono delle sovraelongazioni ed aumentando i campioni ottengo una diminuzione del tempo di transizione ma un aumento del valore di picco ( fenomeno di Gibs ) vds fig 2 .
In questo caso si valuta l'errore medio ( uso dell integrale ) nell'intervallo di esistenza della TDF come segue in cui il valore dell'integrale non cambia se in qualche punto la differenza dell'argomento non è nulla ( \(X(\omega)\) discontinua ) e questo spiega perché questo tipo di convergenza è meno stringente :
\(X(\omega) \leq |X(\omega)|^2=|\sum_{n=-\infty}^{\infty} x[n] e^{j\omega n}|^2 \leq \sum_{n=-\infty}^{\infty} |x[n]|^2 \leq \infty\)
\(\lim_{M \rightarrow \infty} \int_{-\pi}^{\pi}|X(\omega) - X_M(\omega)|^2 d_{\omega}=0\)
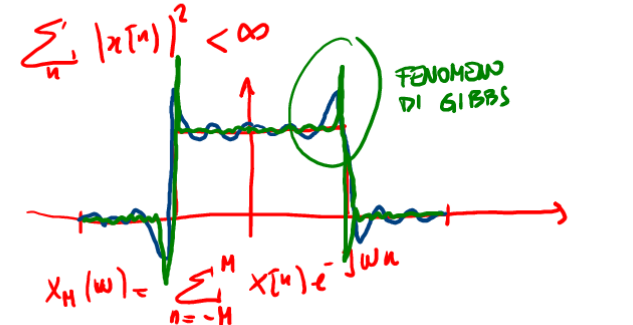
Figure 2: Fenomeno di gibs
5.3. Altri tipi di convergenza
Le due convergenza precedenti non sono sufficienti a garantire la convergenza della TDF di alcune sequenze tipo quella costante di valore unitario \(x[n]=1\). In questo caso come per la SDF e la TDF si introduce la \(\delta[F]\).
6. Operazioni tra sequenze
- Somma \(w[n]=x[n]+y[n]\)
- Prodotto \(w[n]=x[n]y[n]\)
- Covoluzione \(w[n]=x[n] \otimes y[n]=\sum_{k=-\infty}^{\infty} x[k]y[n-k]\)
- Traslazione \(w[n]=x[n-n_0]\)
- Inversione \(w[n]=x[-n]\)
7. Sequenze fondamentali
7.1. Impulso discreto
Da notare che a differenza della \(\delta\) definita per un tempo continuo dove occorre utilizzare le distribuzioni, in ambiente discreto basata solo la seguente definizione :
\begin{equation} \delta(n) = \bigg \{ \begin{array}{l} 1 \ con\ n=0\\ 0 \ per\ tutti\ gli\ altri \\ \end{array} \end{equation}7.1.1. TDF dell'impulso discreto
la quale deve essere vista come la ripetizione del valore 1 nell'intervallo \([-1/2, 1/2]\)
7.2. Funzione sgn[x]
Definizione
\begin{equation} x[n]=sgn[n] =\left\{\begin{matrix}1 & n > 0 \\ 0 & n = 0 \\ -1 & n < 0 \end{matrix}\right. \end{equation}7.2.1. TDF della funzione \(sgn[n]\)
Per la dimostrazione della trasformata discereta della occore definire la seguente funzione il cui andamento è riportato in fig 3
\begin{equation} \label{eq:00101} \begin{split} y[n]=x[n] - x[n-1] = \left\{\begin{matrix}1 & n=[0,1] \\ 0 & altrove \end{matrix}\right. \end{split} \end{equation}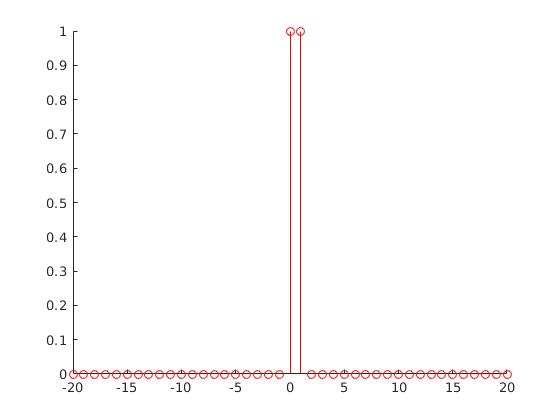
Figure 3: \(x[n]-x[n-1]\)
e trasformata con i seguenti modi :
- usando la proprieta di traslazione tempolare della TDF applicata a \(\delta[n-1]\) ;
- trasformado secondo la definizione di TDF la \eqref{eq:00101};
da cui uguagliando la \eqref{eq:103} e la \eqref{eq:102} ultime due ottengo la trasformata della funzione \(sgn[x]\)
\begin{equation} \label{eq:100005} X(F) = \frac {1 + e^{-j2 \pi F}} {(1 - e^{-j2 \pi F} )} \end{equation}7.3. Gradino unitario
Definizione della funzione :
\begin{equation} \label{eq:1002} u[n]= \bigg \{ \begin{array}{ccc} 1 & n >= 0 \\ 0 & n < 0 \end{array} \end{equation}7.3.1. TDF della funzione a \(u[n]\)
Per il calcolo della TDF e' necessario riscrivere la \eqref{eq:1002} in modo tale da utilizzare relazioni gia' note.
\begin{equation} \label{eq:1010} \begin{split} x[n]=\frac{1}{2}sgn[n]= \left\{\begin{matrix}1/2 & n > 0 \\ 0 & n = 0 \\ -1/2 & n < 0 \end{matrix}\right. \end{split} \end{equation} \begin{equation} \label{eq:10200} \begin{split} y[n]=x[n] + \frac{1}{2} = \left\{\begin{matrix}1 & n > 0 \\ 0 & n \leq 0 \end{matrix}\right. \end{split} \end{equation} \begin{equation} \label{eq:10300} \begin{split} u[n] = y[n] + \frac{1}{2} \delta[n] = \frac{1}{2}sgn[n] + \frac{1}{2} + \frac{1}{2} \delta[n] \end{split} \end{equation}nella \eqref{eq:10300} si aggiunge \(\frac{1}{2} \delta[n]\) in quanto nella \eqref{eq:10200} si vede che in \(0\) vale \(\frac{1}{2}\) infine sommo \(1/2\) alla funzione \(sgn[n]\) per cui ottengo
\begin{equation} u[n]= \frac{1}{2} sgn[n] + \frac{1}{2} + \frac{1}{2}\delta[n] \end{equation}Facendo riferimento alla \eqref{eq:100005} la TDF vale
\begin{equation} U[F]= \frac{1}{2}\frac{1 + e^{-j2\pi F}}{(1 - e^{-j2\pi F})} + \frac{1}{2} \delta[F] + \frac{1}{2} = \\ \frac{1}{1 - e^{-j2\pi F}} + \frac{1}{2}\delta [F ] \end{equation}Da notare che se avessimo applicato la definisione di TDF alla \eqref{eq:1002} avremmo ottenuto la \eqref{eq:10002} mancante della funzione delta che indica che la sequenza orginale ha una parte a frequenza costante per cui la \eqref{eq:10002} è da considerasi errata.
\begin{equation} \label{eq:10002} \begin{split} U(F)=\frac{1}{1 - e^{-j2\pi F}} \end{split} \end{equation}7.4. Esponenziale
Definizione della funzione esponenziale con base reale o complessa :
- Funzione esponenziale bilatera \(x[n]=a^n\);
- Funzione esponenziale unilatera \(x[n]=a^nu[n]\)
7.4.1. TDF della funzione esponenziale unilatera
con \(|a|<1\)
7.5. Esponenziale troncato
Altro modo di scrivere un segnale rettangolare
\(x[n]=a^n[u[n] -u[n-N]]\)
in cui
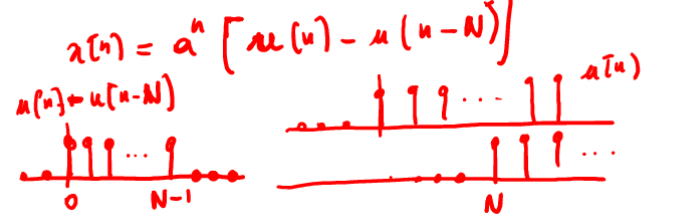
Figure 4: esponenziale troncato
7.5.1. TDF
somma di una serie geometrica troncata e vale \(\forall \ a\).
7.6. Sequenza sinusoidale
\(x[n]=Acos(\omega_0 n + \phi)=\frac{A}{2}e^{j\omega_0 n + \phi} + \frac{A}{2}e^{-j\omega_0 n + \phi}\)
con \(x[n]=x[n+N]\) con \(\omega_0 N=2k\pi, k \in Z\)
8. Proprietà della TDF per sequenze
8.1. linearità
8.2. Traslazione nel tempo
8.3. Traslazione in frequenza
8.4. Inversione Temporale
8.5. Coniugazione
Sia \(x[n]\) allora
\begin{equation} \label{eq:115} \mathfrak{F} { x^c[n] }=X^c(-F) \end{equation}8.5.1. Dimostrazione
8.6. Simmetria
8.6.1. \(x[n]\) reale
- \(x[n]=x^c[n]\);
- \(X(F)=X^c(-F)\);
per cui
- \(|X(F)|=|X^c(-F)|=|X(-F)|\) cioe' \(X(F)\) cioe' il modulo e' pari.
- dalla proprieta' dei numeri complessi in cui se \(a=re^{j\phi}\) allora \(a^c=re^{-j\phi}\) abbiamo che \(\angle X(F)= \angle X^c(-F) = - \angle X(-F)\), cioè la fase e' antisimmetrica;
8.6.2. \(x[n]\) complesso
Tutti i numeri complessi possono essere rappresentati come somma di parte reale e immaginaria in questo modo una sequenza complessa e la sua trasformata possono essere scritte come segue :
- \(x[n]=\mathfrak{Re}(x[n]) + j\mathfrak{Im}(x[n])=x_e[n] + x_o[n]\);
- \(\mathfrak{Re}(x[n])=x_e[n]=\frac{x[n] + x^c[n]}{2} \ \rightarrow \ \mathfrak{Re}(X(F))=X_e(F)\)
- \(\mathfrak{Im}(x[n])=x_o[n]=\frac{x[n] - x^c[n]}{2j} \ \rightarrow \ \mathfrak{Im}(X(F))=\frac{1}{j}X_o(F)\);
- \(X(F)=\mathfrak{Re}(X(F)) + j\mathfrak{Im}(X(F))=X_e(F) + X_o(F)\);
- \(\mathfrak{Re}(X(F))=X_e(F)=\frac{1}{2}X(f) + \frac{1}{2}X^c(F)\)
- \(\mathfrak{Im}(X(F))=\frac{1}{2j}X(f) - \frac{1}{2j}X^c(F) = \frac{1}{j}X_o(F)\);
La parte reale e immaginaria (o dispari e pari) della trasformata di Fourier forniscono una rappresentazione completa della funzione originale in termini di frequenza.
- Parte dispari
- La parte dispari di una funzione reale è sempre una funzione immaginaria pura.
- La parte dispari di una funzione simmetrica è uguale a zero.
- La parte dispari di una funzione antisimmetrica è uguale alla trasformata di Fourier della funzione stessa.
- La parte dispari della trasformata di Fourier può essere utilizzata per ottenere informazioni sulla simmetria della funzione originale. Ad esempio, se la parte dispari è uguale a zero, la funzione originale è simmetrica.
Inoltre, la parte dispari della trasformata di Fourier può essere utilizzata per filtrare le componenti simmetriche di una funzione.
- Parte Pari
- La parte pari di una funzione reale è sempre una funzione reale.
- La parte pari di una funzione simmetrica è uguale alla funzione stessa.
- La parte pari di una funzione antisimmetrica è uguale a zero.
- La parte pari della trasformata di Fourier può essere utilizzata per ottenere informazioni sulla simmetria della funzione originale. Ad esempio, se la parte pari è uguale alla funzione stessa, la funzione originale è simmetrica.
8.7. Derivata in Frequenza
8.8. Covoluzione Discreta
8.9. Prodotto nel Tempo
8.10. Teorema di Parsefal
L'energia della sequenza nel dominio originale si conserva anche nel dominio trasformato.
\begin{equation} \label{eq:19} \begin{split} \sum_{n=-\infty}^{\infty}x[n] y^c[n]=\frac{1}{2\pi}\int_{-\pi}^{\pi}X(\omega)Y^c({\omega}) d_{\omega} \\ \sum_{n=-\infty}^{\infty}|x[n]|^2= \sum_{n=-\infty}^{\infty}x[n]x^c[n]= \frac{1}{2\pi}\int_{-\pi}^{\pi}|X(\omega)|^2d_{\omega} \end{split} \end{equation}che puo' essere interpretata come la ripetizione di periodo \(2\pi\) della densita' spettrale di energia \(|X(\omega)|^2\).