Sistema LTI
Table of Contents
1. Premessa
Si puo' definire sistema l'operatore di trasformazione \(T\) t.c. \(y[n]=T(x[n])\) in cui \(T\) .
- esempio : \(y[n]=(x[n])^2\) non lineare
Fissato un impulso \(n_0\) si definiscono impulsi futuri quelli successivi all'impulso fissato mentre si definiscono impulsi passati quegli impulsi precedenti all'impulso fissato. Vds fig 1
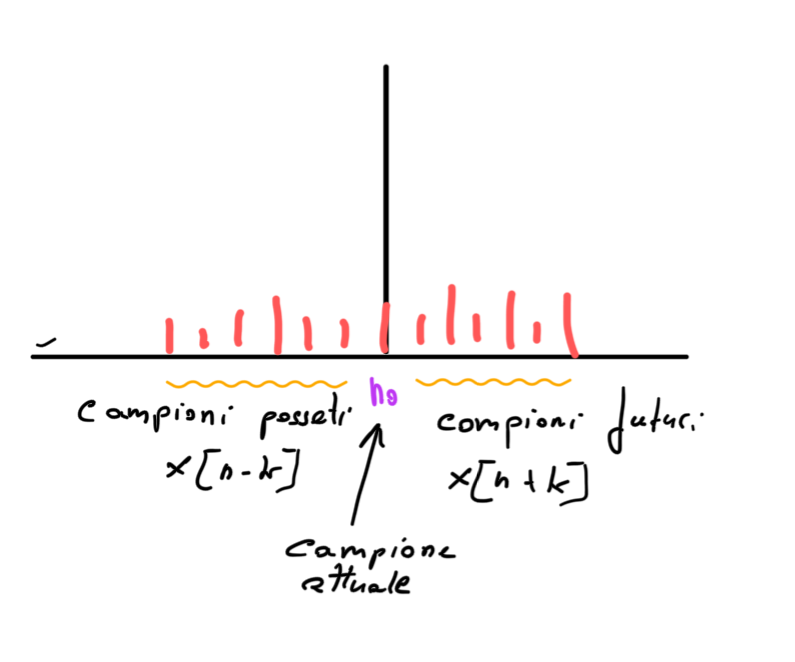
Figure 1: Esempio di sequenze future e passate
1.1. Sistema con memoria
La definizione e' analoga ai sistemi tempo continui detti dispersivi. In questo tipo di sistema la risposta dipende anche dai campioni passati rispetto al campione attuale ed è necessario memorizzare l'intera finestra dei campioni prima di applicarvi la funzione di trasferimento in quanto l'elaborazione inizia da quello più a dx ( ultimo ) e procede a ritroso verso quello attuale.
1.2. Sistema Lineare
Un sistema lineare ha una definizione come quella nella seguente equazione in cui nella risposta compaiono solo addizioni
\begin{equation} \label{eq:1} y[n]=T(a_1x_1[n] + a_2x_2[n])=T(a_1x_1[n]) + T(a_2x_2[n]) \end{equation}esempio di sistema non lineare :
\(y[n]=(x_1[n]+x_2[n])^2=...=x_1^2[n]+x_2^2[n]+2x_1[n]x_2[n]\) in quanto compare una moltiplicazione;
1.3. Sistema Causale
Sistema in cui l'uscita dipende sia dal campione attuale che dai campioni passati, cioe' la risposta impulsiva e' nulla per tutti i termini successi a \(n_0\).
\begin{equation} \label{eq:2} y[n]=\sum_{k=-\infty}^{\infty}h[k]x[n-k] = \sum_{k=0}^{\infty}h[k]x[n-k] \end{equation}1.4. Sistema Reale
Un sistema e' reale quando vengono processati solo i campioni attuali.
1.5. Sistema Tempo Invariante
Sia \(y[n]=T(x[n])\) allora se un sistema è tempo invariante sse \(y[n-n_0]=T(x[n - n_0])\)
Esempio
Nella fig 2 è rappresentata una possibile sequenza d'ingresso in cui se applico un sistema decimatore \(y[n]=x[2n]\) traslando l'ingresso ottengo \(y[n-1]=T(x[2(n-1)])\)
| n | x[n] | x[2n] | x[2(n-1)] |
|---|---|---|---|
| -2 | 1 | 1 | |
| -1 | -1 | -1 | |
| 0 | 1 | 1 | |
| 1 | -1 | -1 | |
| 2 | 1 | 1 | |
| 3 | -1 | -1 | |
| 4 | 1 | 1 |
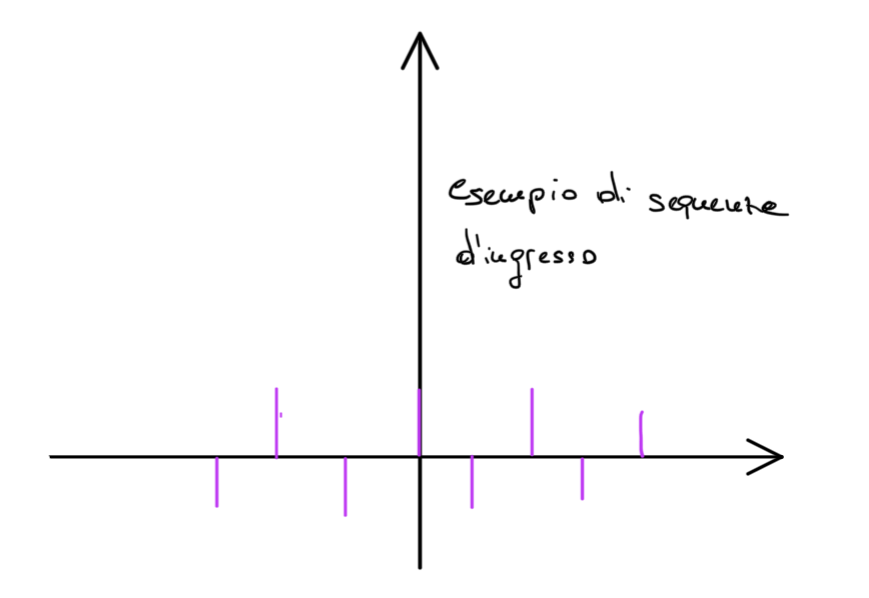
Figure 2: esempio di sequenza di input
1.6. Risposta Impulsiva di un sistema LTI
Caratterizza completamente un sistema.
Oss : Ogni sequenza \(x[n]\) puo' essere vista come somma delle traslazioni del prodotto dell'impulso per il campione corrispondente:
\begin{equation} \label{eq:101} \begin{split} x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]=A_1\delta[n] + A_2\delta[n-1] + A_3\delta[n-2] \end{split} \end{equation}Inoltre sia \(h[n]\) il risultato dell'operatore di trasformazione all'impulso unitario \(h[n]=T(\delta [n])\) e in conseguenza del fatto che il sistema sia tempo invariante \(h[n - k]=T(\delta[n - k])\).
Sia
\begin{equation}\label{eq:3} y[n]=T(x[n])=T(\sum_{k=-\infty}^{\infty}x[h]\delta [n-k]) = \\ \sum_{k=-\infty}^{\infty}x[h]T(\delta [n-k]) = \sum_{k=-\infty}^{\infty}x[h] h[n-k]=x[n]*h[n] \end{equation}NB : l'ultima relazione è un caso particolare dell'equazione alle differenze finite. Inoltre per la proprieta' commutativa dell'operatore di convoluzione si puo' scrivere \(y[n]=h[n]*x[n]\).
1.7. Sistema Stabile
Un sistema e' BIBO ( Boundend input Boundend output ) stabile sse
\(\forall x[n] < M \Rightarrow y[n] < M\)
NB: quando \(h[n]\) è bilatera allora il sistema è stabile in quanto la ROC ( regione anulare ) della sua TDZ contiene il cerchio di raggio unitario.
Ciao dal blocco HTML!
Questo paragrafo è scritto in HTML e verrà esportato come tale.
1.7.1. Teo della stabilità
TEO : CNS affinché un sistema sia stabile e' che \(\sum_{n=-\infty}^{\infty}|h[n]|< \infty\).
NB : se una sequenza è finita la sua TDF è convergente sul cerchio di raggio unitario \(|z|=1\) per cui un criterio di valutazione di stabilità è quello vi verificare se la ROC della TDF di \(h[n]\) contiene il cerchio unitariox.
DIM CS :
TH: \(\sum_{n=-\infty}^{\infty}|h[n]|< M\) \(\rightarrow\) BIBO stabile, cioe' a fronte di un ingresso limitato \(|x[n] < N\) l'uscita e' limitata.
\begin{equation} \label{eq:5} \begin{split} |y[n]|=|\sum_{k=-\infty}^{\infty}h[k]x[n-k]| \leq \sum_{k=-\infty}^{\infty}|h[k]||x[n-k]| \leq MN \end{split} \end{equation}DIM CN :
HP) sistema BIBO stabile
TH) \(h[n]\) assolutamente sommabile \(\rightarrow\) \(\sum_{k=-\infty}^{\infty}|h[k]|
Dimostrazione p.a.
Nego la TH, cioe' a fronte di un ingresso limitato ottengo un uscita illimitata.
Sia \(h[n]\) una sequenza complessa e sia \(x[n]={0,1}\) la sequenza in ingresso ottenuta dalla seguente equazione in cui
il segno - avanti l'indice n serve quando si calcolera' l'uscita per \(n=0\) permettendo di ottenere un prodotto di un numero complesso per il
suo coniugato:
L'uscita del sistema per \(n=0\) e' data da :
abbiamo ottenuto la negazione della tesi contrastando con l'ipotesi.
1.8. Sistemi FIR - IIR
- FIR : sistemi in cui a fronte di un ingresso finito la risposta e' una sequenza finita cioe' hanno una risposta all'impulso \(h[n]\) finita e sono sempre stabili, es : \(h[n]=\delta[n]\);
- IIR : sistemi in cui a fronte di un ingresso finito la risposta e' una sequenza infinita cioe' hanno una risposta all'impulso \(h[n]\) infinita e la stabilita' va verificata di volta in volta in fase di progettazione. Es. \(h[n]=(\frac{1}{2})^nu[n]\);
1.9. Collegamento serie / parallelo
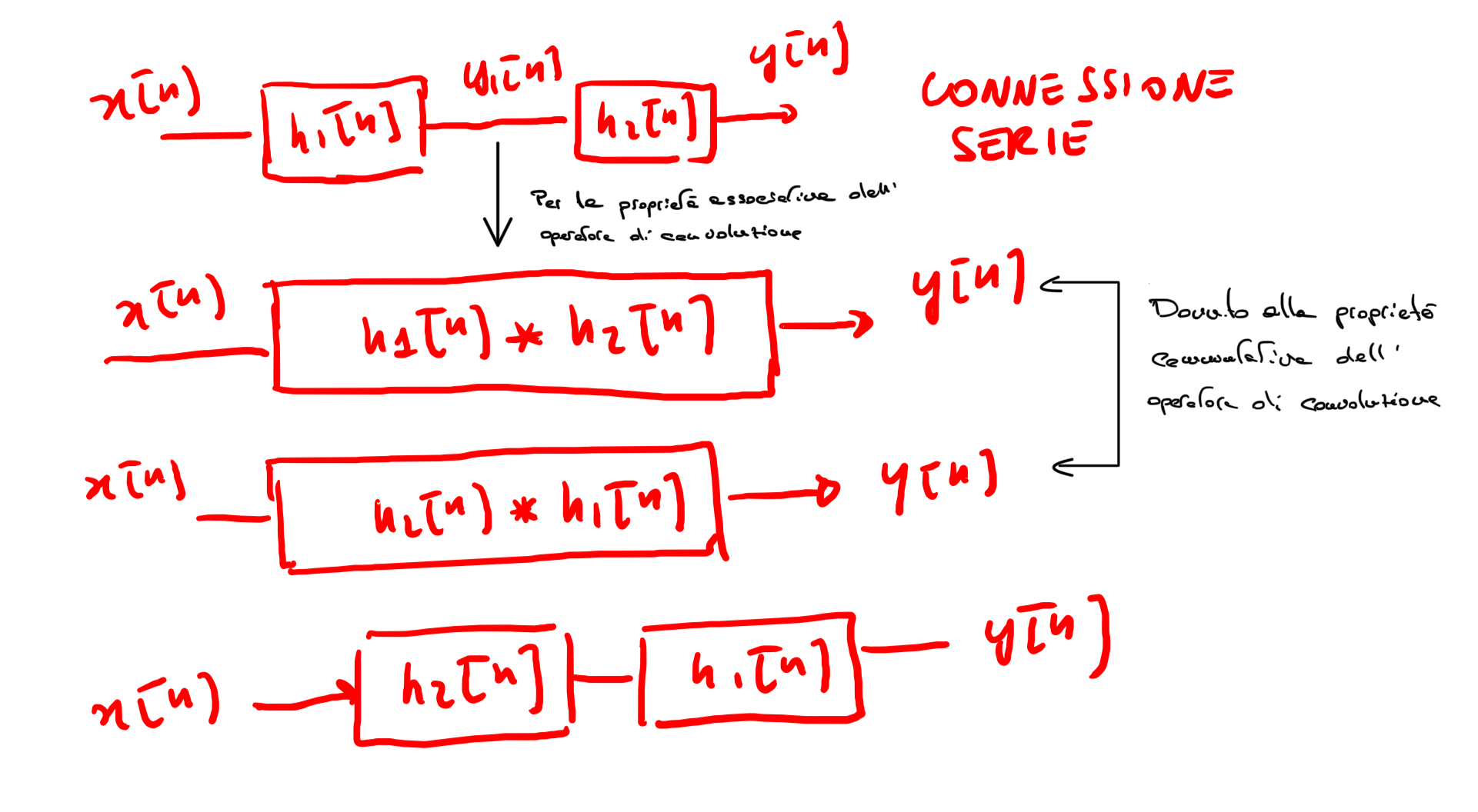
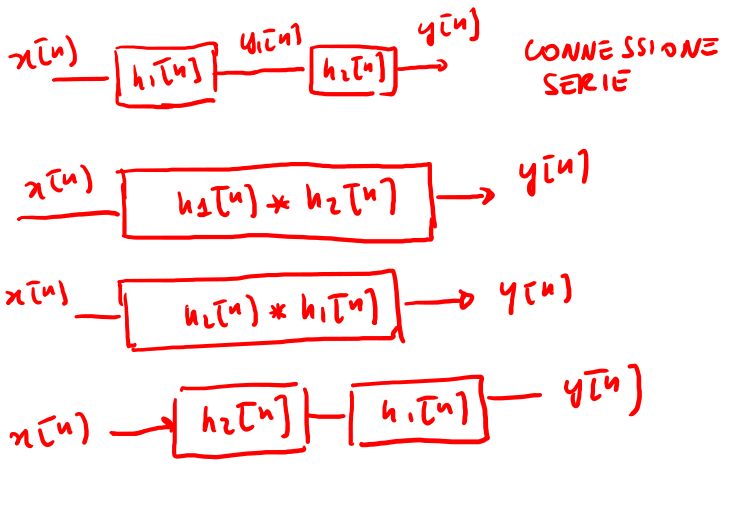
Figure 3: Esempio di collegamento in serie
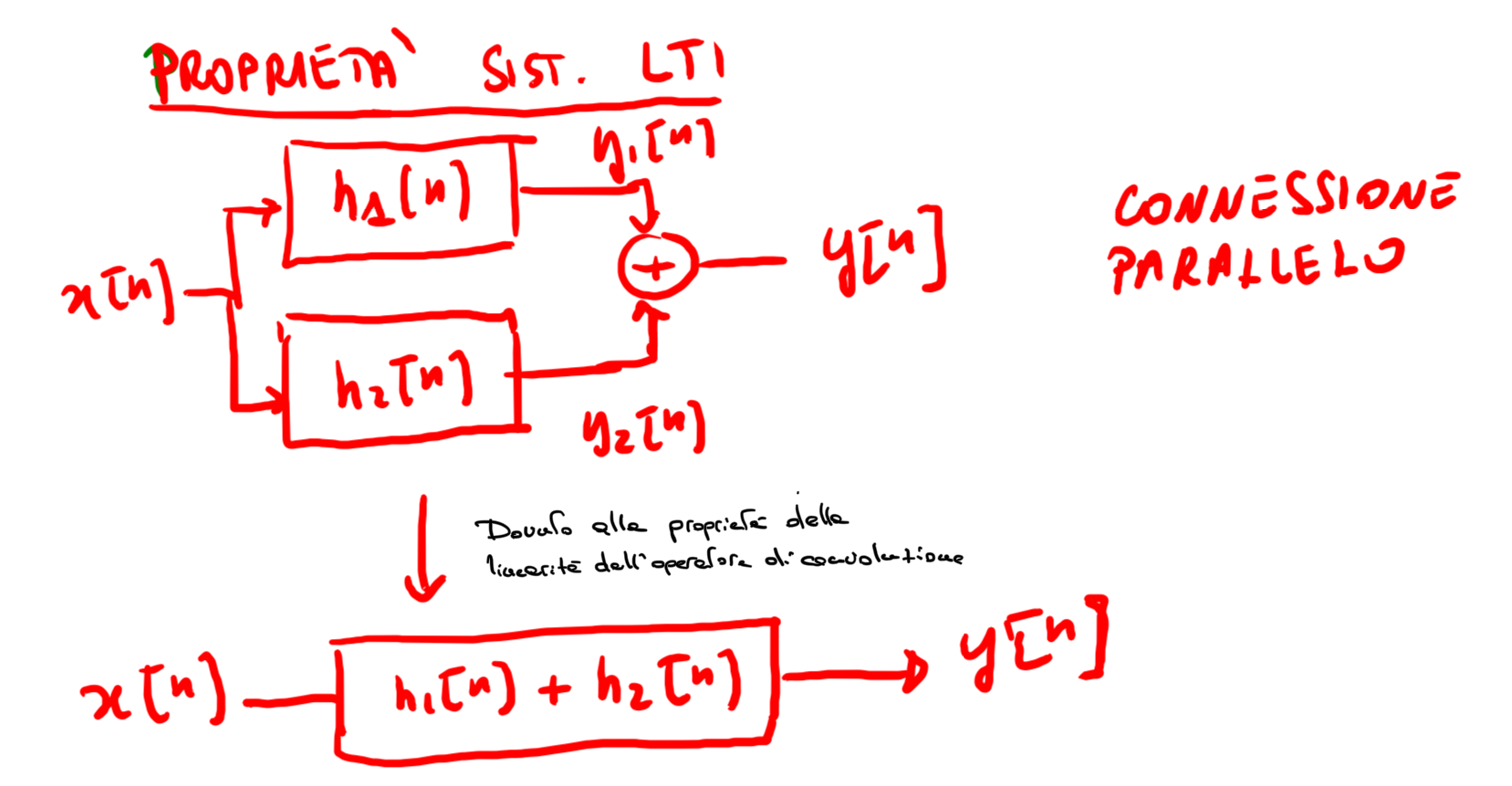
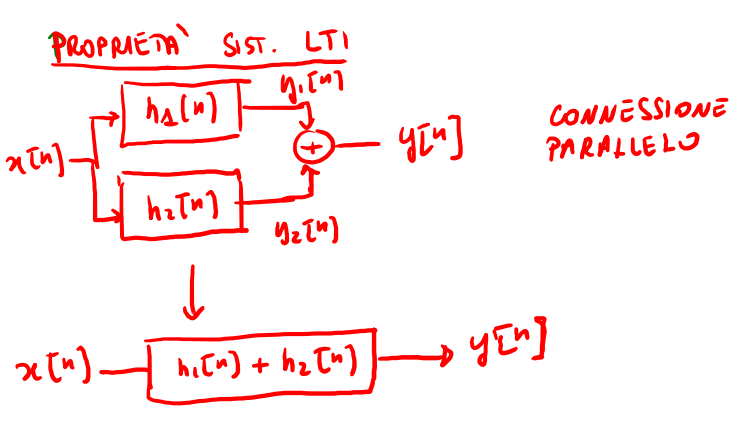
Figure 4: Esempio di collegamento in parallelo
2. Sistemi LTI Elementari
2.1. Ritardatore
Permette di ottenere una versione traslata di \(n_0\) dell'ingresso
Risposta impulsiva : \(h[n]=\delta[n-n_0]\)
\begin{equation} \label{eq:0101} \begin{split} y[n]=\sum_{k=-\infty}^{\infty}h[k]x[n-k]=\sum_{k=-\infty}^{\infty}\delta[k-n_0]x[n-k]=x[n-n_0] \end{split} \end{equation}2.2. Media Mobile
Fa la media di una serie di campioni compresi in una finestra di osservazione composta da \(M\) campioni.
Risposta impulsiva : \(h[n]=\frac{1}{M}\sum_{(limite\ inf)}^{(limite\ sup)}\delta[n-k]\)
Come si nota dalla fig 5 la finestra di osservazione puo' contenere solo campioni passati ( sistemi in tempo reale ) oppure anche campioni futuri ( media ponderata ).
In pratica per ogni finestra di osservazione contenete \(M=a-b\) campioni il sistema LTI produce in output una media degli stessi.
\begin{equation} \label{eq:1010} \begin{split} y[n]=\sum_{k=-\infty}^{\infty}h[k]x[n-k]= \sum_{k=-\infty}^{\infty}(\frac{1}{a-b}\sum_{r=a}^{b}\delta[k-r])x[n-k]=\\ \frac{1}{a-b}\sum_{r=a}^{b}(\sum_{k=-\infty}^{\infty}\delta[k-r]x[n-k])= \frac{1}{a-b}\sum_{r=a}^{b}x[n-r] \end{split} \end{equation}Ad esempio con una finestra di 5 elementi
- media ponderata
| \(a=-\frac{M-1}{2}\) \(b=\frac{M-1}{2}\) | campione |
|---|---|
| -2 | x[n+2] |
| -1 | x[n+1] |
| 0 | x[n] |
| 1 | x[n-1] |
| 2 | x[n-2] |
- media semplice
| \(a=0\) \(b=M-1\) | campione |
|---|---|
| 0 | x[n] |
| 1 | x[n-1] |
| 2 | x[n-2] |
| 3 | x[n-3] |
| 4 | x[n-4] |
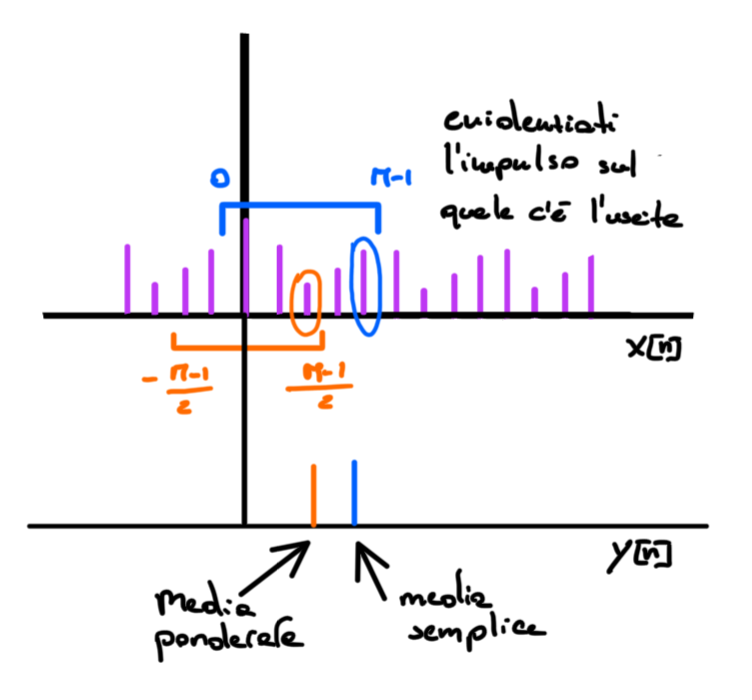
Figure 5: Esempio di struttura della sequenza per media mobile
2.3. Integratore numerico
Esegue la somma dei campioni di n campioni
Risposta impulsiva : \(h[n]=u[n]\)
\begin{equation} \label{eq:1020} \begin{split} y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k]=\sum_{k=-\infty}^{\infty}x[k]u[n-k]= \sum_{k=-\infty}^{n}x[k] \end{split} \end{equation}Come si nota l'integratore e' un integratore di tipo FIR. L'unico modo in cui e' utile questo tipo di circuito e' quando in ingresso vi e' ad esempio un sequenza derivata da un cos campionato in quanto l'alternanza di campioni positivi e negativi fa ottenere una risposta limitata.
2.4. Derivatore numerico
Anche se nonha molto senso parlare di derivata per serie di impulsi in quanto non e' possbile definire il concetto di distanza si puo' comunque simulare tale concetto secondo la seguente relazione \(y[n]=x[n]-x[n-1]\) che applicato alla risposta dell'impulso unitario \(h[n]=\delta[n]-\delta[n-1]\).
3. Implementazione di un sistema LTI
3.0.1. Funzione di Trasferimento
La TDZ della funzione di trasferimento.
\begin{equation} \label{eq:10100} Y(z)=X(z)H(z) \rightarrow \ H(z)=\frac{Y(z)}{X(z)} \end{equation}la cui inversa è :
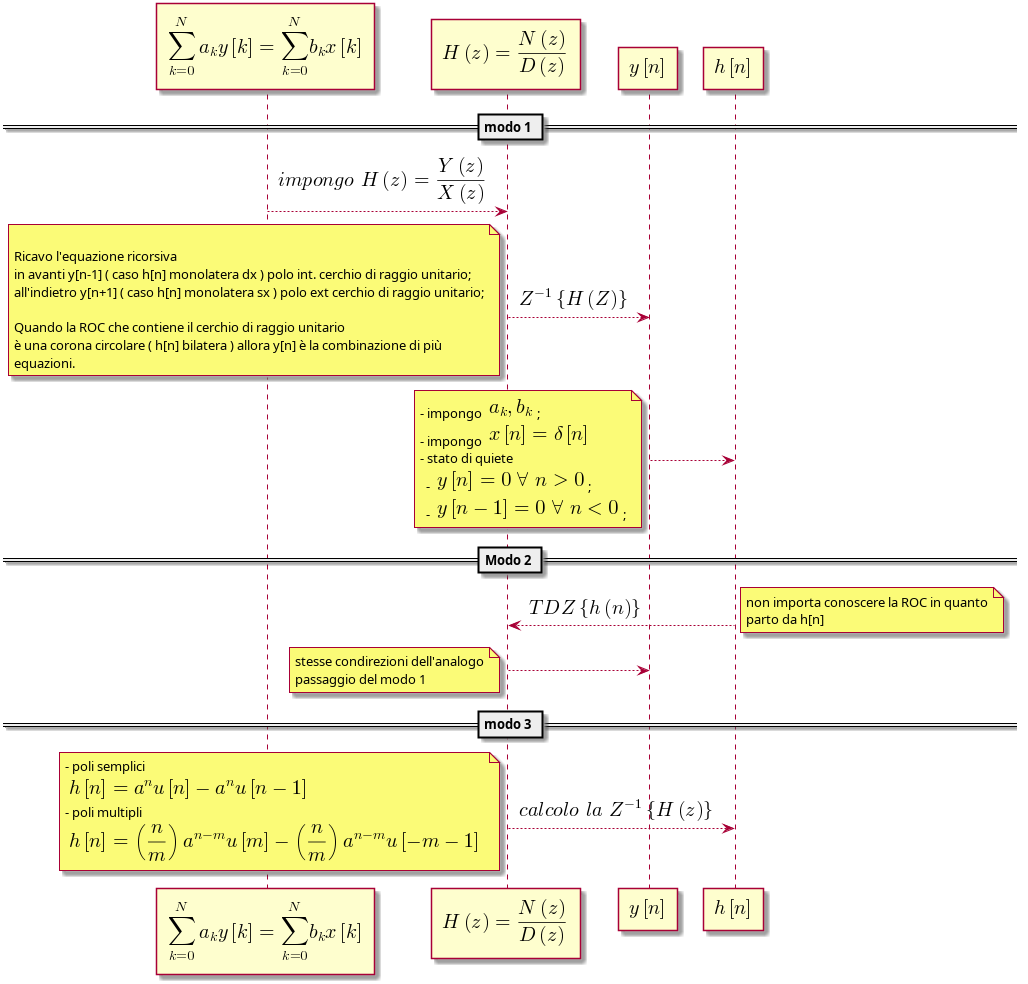
\begin{equation} \label{eq:120} Z^{-1}(H(z))=h[n]= \left\{ \begin{matrix} a^nu[n] - a^nu[n-1] & poli \ semplici \\ \binom{n}{m} a^{n-m}u[m] - \binom{n}{m} a^{n-m}u[-m-1] & poli \ multipli \end{matrix} \right. \end{equation}in cui ognuna delle equazioni \(h[n]\) è di tipo
- monolatera dx : l'equazione ricorsiva \(y[n]\) è in avanti, sistema reale causale;
- monolatera sx : l'equazione ricorsiva \(y[n]\) è all'indietro, sistema con memoria anti-causale;
bilatera : \(h[n]\) limitata, ROC regione anulare, sistema LTI implementato da due equazioni ricorsive;
La scelta del tipo di equazione ricorsiva per l'implementazione del sistema dipende dalla richiesta di stabilità e nel caso affermativo si sceglie quella la cui TDZ contiene il cerchio di raggio unitario.
3.0.2. Equazione alle differenze finite
Modo più generico possibile di legare IN/OUT definita come :
\begin{equation}\label{eq:100} \sum_{k=0}^{N}a_ky[n-k]=\sum_{k=0}^{M}a_kx[n-k] \end{equation}da cui è possibile ricavare l'equazione ricorsiva \eqref{eq:103} che rappresenta una classe di sistemi IR e la cui esatta determinazione dipende dalle condizioni iniziali :
- \(a_k,b_k\) sono parametri caratteristici di sistema;
- \(n\) è un istante temporale
- \(quiete\) stato iniziale del sistema t.c. \(y[n]=0 \ \forall \ n>0\) quando un sistema è in tempo reale op. \(y[n-1]=0 \ \forall \ n<0\) quando in un sistema è presente una retroazione ( ricorsivo ), cioè quando l'uscita dipende anche dai campioni futuri ( sistemi con memoria ).
Altro modo di rappresentare la funzione di trasferimento è applicare la TDZ alla \eqref{eq:100} per cui
\begin{equation}\label{eq:110} \sum_{k=0}^{N}a_kz^{-1}Y(z)=\sum_{k=0}^{M}a_kz^{-1}X(z) \end{equation}per cui
\begin{equation}\label{eq:111} H(z)=\frac{Y(z)}{X(z)} \end{equation}Per implementare un sistema ricavo dalla \eqref{eq:111} l'equazione ricorsiva in avanti ( caso \(y[n]\) e \(h[n]\) monolatera dx ) op. all'indietro ( caso \(y[n]\) e \(h[n]\) monolatera sx ). Solo nel caso di sistemi FIR i coeficenti dell'eq alle diff. finite coincidono con i coeficenti della risposta impulsiva cioè \(b_k=h[k]\)
Nel caso che la ROC della funzione di trasferimento sia una regione anulare allora occorrono più equazioni ricorsive per l'implementazione.
3.0.3. Risposta in frequenza
Molto importante per la determinazione dei sistemi LTI.
sia \(x[n]=e^{j2\pi F_0 n}\) un segnale tonale applicato in ingresso e sia \(h[n]\) la risposta impulsiva del circuito allora
\(y[n]=x[n]*h[n]\)
altro non è che la TDF della risposta impulsiva calcolata in \(F_0\)
\begin{equation}\label{eq:1001} y[n]=x[n]*h[n]=\sum_{k=-\infty}^{\infty}h[k]x[n-k]=\sum_{k=-\infty}^{\infty}h[k]e^{j2\pi F_0 (n-k)}= \\ e^{j2\pi F_0 n}\sum_{k=-\infty}^{\infty}h[k]e^{-j2\pi F_0 k}= e^{j2\pi F_0 n}H(F_0) \end{equation}che rappresentata in modulo e fase diventa
\begin{equation}\label{eq:1002} y[n]=e^{j2\pi F_0 n}|H(F_0)|e^{j\angle H(F_0)}=|H(F_0)|e^{j(2\pi F_0 n + \angle H(F_0))} \end{equation}che si può interpretare come segue : dato un segnale in ingresso ad un certa frequenza \(F_0\), con questo metodo sono adatti i segnali di durata infinita, l'uscita è data dallo stesso segnale la cui ampiezza è moltiplicata per il modulo della risposta di fase calcolato in \(F_0\) e alla fase va aggiunta quella della risposta in frequenza vds fig 6. Infine lo spettro della risposta di fase è quello riprodotto in fig 7.
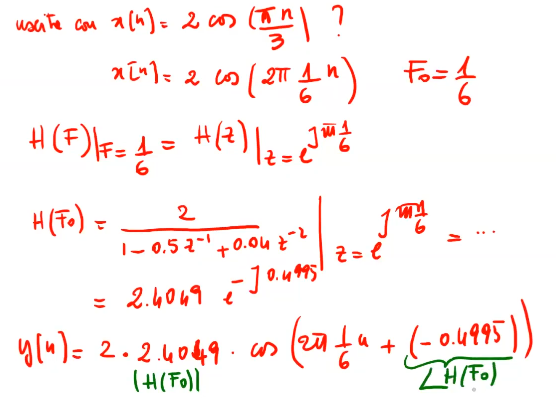
Figure 6: esempio di applicazione della risposta di fase
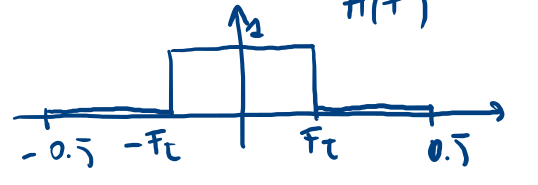
Figure 7: spettro della risposta di fase
Esempio
Esempio di ritardo di fase applicato a sistemi LTI t.d.
Siano \(h_1[n]\) e \(h_2[n]\) due risposte impulsive relative, rispettivamente, ai sistemi di media mobile di cui alle fig 8 e 9 allora come si vede dalla fig 6 il primo può essere visto rispetto al secondo come un sistema LTI che introduce un ritardo di fase di un campione.
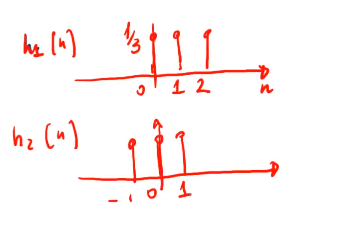
Figure 8: risposta impulsiva di due sist. FIR a media mobile
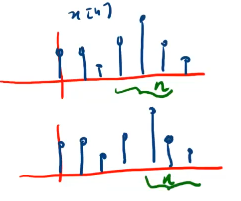
Figure 9: effetto sull'uscita dei due sistemi a media mobile
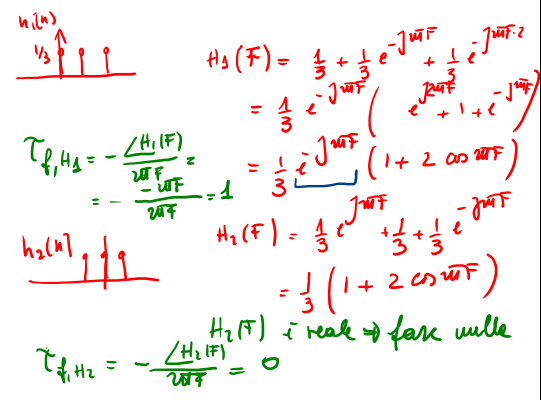
Figure 10: esempio di Risposta in freq per un sistema LTI td
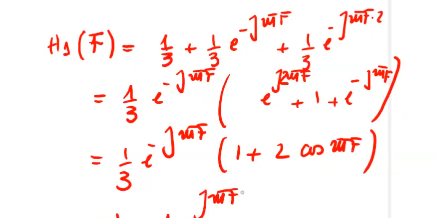
Figure 11: ritardo di fase introdotto dal sistema LTI avente come risposta impulsiva \(h_1[n]\)
3.1. TODO Sistemi non distorcenti in fase - Filtri a fase lineare
Un sistema IR ( poli interni al cerchio di raggio unitario ) si dice che è stabile casualmente quando l'equazione di ricorsione in avanti soddisfa le condizioni di stabilità.
Uno dei sistemi casualmente stabile è quello di seguito indicato il cui ritardo di fase è nullo.
x[n]--->[ H(z) ]-q[n]->[ rev ]-w[n]->[ H(z) ]-e[n]->[ rev ]--->y[n]
- \(Q(z)=X(z)H(z)\)
- \(W(z)=Q(z^{-1})=X(z^{-1})H(z^{-1})\)
- \(E(z)=W(z)H(z)=X(z^{-1})H(z^{-1})H(z)=X(z^{-1})|H(z)|^2\)
- \(Y(z)=E(z^{-1})=X(z)|H(z)|^2\)
da notare che la catena di passaggi è equivalente ad un filtro in cui la risposta in frequenza \(G(z)=H(z)H(z^{-1})=|H(z)|^2\) ha ampiezza reale e fase \(\angle G(z)=0\) per cui se \(|H(z)|^2=1\) allora il filtro non produce un alterazione ne nell'ampiezza ne nel ritardo del segnale in ingresso, per cui se \(H(z)\) producesse un ritardo il filtro in parola lo annullerebbe. Nella pratica però una risposta di ampiezza unitaria non è ottenibile per cui il quadrato del modulo produce un alterazione del segnale in modo non voluto per come progettato \(H(z)\).
Infine la cascata di sistemi a fase lineare sono sempre sistemi a fase lineari vds per esempio la fig. 12. Quello che può cambiare è il tipo di simmetria vds fig 13
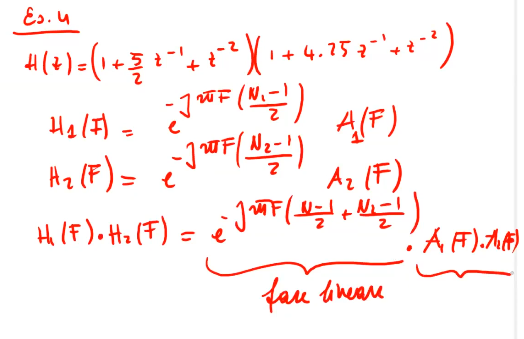
Figure 12: la cascata di due sistemi non cambia la linearità della simmetria.

Figure 13: la cascata di due sistemi non cambia la linearità della simmetria.
- Caratteristiche filtri IR a fase lineare
Si definiscono filtri a fase lineare tutti quei sistemi LTI la cui risposta impulsiva è simmetrica rispetto ad un elemento cardine ( asse di simmetria ) che può essere un impulso ( numero di campioni dispari ) oppure un valore nullo ( numero di campioni pari ).
Si definisce risposta impulsiva simmetrica quella risposta la cui parte dx e sx sono eguali rispetto ad un elemento centrale : simmetria di tipo 1 e 2 ( vds fig 14 ).
Si definisce risposta impulsiva antisimmetrica quella risposta la cui parte dx e sx sono opposte rispetto ad un elemento centrale : simmetria di tipo 3 e 4 ( vds fig 15 ). Nella simmetria di tipo 3 vincolo di campione nullo
Inoltre questo tipo di filtri posso avere una fase nulla dovuta, ad esempio, una simmetria il cui elemento centrale è l'origine. Sistemi con questa tipologia di risposta non sono sistemi casuali perché ci sono campioni negativi.
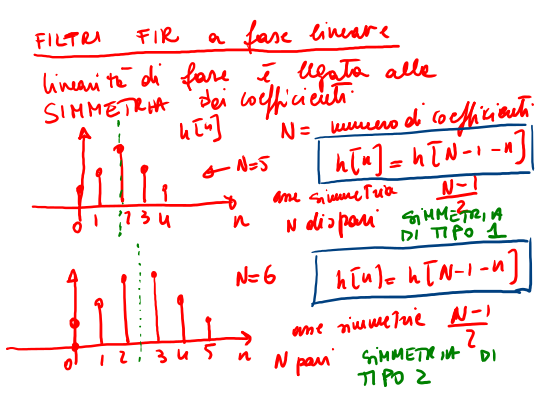
Figure 14: esempi di simmetria tipo 1 e 2
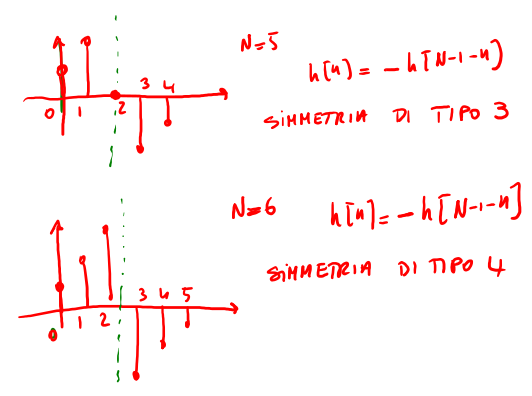
Figure 15: esempi di antisimmetrica tipo 3 e 4
- Studio di H(F) per simmetria di tipo 1
- Numero campioni dispari;
- Come suddividere il treno dei campioni :
- campioni prima del centrale \([0,\frac{(N-1)}{2}-1]\);
- campione centrale \(\frac{(N-1)}{2}\)
- resto dei campioni da quello dopo il centrale a \([\frac{(N-1)}{2}+1, N-1]\)
utilizzando la sostituzione di variabile \(m=N-1 -n\) la \eqref{eq:0001} diventa
\begin{equation}\label{eq:0002} H(F)=\sum_{n=0}^{\frac{N-1}{2} - 1}h[n]e^{-j2\pi Fn}+ h[\frac{(N-1)}{2}]e^{-j2\pi F \frac{(N-1)}{2}} + \sum_{m=0}^{\frac{N-1}{2} - 1}h[m]e^{-j2\pi Fm}=\\ (\sum_{n=0}^{\frac{N-1}{2} - 1}h[n]e^{-j2\pi Fn} + \sum_{m=\frac{N-1}{2} - 1}^{0}h[m]e^{-j2\pi Fm})+ h[\frac{(N-1)}{2}]e^{-j2\pi F \frac{(N-1)}{2}}=\\ (\sum_{n=0}^{\frac{N-1}{2} - 1}h[n]e^{-j2\pi Fn} + \sum_{m=0}^{\frac{N-1}{2} - 1}h[N-1-n]e^{-j2\pi F(N-1-n)})+ h[\frac{(N-1)}{2}]e^{-j2\pi F \frac{(N-1)}{2}}=\\ h[\frac{(N-1)}{2}]e^{-j2\pi F \frac{(N-1)}{2}} + \sum_{m=0}^{\frac{N-1}{2} - 1}h[n](e^{-j2\pi F \frac{(N-1)}{2}} + e^{-j2\pi F (N-1-n)})=\\ e^{-j2\pi F \frac{(N-1)}{2}}(h[\frac{N-1}{2}] + \sum_{n=0}^{\frac{N-1}{2} - 1}2cos(2\pi F (n- \frac{N-1}{2})))=\\ e^{-j2\pi F \frac{(N-1)}{2}}A(F)= e^{-j2\pi F \tau_f}A(F) \end{equation}In pratica in un sistema con \(h[n]\) simmetrica di tipo 1 la TDZ vale
H(F) = fase * termine reale A(F)
in cui è introdotto un ritardo di fase \(\tau_f=\frac{N-1}{2}\)
- Studio di H(F) per simmetria di tipo 2
In modo analogo alla simmetria di tipo 1 sviluppando la \(H(F)\) si ottiene la stessa struttura del tipo indicato ma senza il termine isolato \(h[\frac{N-1}{2}]\) in quanto con N pari il termine medio è nullo.
- Studio di H(F) per simmetria di tipo 3
Procedendo in modo analogo per le simmetrie di tipo 1 e 2 ottengo una \(H(F)=e^{-j2\pi F(\frac{N-1}{2})}jA(F)\) immaginaria pura compreso il termine isolato.
- Studio di H(F) per simmetria di tipo 4
Procedendo in modo analogo per la simmetria di tipo 3 ottengo una \(H(F)=e^{-j2\pi F(\frac{N-1}{2})}jA(F)\) immaginaria pura senza il termine isolato in quanto l'impulso medio è nullo perché i campioni sono pari.
- Studio di H(F) per simmetria di tipo 1
- Filtri IR con fase lineare nulla
Sia \(z_0\) un polo della funzione di trasferimento \(H(z)\) di un generico sistema IR la cui risposta impulsiva è simmetrica rispetto all'origine cioè \(h[n]=h[-n]\) per cui \(H(z)=H(z^{-1})\).
\(H(z_0)=H(\frac{1}{z_0})\)
Se il sistema è stabile \(h[n]\) è bilatera e la ROC della sua funzione di trasferimento è un regione anulare che deve contenere il cerchio di raggio unitario il polo \(z_0\) e il suo reciproco. Dunque i due poli devono essere uno interno al cerchio unitario e l'altro esterno ( vds 16 )
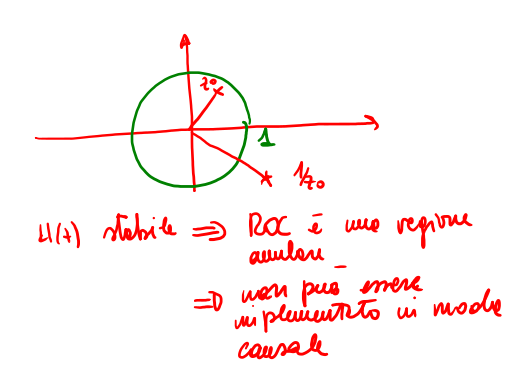
Figure 16: Posizionamento del polo e del suo inverso
3.2. Sistemi non distorcenti in ampiezza - Filtri Passatutto
Un sistema non distorcente in ampiezza è un sistema LTI t.c. \(H(F)=k\) a tutte le frequenze.
Sistemi LTI caratterizzati da una risposta in frequenza del tipo
\begin{equation}\label{eq:9000} H_{ap}(Z)=\frac{a_0 + a_1 z^{-1}+ ... + a_Nz^{-N}}{a_n + a_{N-1}z^{-1} + ... a_Nz^{N}} = \\ \frac{a_0 + a_1 z^{-1}+ ... + a_Nz^{-N}}{z^{-N}(a_0 + a_1z^{-1} + ... a_Nz^{N})}=z^{-N}\frac{A(z)}{A(z^{-1})} \end{equation}in cui ogni termine \(a_i\) è reale. Inoltre
\(H_{ap}(F)=H_{ap}(Z)|_{z=e^{j2\pi F}}=e^{j2\pi F}\frac{A(F)}{A^c(F)}\)
da cui si ottiene
- \(|H_{ap}(F)|=|e^{j2\pi F}||\frac{A(F)}{A^c(F)}|=1\)
- \(\angle H_{ap}(F)=\angle (e^{j2\pi F}\frac{A(F)}{A^c(F)})=2\pi F + - \phi(F) - \phi(F)= 2\pi F - 2\phi(F)\)
3.2.1. Esempio
Nell'esempio di fig 17 e 18 è riportato un esempio di analisi di un filtro all-pass in cui si evidenzia che la scelta del termine reale \(a\) il quale se si avvicina a -1 introduce un ritardo di fase \(2\phi\) molto piccolo in quanto come si vede dall'immagine 17 riducendo l'angolo \(\phi\) di riduce anche la quantità \(2\pi F\)

Figure 17: Esempio di sist LTI del primo ordine
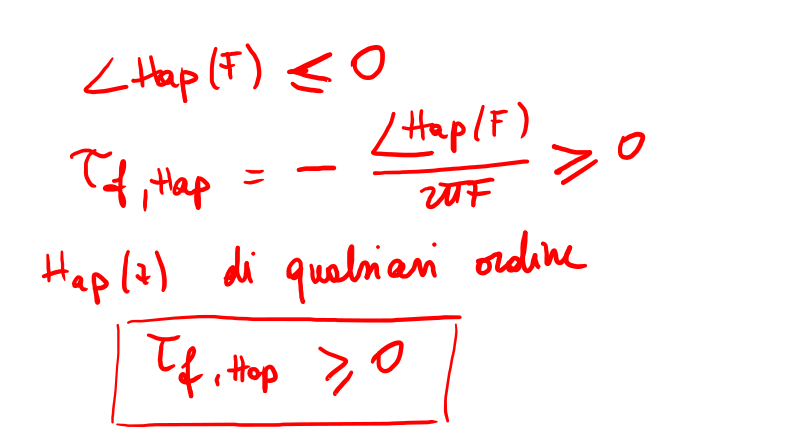
Figure 18: Calcolo della fase di un sistema del primo ordine
3.3. Sistemi a fase minima
I sistemi fa se minima sono tutti quei sistemi in cui i poli sono all'interno del cerchio unitario e il cui ritardo di fase è minore di quello di un sistema analogo avente la stessa funzione di trasferimento.
Quanto mostrato di seguito indica un modo per poter ottenere un sistema a fase minima rispetto ad una funzione di trasferimento relativa ad una risposta impulsiva con simmetria di tipo 1 .
Come si vede le caratteristiche di un sistema a fase minima sono :
- Tutti gli zeri di un sistema a fase minima sono interni al cerchio unitario;
- \(H(z)=H_{min}(z)H_{ap}(z)\) ;
- \(H(F)=H_{min}(F)H_{ap}(F)\) da cui \(|H(F)|=|H_{min}(F)||H_{ap}(F)|=|H_{min}(F)|\);
- L'energia di un sistema a fase minima è concentrata attorno all'origine mentre quella del sistema di partenza è uniformemente distribuita;
- Il ritardo di fase di un sistema all-pass è sempre maggiore o uguale a zero;
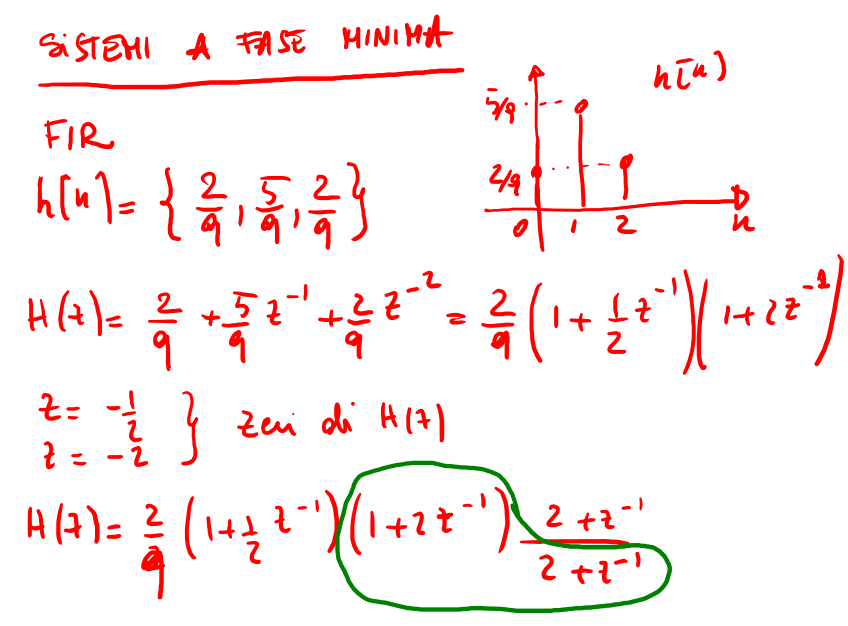
Figure 19: modifica di H(z) di un sistema FIR con simmetria di tipo 1 con zeri interni al cerchio unitario.

Figure 20: Evidenzzazione delle componenti della funzione di trasferimento
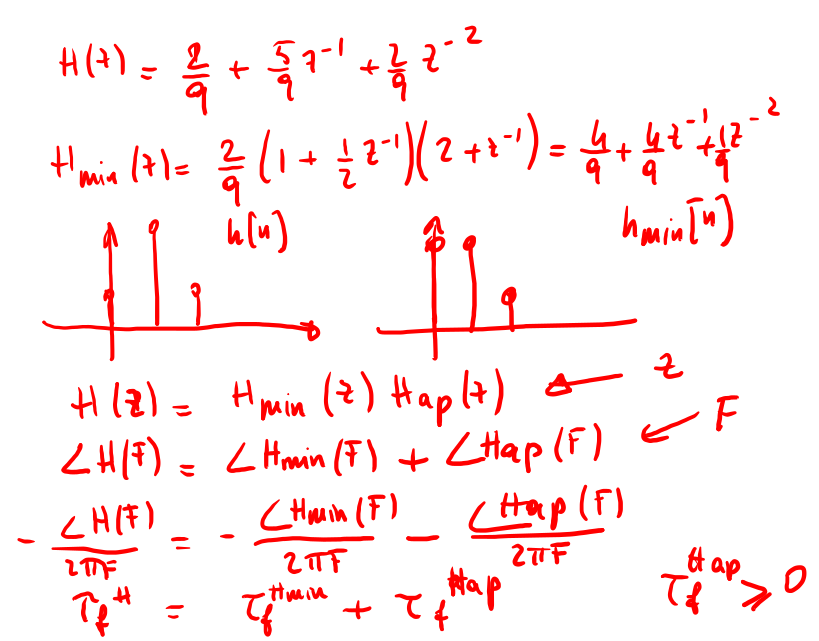
Figure 21: Componenti del ritardo di fase e distribuzione energetica.
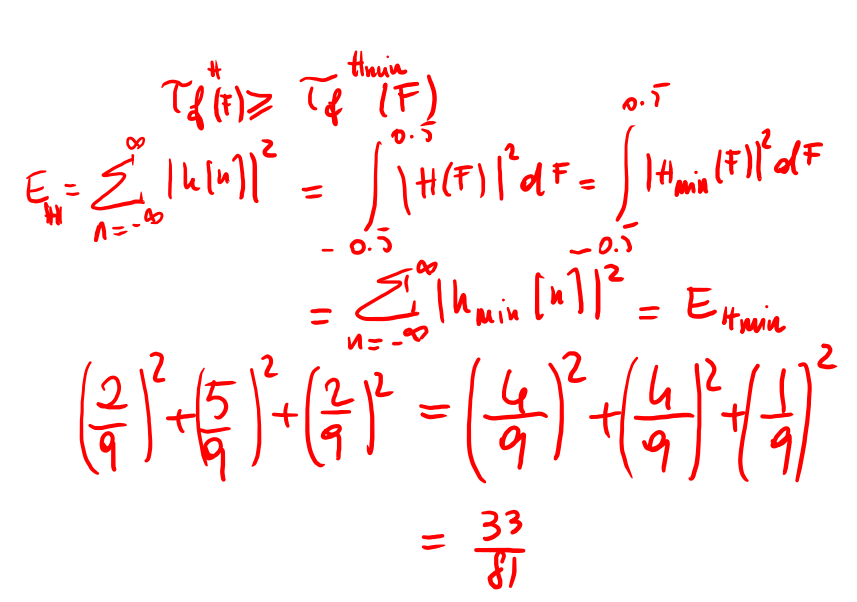
Figure 22: Calcolo della potenza di un sistema a fase minima.
3.4. Calcolo di un sistema