Quantizzazione del segnale campionato
Table of Contents
1. Premessa
Quanto riportato in questo documento e' disponibile per il download al link
2. Introduzione
L’operazione di campionamento trasforma un segnale da tempo-continuo a tempo-discreto.
l’ampiezza dei campioni è, in generale, un numero reale, rappresentabile quindi con un numero infinito di cifre binarie.
L'operazione di quantizzazione e' un operazione non reversibile. L'idea e' quella di associare ad ogni campione \(x[nT]\) un valore numerico \(\hat{x}[nT]=Q[x[nT]]\).
Ogni operazione di campionamento introduce un errore \(e[nT]=\hat{x}[nT] - x[nT]\) funzione dei parametri di quantizzazione: soglia e intervallo.
Infine la scelta dei parametri di quantizzazione e' fatta in funzione dei parametri costruttivi e comunque una sorta di automazione e' l'algoritmo di MAX-Lloyd che calcola la potenza minima dell'errore.
3. Parametri di quantizzazione
- Intervallo di quantizzazione l'intervallo di quantizzazione, detto anche passo di quantizzazione, è la differenza tra due livelli di quantizzazione consecutivi in un processo di quantizzazione di un segnale. In altre parole, è la minima variazione di ampiezza che un segnale può assumere dopo essere stato quantizzato.
- Soglia di Quantizzazione La soglia di quantizzazione è il valore che separa due livelli di quantizzazione consecutivi in un processo di quantizzazione di un segnale. In altre parole, è il valore che determina se un campione del segnale viene quantizzato al livello superiore o inferiore di solito viene preso a metà tra i due livelli.
- Dinamica del quantizzatore è l’ampiezza dell’intervallo di valori rappresentabili dal quantizzatore. Usando B bit, la dinamica del quantizzatore è circa \(2^B\);
- Caratteristica ingresso-uscita rappresenta la funzione \(y = Q(x)\).
- Dinamica del segnale è l’intervallo D di variazione delle
ampiezze dei campioni da quantizzare
- La dinamica del segnale non deve eccedere quella del quantizzatore: in tal caso, valori di ampiezza del segnali elevati non possono essere rappresentati in modo accurato da nessun livello di quantizzazione e viene quindi commesso un notevole errore (overflow );
- La dinamica del segnale, tuttavia, non deve neanche essere troppo inferiore a quella del quantizzatore: in tal caso, infatti, verranno usati un numero ridotto di livelli del quantizzatore e ciò coincide con un numero “effettivo” di bit inferiore a B ;
- In condizioni ideali, la dinamica del segnale è approssimativamente uguale a quella del quantizzatore: in tal caso, le quantità caratteristiche di un quantizzatore (numero di bit B, passo di quantizzazione \(\Delta\), dinamica del segnale D) sono legate dalla relazione \(D= \Delta 2^B\)
3.1. Esempio
Se ho un segnale che varia tra 0 e 10 V che voglio campionare con 4 bit ottengo l'intervallo di campionamento nella rappresentazione {eq:103}
\begin{equation} \label{eq:103} \begin{split} \Delta= \frac{V_{max} - V_{min}}{2^N}= \frac{10}{2^4}=0.625 \end{split} \end{equation}per cui ottengo le seguenti soglie di quantizzazione
- q0 =0 Volt
- q1=0.625 Volt
- q2 =1.25 Volt
- q3 =1.875 Volt
- q4 =2.5 Volt
- q5 =3.125 Volt
- q6 =3.75 Volt
- q7 =4.375 Volt
- q8 =5 Volt
- q9 =5.625 Volt
- q10 =6.25 Volt
- q11 =6.875 Volt
- q12 =7.5 Volt
- q13 =8.125 Volt
- q14 =8.75 Volt
- q15 =9.375 Volt
Se un campione del segnale ha un valore di 0.7 Volt, esso viene quantizzato al livello q1 , con un valore quantizzato di 0.625 Volt. Questo introduce una distorsione di 0.075 Volt nel segnale quantizzato.
4. Quantizzatori uniformi
Una scelta spesso usata, per la sua semplicità, è quella di usare intervalli di quantizzazione aventi tutti la stessa ampiezza \(\Delta\) e livelli di quantizzazione equispaziati tra loro, sempre della quantità \(\Delta\) (quantizzatori uniformi)
La quantità \(\Delta\) viene detta passo di quantizzazione
Il quantizzatore opera per arrotondamento se il livello di quantizzazione coincide con il punto medio dell’intervallo di quantizzazione
Il quantizzatore opera per troncamento se il livello di quantizzazione coincide con la soglia di quantizzazione inferiore.
Il grafico di un quantizzatore a 3 bit è quello indicato in fig. 1
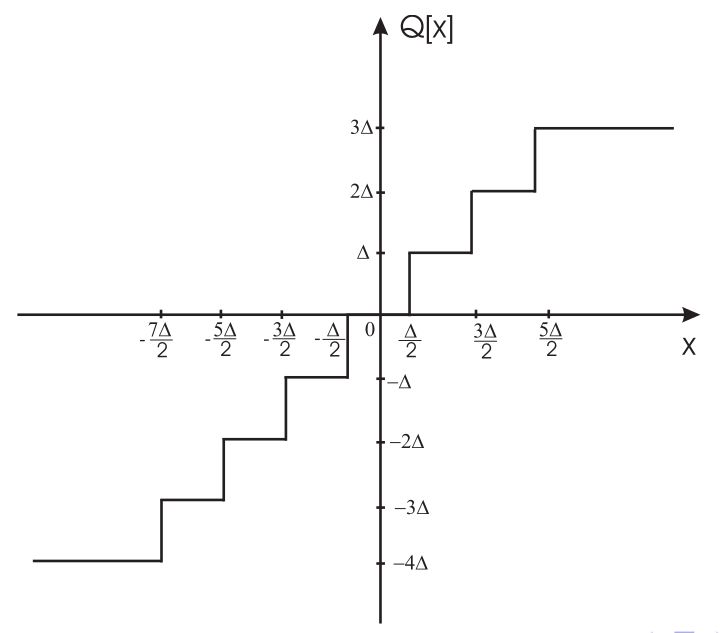
Figure 1: Grafico di un quantizzatore a 3 bit
5. Modello dell'errore
Per determinare le prestazioni di un quantizzatore, l’errore di quantizzazione viene modellato come un processo aleatorio tempo-discreto ciò è utile anche quando il segnale è deterministico (in tal caso, l’errore di quantizzazione sarebbe deterministico)
Il modello dell’errore di quantizzazione usa le seguenti ipotesi
- \(e(nT)\) è un processo stazionario in senso lato (wide sense stationary, WSS);
- la densità di probabilità dell’ampiezza dell’errore di quantizzazione è di tipo uniforme; \(0\leq |e(nT)| \leq \frac{\Delta}{2}\) e questo implica che \(E[e(nT)]=0\) e \(P_e=E[e^2(nT)]=\sigma^2_e=\frac{\Delta^2}{12}\). In cui \(\Delta\) e' il passo di campionamento
- \(e(nT)\) e \(x(nT)\) sono incorrelati per cui \(E(e[nT] x[nT] )= E(e[nT])E(x[nT])=0E(x[nT])=0\)
- i campioni del processo \(e(nT)\) sono incorrelati tra loro dunque .
Nello specifico per la 2) si ha che :
\begin{equation} \label{eq:102} \begin{split} P_e = E[e^2] =\sigma ^2_e = \int e^2 p(e) d_e = \int_{- \Delta / 2}^{\Delta / 2} e^ \frac{1}{\Delta} d_e = \frac{e^3}{3} \frac{1}{\Delta} |_{- \Delta / 2}^{\Delta / 2} = \frac{\Delta ^2}{12} \end{split} \end{equation}La densita spettrale di potenza e' data dalla TDF della \eqref{eq:1023} e' quella indicata nella \eqref{eq:1033} che e' definita nell'intervallo \([-\frac{1}{2},\frac{1}{2}]\) ma che per le proprietà della TDF di sequenze deve essere considerato periodico e dunque e' come dire che la densita' spettrale di potenza e' costante sempre.
\begin{equation} \label{eq:1033} \begin{split} See(F)= \frac{\Delta ^2}{12} \end{split} \end{equation}Inoltre nel caso di quantizzazione per arrotondamento, la densità di probabilità dell’errore di quantizzazione \(e\) (per semplicità, non viene indicato l’indice temporale) è data da:
\begin{equation} \label{eq:101} \begin{split} p_e(e)= \left\{ \begin{matrix} \frac{1}{\Delta} && - \frac{\Delta}{2} < e \leq \frac{\Delta}{2}\\ 0 && altrove \end{matrix} \right. \end{split} \end{equation}6. Indice di qualita' - rapporto segnale rumore \(SNR_{db}\)
Dalla \eqref{eq:101} ne deriva che minore e' l'intervallo di campionamento ( \(\Delta = \frac{D}{2^B}\) ), cioe' maggiore e' il numero di bit di campionamento, minore e' l'errore.
La definizione dell'indice di qualita' ( SNR - signal-to-noise ) ricordando la \eqref{eq:102} e' quella indicata nella \eqref{eq:1043}
\begin{equation} \label{eq:1043} \begin{split} SNR = \frac{S}{P_e}=...=\frac{12S}{D^2} 2^{2B} \end{split} \end{equation}Utilizzando i logaritmi la \eqref{eq:1043} diventa come la \eqref{eq:1053} che come si vede e' formata da due parti, la prima dipende dal numero di bit di campionamento mentre la seconda dipende dalle caratteristiche del segnale
\begin{equation} \label{eq:1053} \begin{split} SNR_{db}=10\log_{0}{SNR}=10 log_{10} \frac{12S}{D^2}2^{2B}=...=6.02B + 10 log_{10}\frac{12S}{D^2} \end{split} \end{equation}6.1. Scelta della dinamica
Per un campionamento ideale la dinamica del segnale dovrebbe coincidere con la dinamica del quantizzatore e per tale motivo e' necessario farlo precedere da un adattatore il quale dovrebbe adattare automaticamente le due dinamiche.
x(t)+r(t) |\ x'(t)+r'(t) +----------+ x[nT]+r[nT]+e[nT]
____________| \_______________| |________
| / | |
SNRi |/ SNRi' +----------+ SNRout = SNRi' + SNRe
G Q ^
|
+------ rumore del quantizzatore
in cui :
- \(SNR_i = \frac{E[x(t)^2]}{E[r(t)^2]}\);
- \(SNR^{'}_i = \frac{E\{[Gx(t)]^2\}} {E\{[Gr(t)]^2\}} = \frac{G^2}{G^2}\frac{E[x(t)^2]}{E[r(t)^2]}=SNR_i\). La scalatura non influisce sul rapporto segnale rumore in quanto scala in egual modo sia il segnale che il rumore;
- \(SNR_{out} = \frac{E\{x'[nT]^2\}}{E\{r'[nT]^2\} + E\{e[nT]^2\}}\) in questo modo abbiamo un legame tra tutte le grandezze del sistema
- Per poter utilizzare le specifiche progettuali nella 3) occorre utilizzare l'inverso \(\frac{1}{SNR_{out}}=\frac{E\{r'[nT]^2\}}{E\{x'[nT]^2\}} + \frac{E\{e[nT]^2\}}{E\{x'[nT]^2\}}=\frac{1}{SNR^{'}_{i}} + \frac{1}{SNR_e}\). Da ricordare che stiamo lavorando con gli inversi per cui indipendentemente da quale grandezza della relazione cerchiamo per trovare il valore di questa occorre fare l'inverso di quanto calcolato.
Quando sopra vale sia per segnali deterministici che per segnali aleatori. Nel primo caso se il segnale ha una dinamica di 6 \(Vpp\) e la si vuole adattare alla dinamica di un quantizzatore standard con dinamica \([-1,1]\) per cui \(D=2\) allora \(G=1/3\). Se invece abbiamo un segnale aletaorio la cui distribuzione e' di tipo gaussiano e con dinamica \([8\sigma_x]\) allora \(G=\frac{1}{4 \sigma_x}\) per cui \(D=2\).
Altra scelta che deve essere fatta in funzione del segnale e' la potenza \(E[x^2(t)]\) che nel caso di tipo sinusoidale con dinamica \(A\) vale \(\frac{A^2}{2}\) mentre per segnali con distribuzione gaussiana vale \(\sigma^2\).
6.2. Potenza dell'errore/rumore
Nel caso di quantizzatore standard con dinamica \(D=2\) la potenza dell'errore \(P_e=E[e^2[nT]]=\frac{2^{-2B}}{3}\) mentre per il rumore del segnale o ne conosciamo la dinamica oppure il rapporto \(SNR_{db}\).
7. Esempi
7.1. Segnale Analogici
Sia