Teorema del Campionamento
Table of Contents
1. Teorema del campionamento
Questa parte descrive le condizioni generali di campionamento e di ricostruzione indipendentemente dai metodi utilizzati.
1.1. Definizioni
- Insieme dei campioni : e' l'insieme \(x_c={x(nT): n \in Z}\) equispaziati nel tempo in cui T e' il passo di campionamento e la sua inversa \(f_c=1/T\) e' nota come frequenza di campionamento. Da notare che il segnale associato all'insieme dei campioni e' continuo in quanto e' nella variabile t che e' continua.
- B banda del segnale;
- 2B frequenza di Nyquist, cioe' la minima frequenza per cui vale il teorema di campionamento;
- segnale a banda limitata : un segnale la cui TDF e' nulla al di fuori dell'intervallo [-B/2, B/2];
- Aliasing fenomeno di sovrapposizioni degli spettri di un segnale. Si verifica quando la frequenza di campionamento e' minore di quella di Nyquist;
1.2. Enunciato del Teorema
- Sia \(x(t)\) un segnale analogico a banda limitata;
- Sia \(f_c\) tc \(f_c > 2B\)
allora
\(x(t)\) puo' essere ricostruito dall'insieme dei campioni \({x(nT): n \in Z}\).
1.2.1. Prima parte della dimostrazione
In questa prima parte si dimostra l' esistenza della TDF dell insieme dei campioni.
Sia \(p(t)=\sum_{n-\infty}^{\infty}\delta(t - nT)\) la funzione pettine di Dirac la quale puo' essere vista come la periodicizzazione della delta di Dirac nell'intervallo base [-T/2, T/2]. Se la \(p(t)\) e che puo' essere espressa come SDF
\begin{equation} \label{eq:104} \begin{split} p(t)= \sum_{n=-\infty}^{\infty} c_k e^{j2\pi n \frac{1}{T}t} \end{split} \end{equation}in cui \(c_k\) vale
\begin{equation} \label{eq:105} \begin{split} c_k = \frac{1}{T}\int_{- T/2}^{T/2} p(t) e^{-j2\pi n \frac{1}{T}t} d_t= \frac{1}{T}\int_{- T/2}^{T/2} \delta(t) e^{-j2\pi n \frac{1}{T}t} d_t = \frac{1}{T}\int_{- T/2}^{T/2} 1 d_t = \frac{1}{T} = f_c \end{split} \end{equation}per cui la \eqref{eq:104} diventa
\begin{equation} \label{eq:106} \begin{split} p(t)= \sum_{n=-\infty}^{\infty} c_k e^{j2\pi n \frac{1}{T}t}= f_c \sum_{n=-\infty}^{\infty} e^{j2\pi n f_c t} \end{split} \end{equation}Sia
\begin{equation} \label{eq:103} \begin{split} x_c(t)=x(t)\sum_{n=-\infty}^{\infty}\delta (t-nT)= \sum_{n=-\infty}^{\infty}x(t)\delta (t-nT)= \sum_{n=-\infty}^{\infty}x(nT)\delta (t-nT) \end{split} \end{equation}che considerando la \eqref{eq:106} diventa
\begin{equation} \label{eq:107} \begin{split} x_c(t)= f_c (\sum_{n=-\infty}^{\infty} e^{j2\pi n f_c t}) x(t)= f_c (\sum_{n=-\infty}^{\infty} x(t) e^{j2\pi n f_c t}) \end{split} \end{equation}in cui \(x_c(t)\) e' una funzione continua in quanto lo e' la variabile \(t\). La TDF di \(x_c(f)\) diventa
\begin{equation} \label{eq:108} \begin{split} X(f) = \mathfrak{F}[ f_c ( \sum_{n=-\infty}^{\infty} x(t) e^{j2\pi n f_c t})]= f_c \sum_{n=-\infty}^{\infty} \mathfrak{F}[ x(t) e^{j2\pi n f_c t} ] = f_c \sum_{n=-\infty}^{\infty}X(f - f_c) \end{split} \end{equation}1.2.2. Seconda parte della dimostrazione
Come si vede confrontanto la fig 1 e la fig 2 se non viene rispettata la condizione di Nyquist gli spettri si sovrappongono e la ricostruzione avviene in modo distorto nelle parti in cui si sovrappongono.
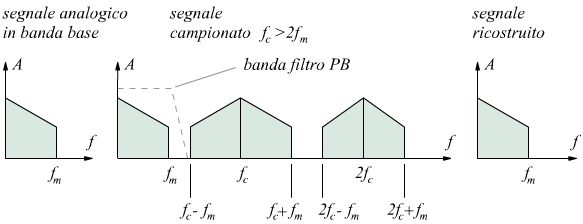
Figure 1: Esempio di TDF si segnale analogico in cui \(f_c > 2B\)
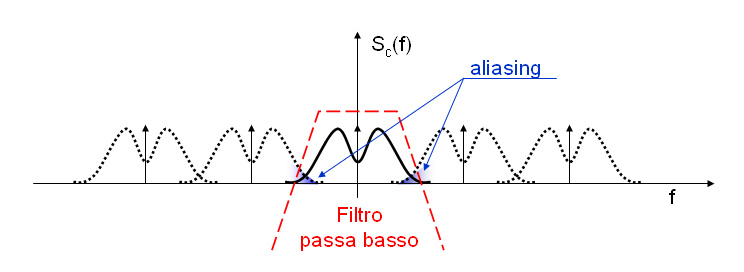
Figure 2: Esempio di aliasing
Tutti i segnali reali hanno banda infinita per cui il fenomeno di aliasing e' inevitabile e nei sistemi reali per far in modo che sia rispetta la condizione n. 1 si introduce, prima del campionamento un filtro di aliasing i cui effetti sono mostrati in fig 3 . In pratica si decide di limitare la banda nell'ipotesi che agli estremi non vi sia contenuto informativo.
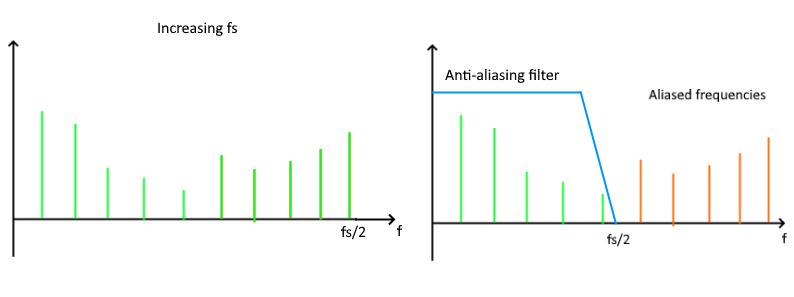 x
x
2. Ricostruzione
2.0.1. Introduzione
Per eseguire la ricostruzione del segnale utilizzo un filtro la cui risposta in frequenza e quella rappresentata in fig 3 la quale e' espressa in modo analitico dalla \eqref{eq:101} che antitrasformata rappresenta la risposta impulsiva del filtro, vds \eqref{eq:102}. Nella risposta in frequenza si nota che vi e' il fattore moltiplicativo \(1/f_c\) in quanto e' necessario compensare il fattore moltiplicativo \(f_c\) che si introduce quando si calcola la TDF del segnale \(x_c(t)\).
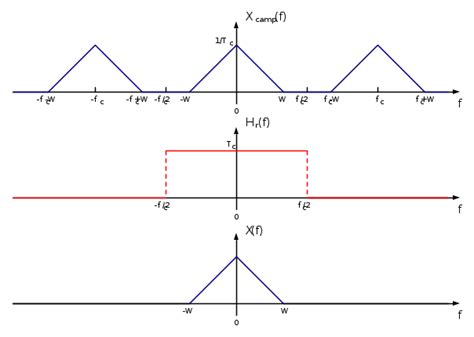
Figure 3: Esempio di risposta in frequenza di un filtro per la ricostruzione
Il grafico della \eqref{eq:102} e' riportato in fig. 4 ove sono evidenziati i punti in cui si annulla che non sono altro che multipli della frequenza di campionamento.
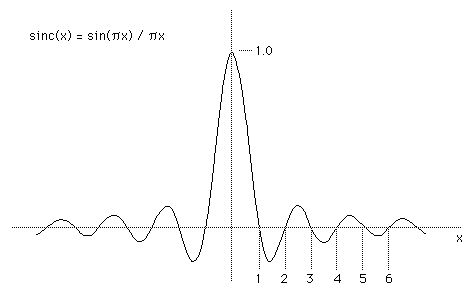
Figure 4: Grafico della funzione \(sinc(\pi f_c t)\)
2.0.2. Come ricostruire il segnale
Nel dominio del tempo io dispongo del segnale \(x_c(t)\) da applicare all' ingresso del filtro per la ricostruzione la cui risposta impulsiva e' \(\hat{x}(t)\) e dunque il segnale ricostruito e' esprimibile come
\begin{equation} \label{eq:1103} \begin{split} \hat{x}(t)=x_c(t)*h_r{t}= [\sum_{n=-\infty}^{\infty}x(nT)\delta (t-nT)]*h_r(t)= \sum_{n=-\infty}^{\infty}x(nT)\delta (t-nT)*h_r(t)=\\k \sum_{n=-\infty}^{\infty}x(nT)h_r(t-nT) = \sum_{n=-\infty}^{\infty}x(nT) \frac{sin[\pi f_c (t - nT)]}{[\pi f_c (t - nT)]} \end{split} \end{equation}Da notare che moltiplicare per la risposta impulsiva permette di passare dalla sequenza \(x(nT)\) al segnale analogico \(\hat{x}(t)\).
L' immagine di cui alla fig 5 mostra come e' possibile ricostruitre un segnale il quale nei punti multipli della frequenza di campionamento l'ampiezza del segnale ricostruito coincide con il vertice della sinc centrata in quel punto mentre in quelli intermedi il valore del segnale e' dato dalla somma di tutte le sinc ma l'apporto maggiore e' dato dalle sinc piu' vicine. Dall'immagine seguente si nota come il numero dei campioni sia direttamente collegato al numero delle sinc e dunque alla precisione della ricostruzione.
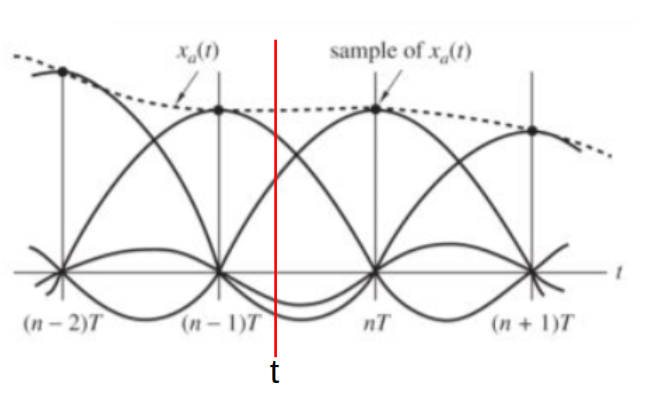
Figure 5: Esempio di ricostruzione del segnale
2.0.3. Implementazione Pratica
Lo schema seguente mostra come si ricostruisce un segnale campionato e quantizzato \(x(nT)\). Non potendo ottenere un impulso di dirac nei circuiti reali viene utlizzato, ad esempio, una scarica di un condensatore su di una resistenza ed anche se introduce una distorsione si puo' compensare con alcuni accorgimenti progettuali.
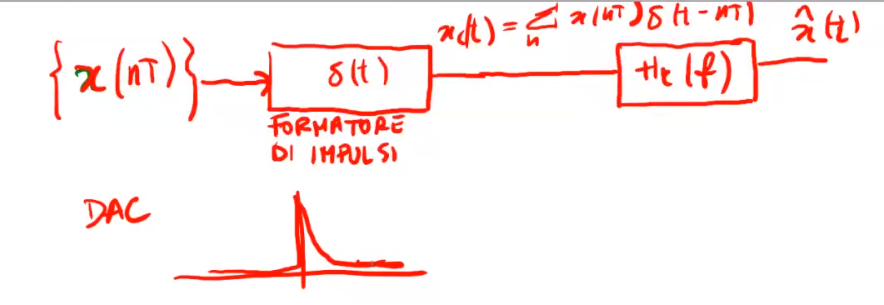
Figure 6: Schema di un circuito DAC
3. Campionamento DOWN-Convertation
E un metodo di campionamento di un segnale passabanda Un segnale passa-banda, con spettro nell’intervallo (f1, f2), avente larghezza di banda B, con B = f2 − f1 , può essere campionato in assenza di aliasing se la frequenza di campionamento \(f_c\) soddisfa le seguenti condizioni:
\begin{equation} \label{eq:1010} \begin{split} \left\{ \begin{matrix} k \frac{f_c}{2} \leq f_1 \\ (k+1) \frac{f_c}{2} \geq f_2 \\ f_c \geq B \end{matrix} \right. \end{split} \end{equation}le cui soluzioni sono ( per k= non ci sono soluzioni ) e la frequenza minima e' 220 che rispetta la condizione di Nyquist.
\begin{equation} \label{eq:0101} \begin{split} k=1 \ \Rightarrow 330 \leq f_c \leq 480 \end{split} \end{equation} \begin{equation} \label{eq:01010} \begin{split} k=2 \ \Rightarrow 220 \leq f_c \leq 240 \end{split} \end{equation}Nel grafico seguente e' riportato il grafico del segnale e delle sue repliche con due diverse frequenze di campionamento.
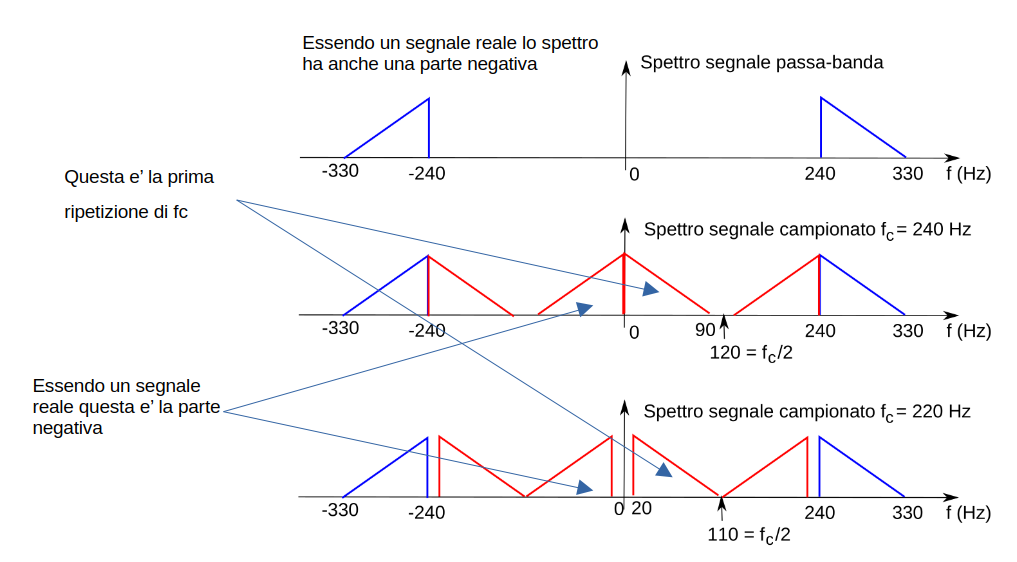
Figure 7: Spettro del segnale e dei suoi campionamenti
4. Campionamento in fase e quadratura
Il tutto si basa sulla teoria dell'inviluppo complesso ( vds frame 1 ) la quale prevede la separazione della parte positiva ( segnale analitico ) di un segnale reale passa banda e poi la sua traslazione in banda base ( demodulazione ).
La rappresentazione di un segnale passa-banda ( modulato ) mediante componenti in fase e quadratura del corrispondente segnale in banda base \(\tilde{x}(t)\) ( segnale demodulato ) permette di ottenere un suo campionamento con il numero minimo di campioni, cioè 2B campioni al secondo, dove B è la banda del segnale.
Con questo metodo le informazioni di interesse trasportate dal segnale (trasmesso o ricevuto) sono contenute nei segnali complessi in banda base, per cui l’estrazione di informazione o la stima di parametri avviene elaborando tali segnali.
4.1. Metodo pratico
La prima parte del seguente schema mostra l'implementazione pratica per ottenere il segnale in fase e quadratura prima del campionamento, mentre la seconda parte mostra come si puo' ricostruire il segnale campionato
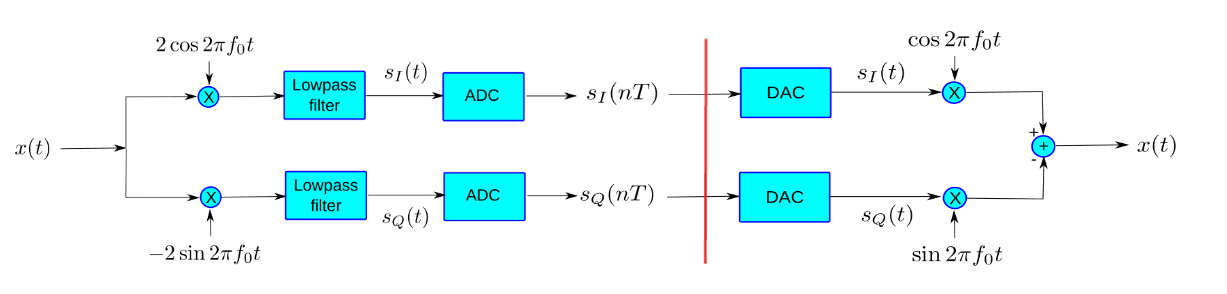
Figure 8: Schema di campionamento e ricostruzione dei segnali in fase e quadratura
- Estrazione della componente in fase di un segnale passa-banda ( modulato ) La \(x_I(t)\) nella \eqref{eq:1029} si ottiene dopo un filtraggio passa-basso
- Estrazione della componente in quadratura dal segnale passa-banda (modulato) in modo analogo a quella in fase (moltiplicando \(x(t)\) per \(−2sin(2\pi f_0 t))\)
Nella seconda parte dello schema dai campioni \(x_I(nT)\) e \(x_Q(nT)\) è possibile ricostruire, mediante convertitori digitale-analogico, i rispettivi segnali analogici \(x_I(t)\) e \(x_Q(t)\) e da questi il segnale passa-banda
5. Campionamento ibrido
Nel campionamento ibrido vi e' l'idea di semplificare il campionamneto in fase e quadratura eliminando tutta le componenti di quel metodo a prezzo pero' di un'aumento della frequenza di campionamento.
Esempio : sia \(x(t)\) un segnale passabanda con la frequenza portante \(f_0=310\) .
Se si prende una frequenza di campionamento \(f_c=4 f_0\) tc \(f_c=1240 \ Mhz\) tc \(T_c = \frac{1}{4 f_0}\) per cui preso \(n \in Z\) abbiamo
\begin{equation} \label{eq:1019} \begin{split} x[nT_c]=x_I[nT_c] cos(2 \pi f_0 \frac{n}{4 f_0}) - x_Q[n T_c]sin(2 \pi f_0 \frac{n}{4 f_0})= \\ x_I[nT_c] cos(\pi f_0 \frac{n}{2 f_0}) - x_Q[n T_c]sin(\pi f_0 \frac{n}{2 f_0}) = \\ \left\{ \begin{matrix} x_I[nT_c] (-1)^{n/2} && n\ pari \\ (-1)^{\frac{n-1}{2}} x_Q[nT_c] && n\ dispari \end{matrix} \right. \end{split} \end{equation}COn questo metodo posso prendere separatamente i campioni in fase e quadratura possono essere presi separatamente, rispettivamente, tra quelli pari e dispari.
Si nota che con la frequenza di campionamento scelta ho 620 campioni in fase e 620 in quadratura.
Si puo' dimostrare che l'ottimizzazione della scelta della frequenza di campionamento puo' essere scelta con la relazione indicata nella \eqref{eq:1025}
\begin{equation} \label{eq:1025} \begin{split} f_c=\frac{4 f_0}{2k+1} \geq 2B \end{split} \end{equation}che nel caso dell'esempio si ha che \(f_c=248\) cioe' 124 campioni in fase e 124 in quadratura.