Appunti Matlab - Sequenze
Table of Contents
1. Argomenti
2. Lezioni
- flie video 04.mp4 minuto 42 file pdf 12 Sequenze Elementari;
- file pdf 11Sequenzeelementari.odf
- file video 06.mp4 minuto 1.59.00 file pdf 13 Processi aleatori;
- file video 07.mp4 inizio video file pdf 12 Campionamento TrasformataFourier
- file video 08.mp4 minuto 1.55.00 file pdf 13 Processi aleatori
- file video 09.mp4 inizio video file pdf 14 quantizzazione
- file video 10.mp4 script matlab
- file video 11.mp4 inizio video file pdf 21 trasformata z
3. Sequenze Elementari
3.1. Impulso unitario
3.1.1. Uso della funzione \(dirac\) di mathlab
N = -20:1:20; x = ( dirac(N-1)); idx = x == Inf; % find Inf x(idx) = 1; % set Inf to finite value stem(N,x); ax = gca; exportgraphics(ax,'./img/dirac.png');
Figure 1: \(\delta[n]\)
3.1.2. Definizione dell'impulso unitario con \(u[n]\)
L'esempio che segue simula l'impulso unitario mediante:
\(\delta[n]=u[n]-u[n-1]\).
Come si vede dal codice è possibile effettuare anche uno shift dell'impulso
\(\delta[n-k]=u[n-k]-u[n-k-1]\)
n=[-20:20]; % si definisce l'intervallo k=10; %% si definisce uno shift verso dx k1=-10; %% shift verso sx x=u(n,k)-u(n-k-1); % definizione del gradino unitario x1=u(n,k1-1)-u(n,k1); % definizione del gradino unitario % [____________|^^^^^^^^^^^^^^^^^^^^^^^^^^^^^] u(n,k-1) % [_____________|^^^^^^^^^^^^^^^^^^^^^^^^^^^^] u(n,k) % [____________|_____________________________] x=u(n,k-1)-u(n,k) figure; % definisce una nuova finestra di plot dove verrano disegnati i plot seguenti hold on; % blocca il riquadro appena creato stem(n,x,'r'); figure; % definisce una nuova finestra di plot dove verrano disegnati i plot seguenti hold on; % blocca il riquadro appena creato stem(n,u(n,k1),'b'); stem(n,u(n,k1-1),'g'); stem(n,x1,'r'); legend('u(n,k1)','u(n,k1-1)','u(n,k1-1)-u(n,k1)'); ax=gca; % associa l'oggetto grafico figure ad una variabile exportgraphics(ax,'./img/du.png');
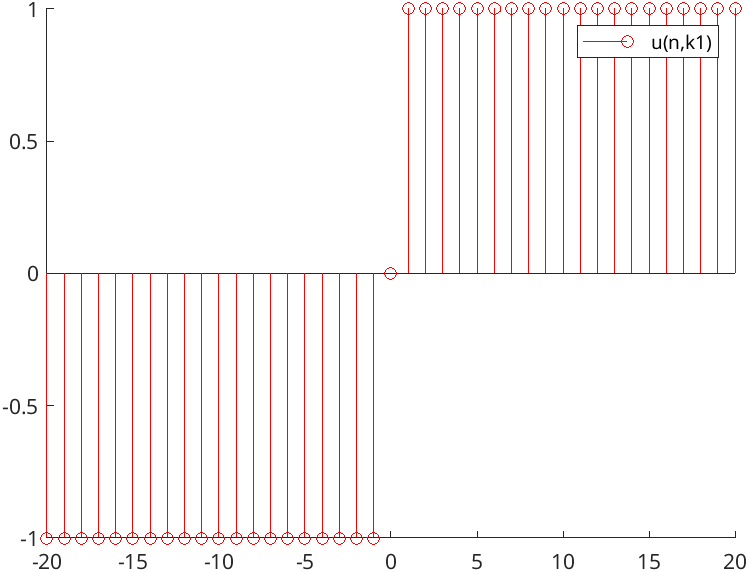
Figure 2: \(u(n,k1-1)-u(n,k1)\)
3.2. Funzione segno
In matlab esiste la funzione sign(x) la quale restituisce 1 o -1 in relazione al segno dei singoli valori dell'array x. Per praticita e' stata definita una funzione segno personalizzata.
3.2.1. sgm - Funzione segno alternativa
% definizione di sgn[n] % La funzione modella il gradino come segue % - u[n] = u(n); % - u[n-k] = u(n,k); % - u[n+k] = u(n,k); % in cui n è l'intervallo di definizione definibile come intervallo rappresentato % % function y=sgm(n,k) if nargin == 1 k=0; end % shift del vettore dell'intervallo n=n+k; % creazione del vettore sgn % find(n<0) trova tutti gli indici con valori negativi % n(.........) trova tutti i valori negativi % (n(.........)<0) crea una array di 1 quanti sono i valori negativi trovati % (................)*-1 se i valori cercati sono quelli negativi si moltiplica l'array precedente per -1 % |<---val negativi-->| 0 |<val positivi>| y=[((n(find(n<0))<0)*-1) 0 (n(find(n>0))>0)]; end
3.2.2. Uso di sign(x) e sgm(m,n)
addpath('./m/'); n=[-20:20]; % si definisce l'intervallo k=-10; % si definisce uno shift verso dx x1=sign(n); % shifth utilizzando la funzione segno x2=sgm(n,k); % utilizzo della funzione personalizzata x3=sgm(n-k); % altro esempio di shift con la funzione personalizzata figure; ax=gca; % associa l'oggetto grafico figure ad una variabile subplot(2,2,1); stem(n, x1,'r'); legend('sign[n]'); subplot(2,2,2); stem(n, x2,'b'); legend('sgm(n,10)'); subplot(2,2,3); stem(n,x3,'g'); legend('sgm(n-10)'); saveas(gcf,'./img/sgm.png');
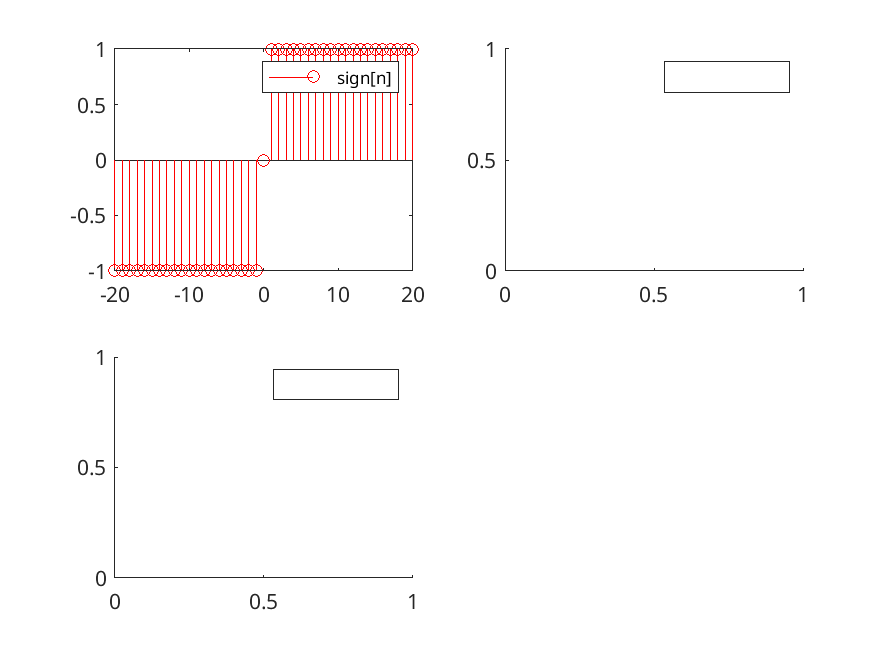
Figure 3: Esempi di utilizzo della funzione segno
3.3. Gradino unitario u[n]
% definizione di u[n] % La funzione modella il gradino come segue % - u[n] = u(n); % - u[n-k] = u(n,k); % - u[n+k] = u(n,k); % in cui n è l'intervallo di definizione definibile come intervallo rappresentato % % function y=u(n,k) if nargin == 1 k=0; end y=[(n-k)>0]; % [------------------------------------------------] n % [..............k.................................] k % [--------------0+++++++++++++++++++++++++++++++++] n-k % [000000000000000111111111111111111111111111111111] test (n-k)>0 end
3.3.1. Esempio
n=[-20:20]; % si definisce l'intervallo k=3; %% si definisce uno shift verso dx k1=-10; %% shift verso sx x=u(n); % definizione del gradino unitario y=u(n,k); % definizione del gradino unitario con shift a dx z=u(n,k1); % definizione del gradino unitario con shift a sx figure; % definisce una nuova finestra di plot dove verrano disegnati i plot seguenti subplot(2,2,1); stem(n,x,'r'); legend('u[n]'); subplot(2,2,2); stem(n,y,'g'); legend('u[n-3]'); subplot(2,2,3); stem(n,(x-y),'b'); legend('u[n]-u[n-3]'); subplot(2,2,4); stem(n,(y-x),'r--'); legend('u[n-3]-u[n]'); saveas(gcf,'./img/u.png');
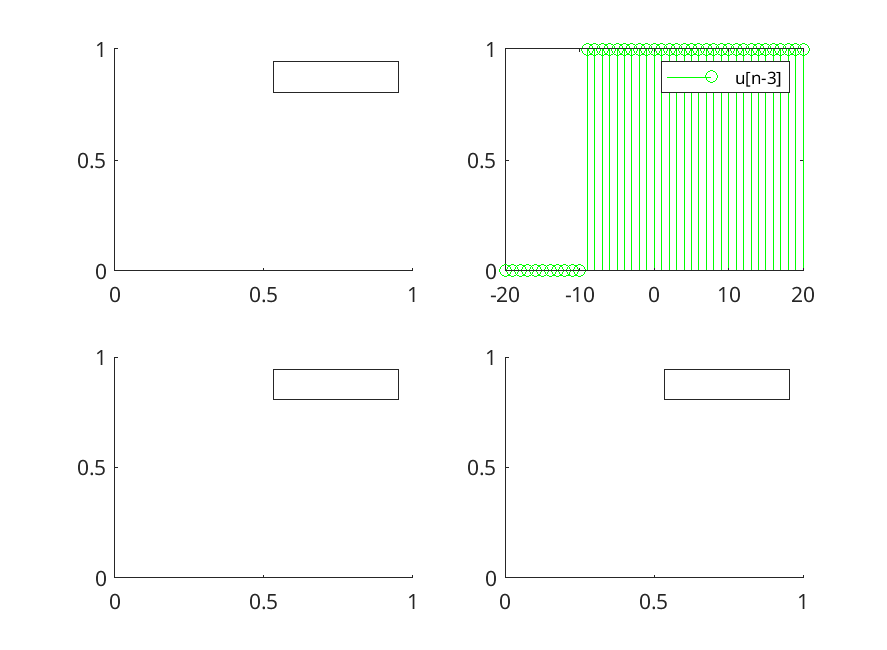
Figure 4: Esempio di plotting della funzione u[n]
3.3.2. Definizione della funzione gradino mediante la funzione segno
n=-20:20; % si definisce l'intervallo k=-10; % si definisce uno shift verso dx y=0.5 * sign(n); y1=y + 0.5; y2=y1 + 0.5*dirac(n); ax=gca; % associa l'oggetto grafico figure ad una variabile figure; subplot(2,2,1); stem(n, y,'r'); legend({'$\frac{1}{2} sign[n]$'}, 'Interpreter','latex'); subplot(2,2,2); stem(n, y1,'b'); legend({'$\frac{1}{2}sign[n] + \frac{1}{2}$'},'Interpreter','latex'); subplot(2,2,3); stem(n, y2,'g'); legend({'$\frac{1}{2}sign[n] + \frac{1}{2} + \frac{1}{2} \delta [n]$'},'Interpreter','latex'); saveas(gcf,'./img/usgm.png');
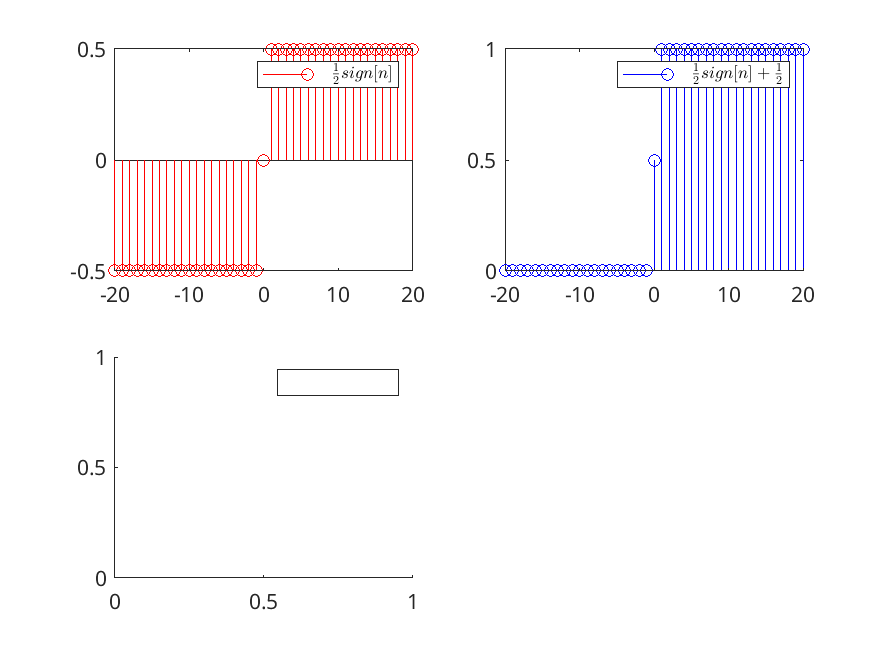
Figure 5: Definizione di \(u[n]\) tramite la funzione \(sgn[n]\)
3.4. Campionamento di sin
3.4.1. sinsignal
La funzione sinsignal campiona un segnale sinusoidale restiuendo il vettore [[valori di sin],[base dei tempi]].
%funzione di campionamento di un segnale sinusoidale % f0: frequenza % phi : fase % A: ampiezza % fc : frequenza di campionamento % N : numero di campioni function [y,t]=sinsignal(f0, phi, A, fc, N) Tc=1/fc; % passo di campionamento t=(0:N-1)*Tc; % base dei tempi - array di valori della grandezza della sin % crea un vettore con i valori assunti dalla funzione sin % in questo modo si simula un campionamento fatto con la delta di D. y=A*sin(2*pi*f0*t + phi); end
3.4.2. Esempio di campionamento
f0=100; A=10; phi=0; fc=2000; N=200; [x,t]=sinsignal(f0,phi,A,fc,N); figure; subplot(2,1,1); stem(t,x); subplot(2,1,2); plot(t,x); saveas(gcf,'./img/sin.png');
Da notare che il massimo contributo lo porta il picco della sinc ma per la ricostruzione esatta e' necessario anche il contributo della coda.
Figure 6: Valori campionati di sin e base dei tempi
3.4.3. Esempio di ricostruzione di campioni
%% sinc_anim_robusto.m clear; close all; clc; %% Parametri f0 = 100; A = 10; phi = 0; fc = 2000; N = 400; T = 1/fc; n = 0:N-1; tc = n*T; x = A*sin(2*pi*f0*tc + phi); %% Tempo denso per animazione durata = N*T; t = 0:1e-4:durata; % passo più grosso per velocità xr = zeros(size(t)); %% Funzione sinc locale mySinc = @(u) arrayfun(@(v) (v==0)*1 + (v~=0)*sin(pi*v)/(pi*v), u); %% Figura figure('Color','w','Renderer','opengl'); hold on; grid on; box on; % plot(t, A*sin(2*pi*f0*t + phi), 'b'); % segnale originale h_xr = plot(t, xr, 'k', 'LineWidth', 1.5); % somma parziale % stem(tc, x, 'filled'); xlim([0 durata]); ylim(1.4*A*[-1 1]); axis manual; shg; %% Loop animazione sinc for k = 0:N-1 s = x(k+1) .* mySinc((t - k*T)/T); h_sinc = plot(t, s, 'r', 'LineWidth', 1); xr = xr + s; set(h_xr,'YData',xr); drawnow limitrate; pause(0.02); % pausa delete(h_sinc); end plot(t, A*sin(2*pi*f0*t + phi), 'b'); % segnale originale
Di seguito l'animazione e' prodotta eseguendo il codice precedente.
3.5. Esponenziale Reale
% La funzione modella a^n % % a = base % N = lunghezza della sequenza % function y=esp(a,N) y = a.^N; end
N = 50; % lunghezza della sequenza a = 0.9; % base reale dell'esponente b = [-20:20]; % si definisce l'intervallo k = 10; % si definisce uno shift verso dx x = esp(a,b); y = u(b,k); z = y.*x; figure; hold on; %subplot(2,2,1); stem(b,x,'b'); %subplot(2,2,2); stem(b,y); %subplot(2,2,3); stem(b,z); legend({'$a^b$','$u[n-10]$','$a^b * u[n-10]$'},'interpreter','latex'); saveas(gcf,'./img/esp.png');
Figure 7: Funzione Esponenziale
3.6. Esponenziale complesso

Figure 8: come rappresentare un exp complesso
N = 50; % lunghezza della sequenza a = 0.9*exp(1j*pi/8); % base complessa b = [-20:20]; % si definisce l'intervallo k = 10; % si definisce uno shift verso dx x = esp(a,b); %y=u(b,k); %z=x.*y; figure; subplot(2,2,1); stem(b,x); label("Exp complesso"); %stem(b,y); %stem(b,z); subplot(2,2,2); stem(b,real(x)); xlabel("Base"); %xlabel("sample"); ylabel("real"); subplot(2,2,3); stem(b,imag(x)); xlabel("base"); ylabel("imaginary"); saveas(gcf,'./img/espc.png');
Figure 9: andamento dell'esponenziale complesso
3.7. Esponenziale invertito
int = [-20:20]; % intervallo dell'esponenziale int_inv = -1.*int; % intervallo invertito base = 2; % base dell'esponenziale exp_inv = base.*int_inv; % esponenziale invertito u1 = u(b,-1); exp_inv_trc = exp_inv.*u1; exp_neg = -1.*exp_inv; u2 = u(int_inv,-1); exp_neg_trc = exp_neg.*u2; figure; subplot(2,2,1); stem(b,exp_inv_trc); legend({'$a^{-n}u[n-1]$'},'interpreter','latex'); subplot(2,2,2); stem(b1,exp_neg_trc); legend({'$-a^{-n}u[-n-1]$'},'interpreter','latex'); saveas(gcf,'./img/espi.png');

Figure 10: andamento dell'esponenziale complesso
4. Esercizi
4.1. Calcolo energia e potenza
Scrivere uno script che calcoli energia e potenza del segnale \(x[n] = cos(2π0.15n)\) con \(n \in \{0, 1, . . . , 49 \}\)
- Input: una sequenza x
- Output: energia E e potenza P della sequenza
n=[-20:20]; % si definisce l'intervallo k=10; %% si definisce uno shift verso dx k1=-10; %% shift verso sx x=u(n-k)-u(n-k-1); % definizione del gradino unitario x1=u(n-k1)-u(n-k1-1); % definizione del gradino unitario figure; % definisce una nuova finestra di plot dove verrano disegnati i plot seguenti hold on; stem(n,x,'r'); stem(n,x1,'g'); saveas(gcf,'./img/es1.png');
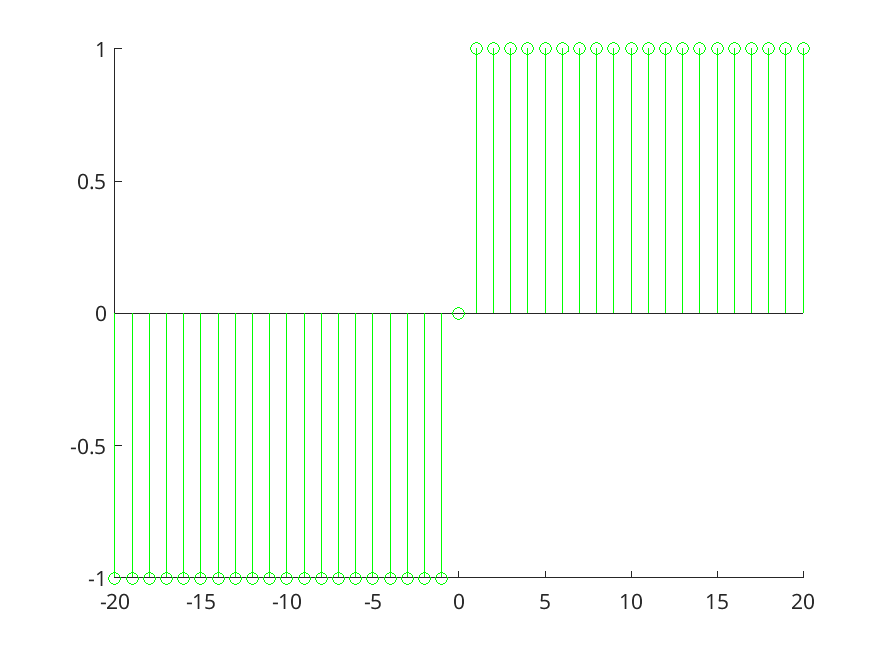
Figure 11: Calcolo energia potenza