Discrete Trasformata di Fourier
Table of Contents
- 1. DFT e IDFT
- 2. Covoluzione Aperiodica ( lineare )
- 3. Covoluzione circolare
- 4. FFT - Fast Fourier Trasform - Implementazione DFT
1. DFT e IDFT
Passaggio da un dominio discreto del tempo ad uno discreto nella frequenza. Analogo della SDF per segnali periodici.
In analogia con la SDF si parla di segnale periodico quando vi è la ripetizione di un insieme di campioni finiti oppure vi è una ripetizione di un sottoinsieme di campioni.
L'utilizzo della DFT è utilizzata per disegnare funzioni in matlab.
Cosa significa ripetizione data una sequenza \(x[n]\) si definisce ripetizione la seguente relazione :
\begin{equation} \label{eq:200} \tilde{x}[n]=\sum_{r=-\infty}^{\infty}x[n+rN] \end{equation}in cui N è la lunghezza della sequenza, cioè il periodo. Se il periodo della ripetizione è maggiore di quello base si aggiungono zeri mentre se il periodo base è un sottoinsieme di una sequenza ottengo una distorsione in quanto non posso più ricavare i campioni del segnale originale.
Le sequenze periodiche di periodo N formano uno spazio lineare \(P_N(C)\) formato sui complessi.
Siano \((\tilde{f},\tilde{g})\) due funzioni periodiche, si definisce prodotto scalare
\begin{equation} \label{eq:201} <\tilde{f},\tilde{g}>=\sum_{n=0}^{N-1}f[n]g^c[n] \end{equation}Sia, ad esempio, \(x[n]\) una sequenza di periodo 4 allora una base ( \(dim(P)=N\) ) dello spazio lineare dove è definita la sequenza è quella di cui alla fig 1 allora si può definire ogni singola ripetizione come :
\begin{equation} \label{eq:202} \tilde{x}[n]=\sum_{k=0}^{N-1}x[k]\tilde{e_k}[n] \end{equation}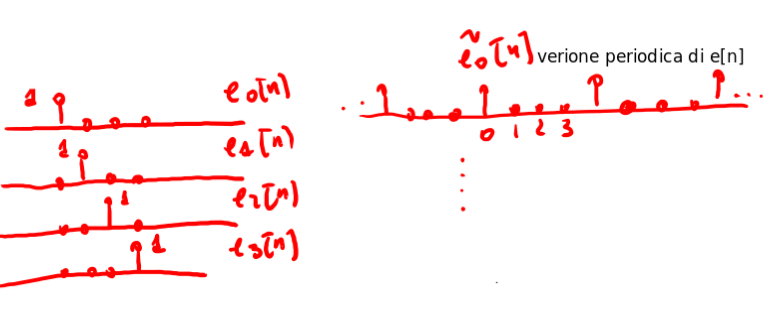
Figure 1: Esempio di base di uno spazio lineare
Per poter operare analiticamente su di uno spazio lineare si definisce ogni singolo elemento della base come segue di modo che sia periodico di periodo N e che sia ortogonale a tutti gli altri elementi della base ( vds \eqref{eq:204} ); :
\begin{equation} \label{eq:203} u_k[n]=\frac{1}{\sqrt{N}}e^{j2\pi k \frac{n}{N}} \end{equation} \begin{equation} \label{eq:204} < u_p , u_q > = \sum_{n=0}^{N-1}u_p u^{*}_{q} = \sum_{n=0}^{N-1} \frac{1}{\sqrt{N}} e^{j2\pi p \frac{n}{N}} \frac{1}{\sqrt{N} } e^{-j2\pi q \frac{n}{N}}= \frac{1}{N} \sum_{n=0}^{N-1} e^{j2\pi (p-q) \frac{n}{N}} = \left\{ \begin{matrix} 1 & p=q \\ 0 & p \neq q \end{matrix} \right. \end{equation}Con una base definita come nella \eqref{eq:203} un segnale periodico di periodo N è ottenibile come
\begin{equation} \label{eq:205} \tilde{x}[n]= \sum_{k=0}^{N-1}<\tilde{x}[n],\tilde{u_k}[n]>\tilde{u_k}[n]= \sum_{k=0}^{N-1} \tilde{X}[k]\tilde{u_k}=\\ \sum_{k=0}^{N-1} \tilde{X}[k]\frac{1}{\sqrt{N}}e^{j2\pi k \frac{n}{N}} \end{equation}che altro non è che la struttura della SDF in cui il coefficiente vale :
\begin{equation} \label{eq:206} \tilde{X}[k]=<\tilde{x}[n],\tilde{u}_k>= \sum_{n=0}^{N-1} \tilde{x}[n]\tilde{u^*_k}[n]= \sum_{n=0}^{N-1} \tilde{x}[n]\frac{1}{\sqrt{N}}e^{-j2\pi n \frac{k}{N}} \end{equation}e assomiglia alla struttura del coefficiente della SDF che può essere visto come la proiezione della sequenza periodica lungo un elemento della base ( elemento trigonometrico ad una specifica frequenza \(F=k/N\) ) e che a meno del termine \(\frac{1}{\sqrt{N}}\) ( introdotto affinché ogni elemento della base sia ortogonale agli altri ) coincide con la TDF della sequenza \(x[n]\) calcolata nel punto \(\frac{k}{N}\) per cui riscrivendo la \eqref{eq:206} come :
\begin{equation} \label{eq:210} X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi n \frac{k}{N}}= \sum_{n=0}^{N-1} x[n]e^{-j2\pi n F}= X(F)|_{F=\frac{k}{N}} \end{equation}si ottiene la definizione di DFT la cui rappresentazione grafica è quella in fig. 2 da cui si nota che :
- il periodo della DFT è compreso nell'intervallo \([0,1]\) e centrato in 1/2;
- non è periodica;
- in pratica la DFT è un campionamento nei punto \(k/N\) compreso nell'intervallo \([0;N-1]\)
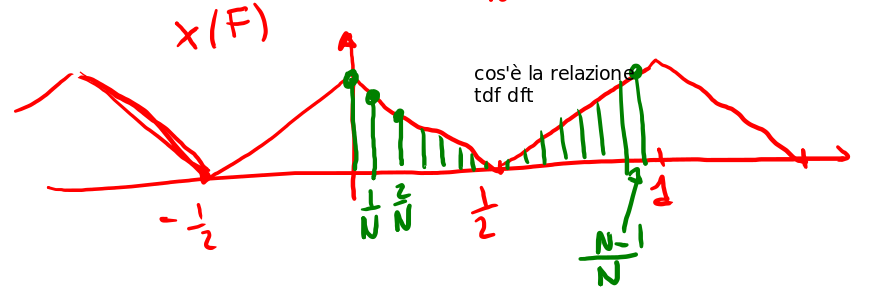
Figure 2: Relazione tra grafico della TDF e DFT
In modo analogo alla TDF si definisce la sua inversa IDFT tenendo conto del termine eliminato otteniamo :
\begin{equation}\label{eq:211} x[n]=\frac{1}{N}\sum_{n=0}^{N-1} X[k]e^{2\pi n F}= \frac{1}{N}\sum_{n=0}^{N-1} X[k]e^{2\pi n \frac{k}{N}} \end{equation}1.1. Relazione DFT - TDZ
1.1.1. Relazione TDZ -> DFT
come mostrato in fig 3 si nota la DFT altro non è che la TDF calcolata nei punti \(k/N\). In pratica campionando la TDZ ottengo la DFT
Figure 3: relazione TDZ DFT
1.1.2. Relazione DFT -> TDZ
1.2. Relazione TDF - DFT
1.2.1. Relazione TDF -> DFT
Deriva direttamente dalla \eqref{eq:210}
\begin{equation}\label{eq:303} X[k]=X(F)|_{F=k/N} \end{equation}1.2.2. Relazione DFT -> TDF
in cui \(\phi\) è una funzione detta interpolante e altro non è che la tDF di una \(rect\)
\begin{equation}\label{eq:305} \phi(F)=e^{-j2\pi F \frac{N-1}{2}} \frac{1}{N} \frac{sin(\pi Fn)}{sin(\pi F)} \end{equation}In considerazione della \eqref{eq:210} posso scrivere la seguente catena di relazioni :
\begin{equation}\label{eq:306} X(F)\ \overrightarrow{campiono}\ X[k]\ \overrightarrow{interpolazione}\ X(F) \end{equation}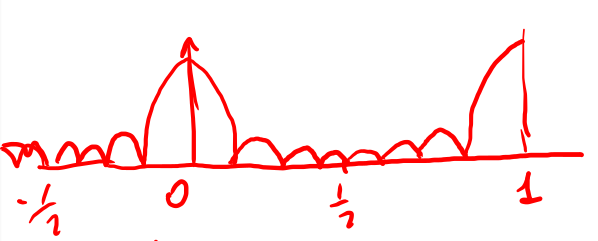
Figure 4: grafico di \(\phi(F)\)
1.3. Utilizzo della relazione TDF -> DFT per plottare grafici
vds esempio
1.4. Proprietà della DFT
1.4.1. Linearità : dalla definizione
1.4.2. Traslazione circolare
Si definisce traslazione circolare di una sequenza finita di periodo N la rotazione dell'(N-1)-esimo campione con quello in 0.
\begin{equation}\label{eq:400} x[n] \rightarrow X[k] \\ x[n-n_0] \rightarrow ? \end{equation} \begin{equation}\label{eq:401} DFT\{x[n-n_0]\}=\sum_{n=0}^{N-1}x[n-n_0]e^{-j2\pi \frac{k}{N} n}= \sum_{p=-n_0}^{N-1-n_0}x[p]e^{-j2\pi \frac{k}{N} (p+n_0)}= \\ e^{-j2\pi \frac{k}{N} n_0}\sum_{p=-n_0}^{N-1-n_0}x[p]e^{-j2\pi kp}= e^{-j2\pi \frac{k}{N} n_0}X_N[p] \end{equation}in merito da notare che :
- per \(p=-n_0\) si ha che \(X_N[-n_0]=x[-n_0]e^{-j2\pi k(-n_0)}\) ;
- per \(p=N-n_0\) si ha che \(X_N[-n_0]=x[N-n_0]e^{-j2\pi k(N-n_0)}\)
ma ricordando che \(X_N[p]\) è periodica di periodo N dunque \(X[-n_0]=X[N-n_0]\). Dunque se io effettuo uno shift a sx di uno la DFT non cambia e se ripeto l'operazione \(n_0\) volte la \eqref{eq:401} ottengo:
\begin{equation}\label{eq:402} DFT\{x[n-n_0]\}=e^{-j2\pi \frac{k}{N}n_0} \sum_{p=0}^{N-1}x[p]e^{-j2\pi \frac{k}{N}}=e^{-j2\pi \frac{k}{N} n_0}X[p] \end{equation}1.4.3. Traslazione in frequenza
\(X[k-k_0]\) \(\rightarrow\) \(x[n]e^{j2\pi \frac{k_0}{N} n}\)
1.4.4. Inversione temporale
In fig 5 è mostrato un esempio di inversione temporale in cui l'inversione avviene attorno al campione in 0.
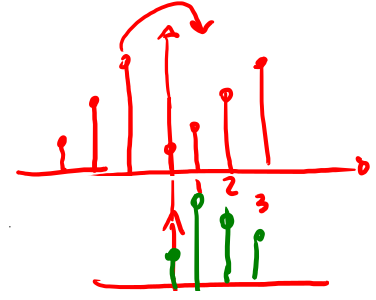
Figure 5: Esempio di inversione temporale
Da notare che il passaggio da \(x[-n]\) a \(x[N+ (-n)]\) è possibile per la periodicità N della sequenza dopodiché effettuo una traslazione di -1 ed ottengo la definizione di DFT. Nella \eqref{eq:500} non è introdotto il termine esponenziale a moltiplicare la DFT quando si effettuano traslazioni perché unitario dovuto alla traslazione di -1.
1.4.5. Simmetria
- se s\(x[n]\) è sequenza reale allora \(DFT_N\{x[-n]\}=X^*[k]\);
- \(DFT_N\{x^*[n]\}=X^*[-k]=X*[N+(-k)]\);
- sia \(x[n]\) un sequenza complessa allora :
- \(DFT\{Re(x[n])\}=DFT\{\frac{1}{2}(x[n]+ x^*[n])\}=\frac{1}{2}(X[k]+X^*[-k])=X_{pari}[k]\)
- infatti \(DFT\{Re(x^*[n])\}=DFT\{\frac{1}{2}(x^*[n]+ x[n])\}=\frac{1}{2}(X^*[-k]+X[k])=X^*_{pari}[k]\)
- \(DFT\{Im(x[n])\}=DFT\{\frac{1}{2}(x[n] - x^*[n])\} = j\frac{1}{2}(X[k]-X^*[-k])=X_{dispari}[k]\)
- infatti \(DFT\{Im(x^*[n])\}=DFT\{\frac{1}{2}(x^*[-n]- x[n])\}=-j\frac{1}{2}(X^*[-k]-X[k])=-DFT{Im(x[n])}\)
- \(DFT\{Re(x[n])\}=DFT\{\frac{1}{2}(x[n]+ x^*[n])\}=\frac{1}{2}(X[k]+X^*[-k])=X_{pari}[k]\)
- sia \(y[n]=x_1[n]+jx_2[n]\) con \(x_1[n]\) e \(x_2[n]\) reali e finite di durata N allora
- 5\(X_1[k]=DFT\{Re(y[n])\}=\frac{1}{2}(Y[k]+Y^*[-k])\);
- \(X_2[k]=DFT\{Im(y[n])\}=-j\frac{1}{2}(Y[k]-Y^*[-k])\);
Data una sequenza reale abbiamo che \(x[n]=x^*[n]\) e che la sua DFT ha la seguente proprietà \(X[k]=X[N-k]\) e dunque \(|X[k]|=|X[N-k]|\) . Quest'ultima proprietà può essere rappresentata nei grafici di fig 6, 7, 8. Da notare che tutte le simmetrie sono rispetto all'asse \(N/2\) e questo vale anche per la fase \(\angle X[k]=-\angle X[N-k]\).
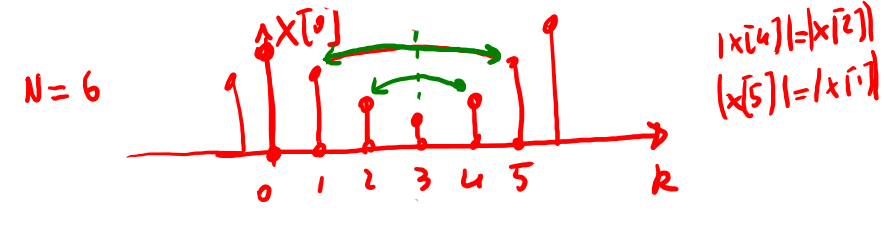
Figure 6: Esempio di simmetria pari rispetto all'elemento N/2=3
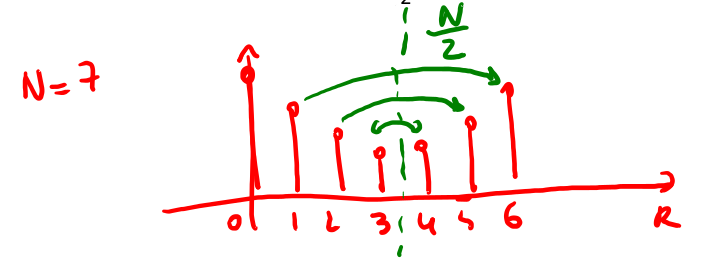
Figure 7: Esempio di simmetria dispari rispetto all'asse compreso tra l'elemento 3 e 4
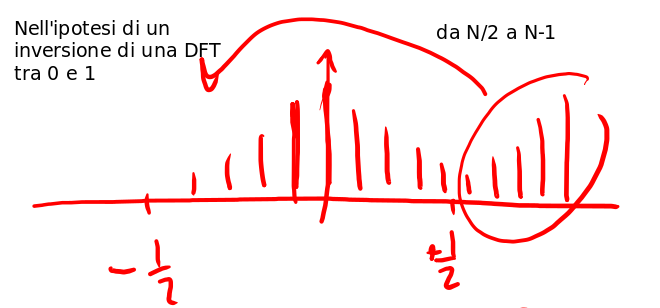
Figure 8: Esempio di simmetria della DFT
1.5. Teorema di Parsefal per la DFT
dimostrazione
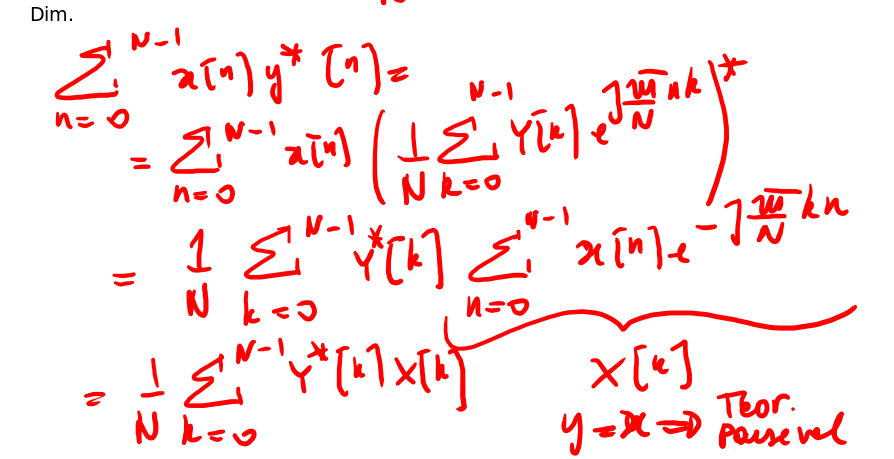
Figure 9: Dimostrazione del teorema di Parsefal per la DFT
2. Covoluzione Aperiodica ( lineare )
Spiegazione per via grafica
Siano \(x_1[n]\) e \(x_2[n]\) due sequenze aperiodiche come in fig. 10, rispettivamente di lunghezza M ed N, allora la covoluzione delle sequenze è quella della fig 11 dovuta all'evoluzione indicata nella fig 12.
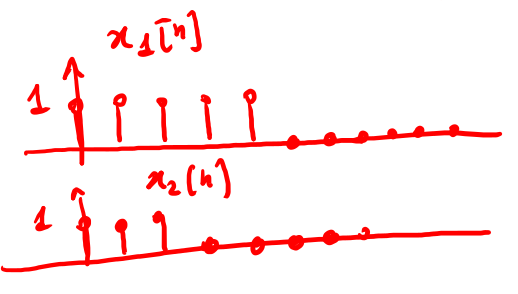
Figure 10: Esempio di due sequenze aperiodiche perché limitate
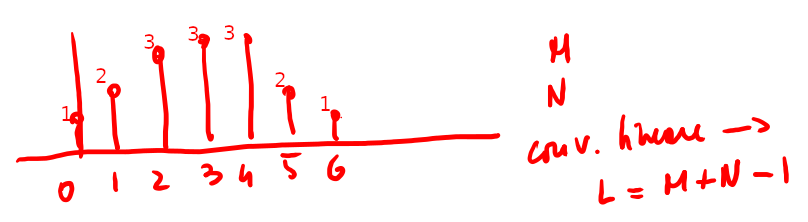
Figure 11: Covoluzione di due sequenze di lunghezza M ed N
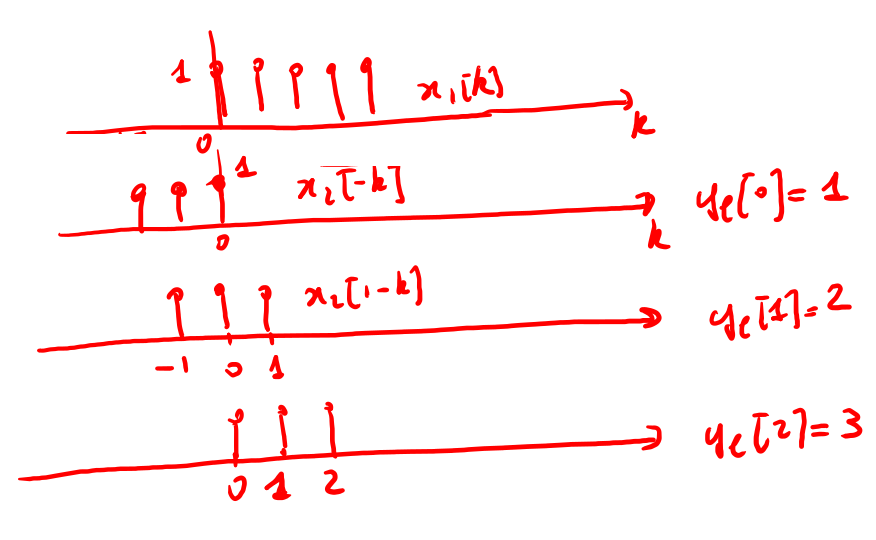
Figure 12: Evoluzione della covoluzione
3. Covoluzione circolare
Si applica a sequenze periodiche o periodizzate. Può anche essere utilizzata per effettuare filtraggi e implementata con un algoritmo veloce.
Quello che mi aspetto è che date due sequenze \(x_1[n], x_2[n]\) la loro covoluzione nel dominio del tempo si trasformi in un prodotto nel dominio della frequenza.
\begin{equation}\label{eq:601} DFT\{x_1[n] \oplus x_2[n]\}=X_1[k]X_2[k] \end{equation}Dimostrazione
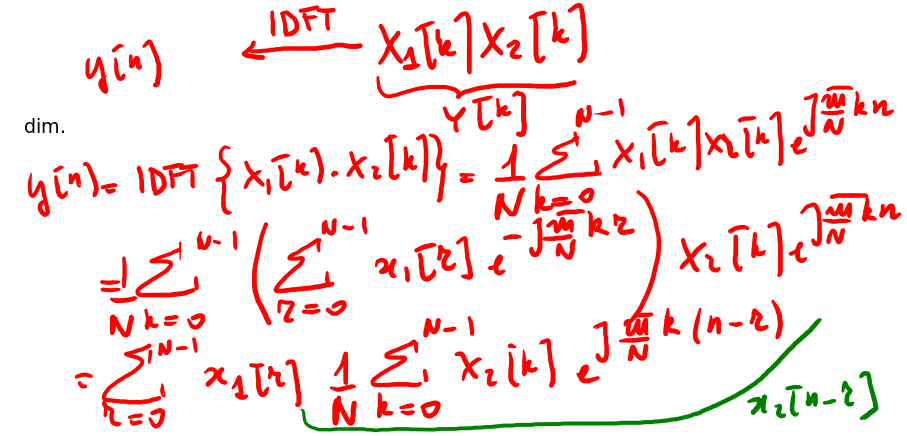
Figure 13: Dimostrazione della prop della covoluzione circolare
3.1. Covoluzione circolare di seq. non periodiche
Problema : come utilizzare la covoluzione circolare per calcolare una covoluzione lineare.
Il problema si pone perché la maggior parte delle sequenze sono lineari ( aperiodiche ).
In fig 19 è mostrata la covoluzione circolare di due sequenze aperiodiche \(x_1[n]\) e \(x_2[n]\) di lunghezza diversa ( 14 ) dopo che queste sono state periodizzate 15 con uno stesso periodo N. All'uscita dei blocchi DFT entrambi i segnali hanno periodicità N.
Nel seguito si descrive la covoluzione circolare ( fig 17 ) per funzioni periodizzate in N:
- Inversione temporale nell'intervallo \([0,N-1]\)
- l'elemento in 0 rimane fermo;
- l'elemento nell'n-esima posizione si sposta in \(N-n\)
- Traslazione temporale nell'intervallo \([0,N-1]\)
- rotazione verso sx di n posizioni, in questo caso n=1, in pratica l'elemento in 0 va in 1 quello in 5 in 0. Come si nota l'elemento estremo dx della finestra N esce e rientra dall'estremo opposto;
Dal grafico di fig 19 si ricava che :
- la lunghezza della covoluzione circolare e minore di quella lineare;
- alcuni campioni di \(y_c[n]\) coincidono con \(y_l[n;]\);
- un campione che non coincide è quello in 0 in quanto la covoluzione per l'indice n=0 \(y[0]\) vi è la presenza contemporanea degli elementi in 4 ( vds fig 17 );
Al fine di eliminare il problema della sovrapposizione degli elementi devo utilizzare un passo di campionamento maggiore, ad esempio N=7 vds fig 20. In pratica se \(M_1\) ed \(M_2\) sono le lunghezze di due sequenze allora per ottenere la coincidenza tra \(y_l\) e \(y_c\) devo utilizzare con un periodo di lunghezza \(M_1+M_2 -1\). Nel caso in cui \(M_1\) sia la lunghezza maggiore delle due sequenze se si usasse una periodizzazione uguale alla maggiore della due lunghezze avrei :
- i primi \(M_2 -1\) campioni di \(y_c[n]\) non coincidono con quelli \(y_l[n]\);
- i successivi \(M_1 - M_2 +1\) campioni di \(y_c[n]\) coincidono \(y_l[n]\);
Altro metodo per ottenere una sequenza aperiodica è quello mostrato in fig 21 in cui utilizzo come lunghezza della convoluzione circolare la maggiore delle due periodizzazioni di modo che quello che mi rimane eliminando da questa tanti campioni quanto quelli della sequenza minore ( non coincidono con quelli della sequenza lineare ) sono i campioni che coincidono con \(y_l[k]\)
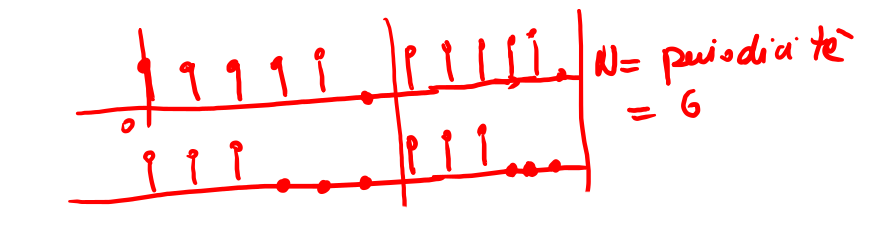
Figure 14: Sequenze periodizzate
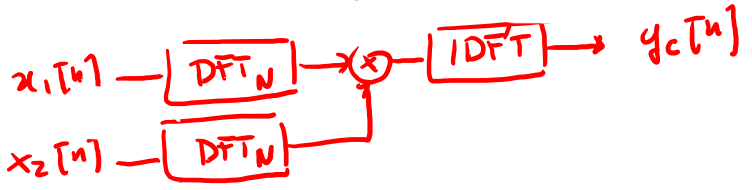
Figure 15: Come periodizzare due sequenze.
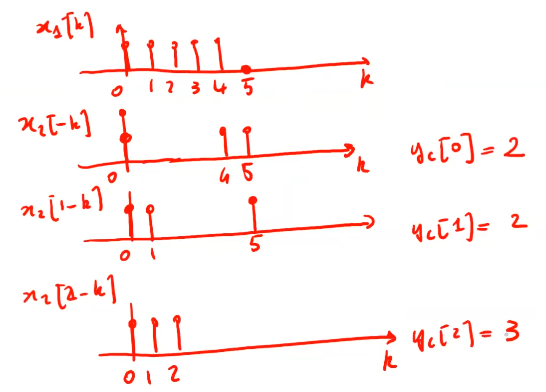
Figure 16: Esempio di covoluzione circolare

Figure 17: Esempio di covoluzione circolare
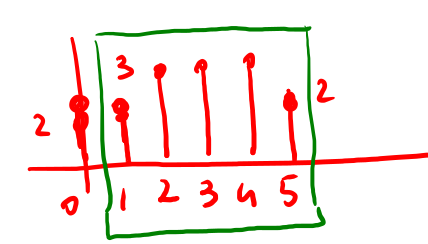
Figure 18: \(y_c[n]\) con periodizzazione con N=7
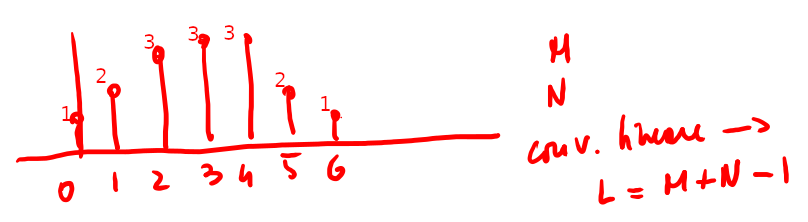
Figure 19: \(y_l[n]\) con periodizzazione con N=7
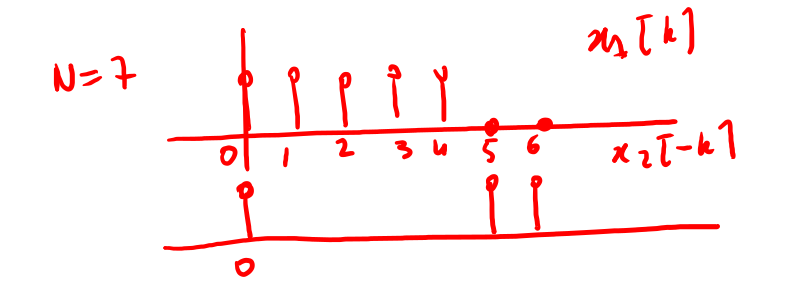
Figure 20: Esempio di periodizzazione con N=7
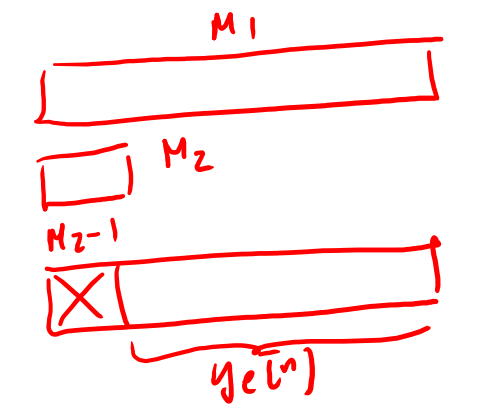
Figure 21: Altro modo di ottenere una sequenza aperiodica
3.2. Convoluzione veloce
Utilizzo della FFT per il calcolo della convoluzione in sistemi LTI di tipo FIR.
\begin{equation}\label{eq:7000} y[n]=h[n]*x[n-k]=\sum_{k=0}^{N-1}h[k]x[n-k] \end{equation}per il calcolo della complessità si considerano solo gli N prodotti complessi oppure \(4N\) moltiplicazioni reali. Sia che si utilizzi il metodo OVERLAP-AND-ADD oppure OVERLAP-AND-SAVE lo schema implementativo è quello di fig 22 il cui costo è \((L/2)\log_2 L + L + (L/2)\log_2 L\) così composto :
- \((L/2)\log_2 L\) costo dei blocchi DFT di x[n] e IDFT;
- \(L\) costo delle moltiplicazioni;
Inoltre il segnale in ingresso deve essere suddiviso in blocchi t.c. sia possibile elaborarlo in modo finito come in fig 23.
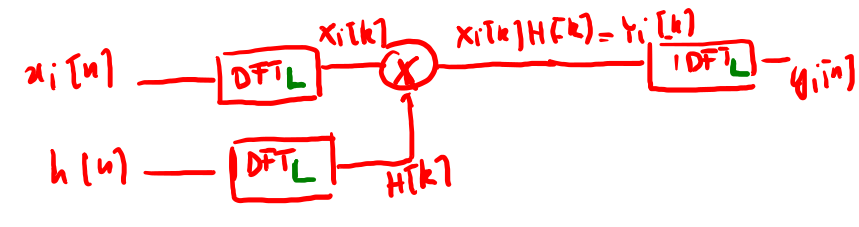
Figure 22: Circuito per covoluzione circolare
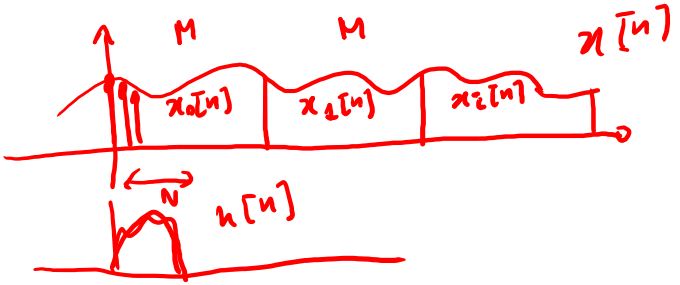
Figure 23: Esempio di suddivisione del segnale
3.2.1. OVERLAP-AND-ADD
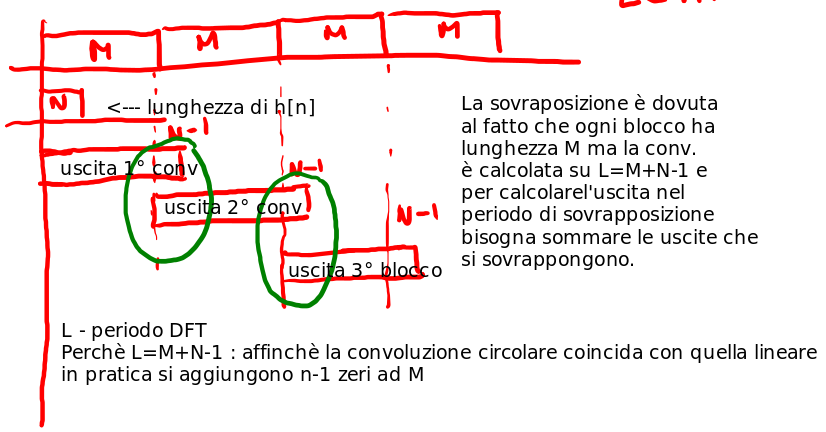
Figure 24: Esempio si suddivisione in overlap-and-add
3.2.2. OVERLAP-AND- SAVE
I campioni scartati sono stati calcolati nel ciclo precedente.
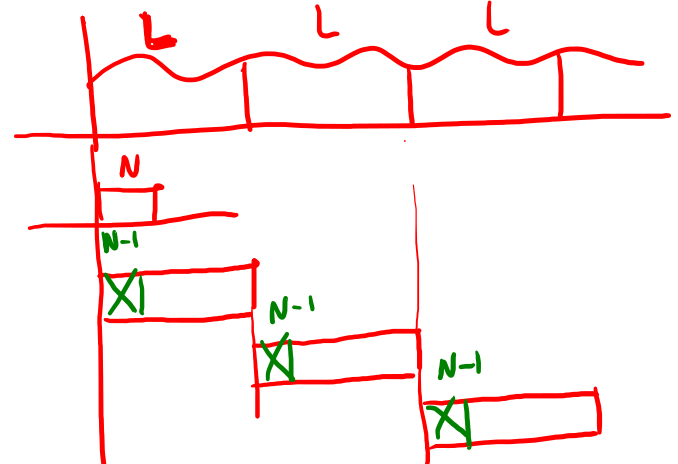
Figure 25: Esempio di overlap-and-save
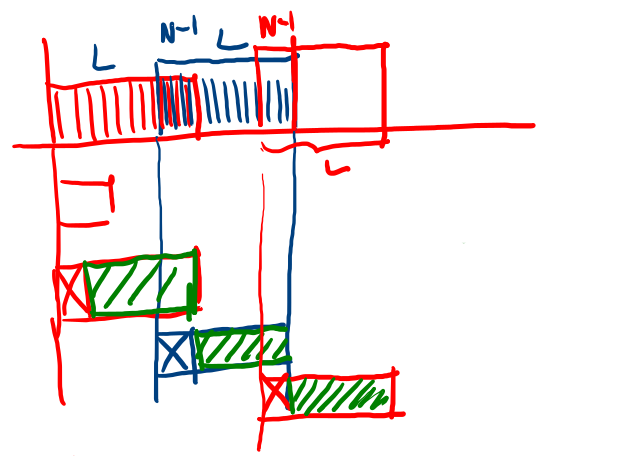
Figure 26: Esempio di sovrapposizione della finestra
4. FFT - Fast Fourier Trasform - Implementazione DFT
Indica la procedura per implementare la DFT. Basata su tecniche di decimale di tempo o di frequenza. Le tecniche di implementazione si basano sulla lunghezza della sequenza da trasformare :
- sequenza lunga \(N=r^p\) metodo della radice \(r\)
- decimazione in \(r\) sotto-sequenze ;
- calcolo della DFT in \(N/r\) campioni. Ciò significa che nel calcolo della DFT compaiono contemporaneamente r sommatorie una per ogni campione di passo \(N/r\);
- combina le \(r\) -esima sotto-sequenza con circuiti di tipo butterfly;
- itera il procedimento al punto 2;
- sequenza \(N \neq r\) ma scomponibile in \(M\) fattori primi
- scompongo la sequenza in parti t.c. ognuna di esse sia esprimibile con il modo delle radici di cui al punto 1: \(N=\prod_{i=1}^{M}r_i^{p_i}=\prod_{i=1}^{M}N_i\)
- lunghezza della sequenza in numeri primi
- vds in seguito.
Complessità : conteggio delle moltiplicazioni complesse ognuna delle quali scomponibile in quattro addizioni e quattro moltiplicazioni reali.
\((a+jb)(c+jd)=ac + jad + jbc - db\)
ma per semplicità si considerano solo le moltiplicazioni in quanto più costose.
L'implementazione fisica avviene mediante l'utilizzo di circuiti tipo butterfly ( fig 31 ) in cui per ogni istante temporale si hanno tanti ingressi quante sono le sotto-sequenze \(r\) e la cui complessità è data da \(\frac{r-1}{r}N\log_rN\) moltiplicazioni complesse.
4.1. Metodo delle radici - Decimazione nel tempo
L'utilizzo del metodo delle radici prevede la suddivisione della sequenza in \(N/p\) parti con \(p\) indice della radice.
Caso con \(N=2^2\). Ciò significa suddividere la sequenza in due parti e prendere i campioni pari e dispari separatamente :
Sia \(W_N=e^{-j2\pi \frac{k}{N} n}\) \(\rightarrow\) \(W_N^2=e^{-j4\pi \frac{k}{N} n}=e^{-j2\pi \frac{k}{N/2} n}=W_{\frac{N}{2}}\)
\begin{equation}\label{eq:1000} X[k]=\sum_{n=0}^{N-1}x[n]e^{-j2\pi \frac{k}{N} n}= \sum_{n=0}^{N-1}x[n]W_N^{kn}=\\ \sum_{n\ pari}x[n]W_N^{kn} + \sum_{n\ dispari}x[n]W_N^{kn}=\\ \sum_{r=0}^{\frac{N}{2}-1}x[2r]W_N^{k2r} + \sum_{r=0}^{\frac{N}{2}-1}x[2r+1]W_N^{k(2r+1)}=\\ \sum_{r=0}^{\frac{N}{2}-1}x[2r](W_N^2)^{kr} + \sum_{r=0}^{\frac{N}{2}-1}x[2r+1](W_N^2)^{kr}W_N^k=\\ \sum_{r=0}^{\frac{N}{2}-1}x[2r]W_{\frac{N}{2}}^{kr} + W_N^k\sum_{r=0}^{\frac{N}{2}-1}x[2r+1]W_{\frac{N}{2}}^{kr}=\\ A[k] +W_N^kB[k] \end{equation}in cui \(A[k]\) e \(B[k]\) sono due DFT a N/2. L'implementazione fisica avviene considerando che per ogni istante temporale punti implementabili con una butterfly elementare ( 2 ingressi - 2 uscite ) come quella in fig 31. Inoltre
\begin{equation}\label{eq:1001} x[k]=A[k]+W_N^kB[k] \\ X[k+ N/2]=A[k] +W_N^{(k +N/2)}B[k]= ... =A[k] -W_N^kB[k] \end{equation}Caso con \(N=4^2\). Ciò significa suddividere la sequenza in quattro parti e prendere i campioni pari e dispari separatamente :
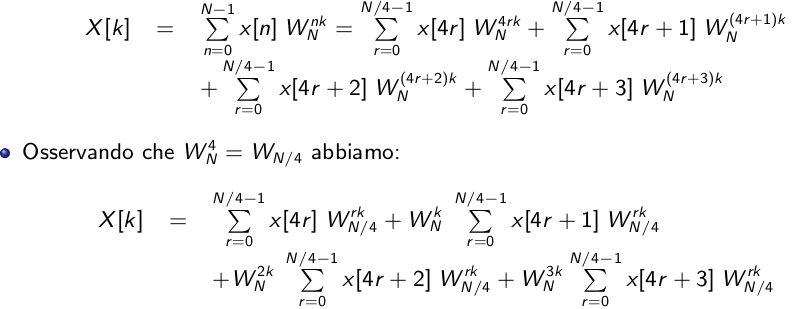
Figure 27: Esempio di FFT di radice 4

Figure 28: Calcolo congiunto di una DFT di indice 4
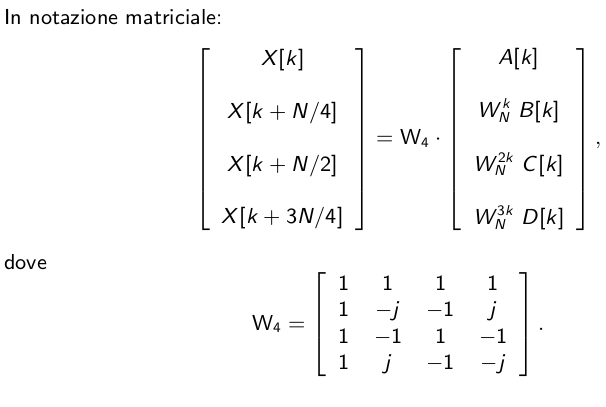
Figure 29: Notazione matriciale di una DFT di radice 4
4.2. IFFT - Inversione della FFT
La definizione di \(IFFT\)
\begin{equation}\label{eq:3000} x[n]=IFFT\{X[k]\}=\frac{1}{N}\sum_{k=0}^{N-1}X[k]e^{j2\pi \frac{k}{N} n}= \frac{1}{N}\sum_{k=0}^{N-1}X[k]W_N^{-kn} \end{equation}la differenza con la FFT è il fattore moltiplicativo \(1/N\) e l'esponenziale negativo.
4.2.1. 1° metodo alternativo
Applicazione della FFT ad una FFT
\begin{equation}\label{eq:3001} FFT\{X[n]\}=\sum_{n=0}^{N-1}X[n]e^{-j2\pi \frac{k}{N} n}= \sum_{n=0}^{N-1} \left (\sum_{r=0}^{N-1} x[r]e^{-j2\pi \frac{r}{N} n} \right )e^{-j2\pi \frac{k}{N} n}= \\ \sum_{r=0}^{N-1} x[r] \left (\sum_{n=0}^{N-1} e^{-j2\pi \frac{r}{N} n} e^{-j2\pi \frac{k}{N} n} \right )= \sum_{r=0}^{N-1} x[r] \left (\sum_{n=0}^{N-1} e^{-j\frac{2\pi}{N} (k + r)n} \right )= \\ x[-k]N \end{equation}4.2.2. 2° metodo alternativo
Applicazione della FFT alla coniugata della FFT
\begin{equation}\label{eq:3002} FFT\{X^*[n]\}= \sum_{n=0}^{N-1}X^*[n]e^{-j2\pi \frac{k}{N} n}= \sum_{n=0}^{N-1} \left (\sum_{r=0}^{N-1} x^*[r]e^{j2\pi \frac{r}{N} n} \right )e^{-j2\pi \frac{k}{N} n}= \\ \sum_{r=0}^{N-1} x^*[r] \left (\sum_{n=0}^{N-1} e^{-j2\pi \frac{r}{N} n} e^{-j2\pi \frac{k}{N} n} \right )= \sum_{r=0}^{N-1} x^*[r] \left (\sum_{n=0}^{N-1} e^{-j\frac{2\pi}{N} (k - r)n} \right )= \\ x^*[k]N \end{equation}4.2.3. 3* metodo alternativo
Scambio della parte reale e immaginaria
\begin{equation}\label{eq:3003} Nx[n]=FFT\{X*[n]\}*=FFT\{j(-j)X^*[n]\}^*=jFFT\{jX^*[n]\}^* \end{equation}che implementato diventa lo schema di fig 30.

Figure 30: Implementazione della FFT con scambio della parte reale e immaginaria
4.3. Implementazione mediante Butterfly
La \eqref{eq:1001} può essere implementata come in fig 31 che applicata in modo ricorsivo ad una sequenza lunga 8 permette di ottenere la fig 32. Come si nota andando a ritroso da destra ogni sezione precedente è ottenuta applicando la \eqref{eq:1000} alla sequenza degli ingressi della sezione successiva fino a quando non si giunge all'implementazione butterfly il cui numero d'ingressi coincide con la radice. In fig 33 è mostrato l'applicazione del metodo della radice con indice 4 ( sequenza lunga 16 )
Per il calcolo della complessità, ad esempio per una radice di indice 2, è necessario moltiplicare la complessità di ogni singolo stadio \(N/2\) per il numero totale di stadi \(\log_2 N\) per cui nel caso di specie vale \(3=\log_2 8\). Più in generale \(O(\frac{N}{2}\log_2N)\).
Per quello invece con radice di indice \(r=4\) abbiamo che per ogni stadio la complessità è \(\frac{r-1}{r}N=\frac{3}{4}N\) di ogni sezione per un totale di \((3/4)N\log_4 N\) sezioni.
Come risultato della ripetuta applicazione della decimazione nel tempo ad ogni stadio, l’ordinamento dei campioni in ingresso al sistema che esegue l’algoritmo FFT non è quello naturale. L’ordinamento risultante viene detto a bit invertiti (bit reverse order); il motivo di tale denominazione deriva dal fatto che l’indice dei campioni e la posizione occupata all’ingresso dell’algoritmo FFT hanno espressioni (in binario) invertite l’una rispetto all’altra ( vds fig 34 )
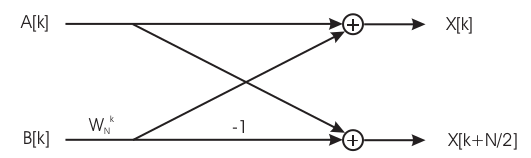
Figure 31: Implementazione tipo butterfly
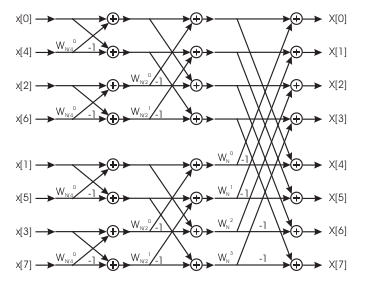
Figure 32: Applicazione dell'implementazione
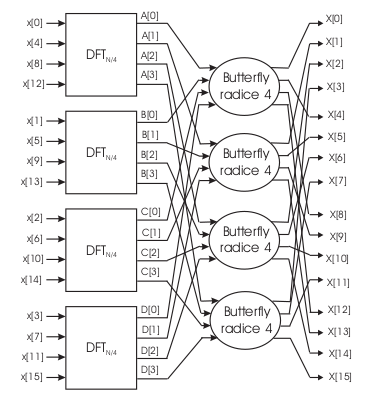
Figure 33: FFT con radice di indice 4
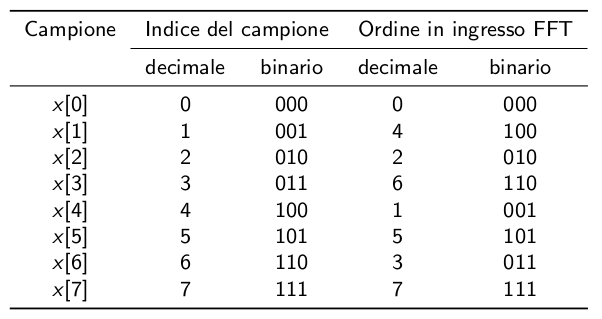
Figure 34: Ordine ingresso/uscita di una FFT
4.4. Metodo delle radici - Decimazione in frequenza
Analogo a quello a decimazione nel tempo ma applicato al dominio in frequenza. Per una sequenza N potenza del due si considerino separatamente i campioni pari ( \eqref{eq:4000} ) e quelli dispari ( \eqref{eq:4001} ) si ha che :
\begin{equation}\label{eq:4000} X[2r]=\sum_{n=0}^{N-1}x[n]W_N^{2nr}= \sum_{n=0}^{N/2-1}x[n]W_N^{2nr} + \sum_{n=N/2}^{N-1}x[n]W_N^{2nr}=\\ \sum_{n=0}^{N/2-1}x[n]W_N^{2nr} + \sum_{n=N/2}^{N-1}x[n + \frac{N}{2}]W_N^{2(n +N/2)r}=\\ \sum_{n=0}^{N/2-1}x[n]W_{N/2}^{nr} + \sum_{n=N/2}^{N-1}x[n + \frac{N}{2}]W_{N2}^{(n+N/2)r}=\\ \sum_{n=0}^{N/2-1} \left ( x[n] + x[n + \frac{N}{2}] \right ) W_{N2}^{nr}=\\ \end{equation}in cui \(W_{N/2}^{r N/2}=1\) per ogni \(r\) intero.
\begin{equation}\label{eq:4001} X[2r+1]=\sum_{n=0}^{N-1}x[n]W_N^{n(2r+1)}= \sum_{n=0}^{N/2-1}x[n]W_N^{n(2r+1)} + \sum_{n=N/2}^{N-1}x[n]W_N^{n(2r+1)}=\\ \sum_{n=0}^{N/2-1}x[n]W_N^{2nr} + \sum_{n=N/2}^{N-1}x[n + \frac{N}{2}]W_N^{(n +N/2)(2r+1)}=\\ \sum_{n=0}^{N/2-1}x[n]W_N^{2nr} + \sum_{n=N/2}^{N-1}x[n + \frac{N}{2}]W_N^{(N/2)(2r+1)}W_N^{n(2r+1)}=\\ \sum_{n=0}^{N/2-1} \left [ \left ( x[n] - x[n + \frac{N}{2}] \right ) W_N^n \right ]W_{N/2}^{nr} \end{equation}dove \(W_N^{(2r+1)N/2}=e^{j\frac{2\pi}{N}(2r+1)N/2}=e^{j\pi(2r+1)}=-1\)
- I campioni \(X[2r ]\) sono la DFT a N/2 campioni della sequenza \(a[n] = (x[n] + x[n + N/2])\) con \(n = 0, 1, . . . , N/2 − 1\)
I campioni \(X[2r + 1]\) sono la DFT a N/2 campioni della sequenza \(b[n] = (x[n] - x[n + N/2])W_N^n\) con \(n = 0, 1, . . . , N/2 − 1\).
che implementata con struttura butterfly diventa quella indicata in fig 35 che differisce da quella a decimazione del tempo ( fig 31 ) per la posizione della moltiplicazione complessa anche se il costo rimane lo stesso. Inoltre confrontando la fig 36 con la fig 32 si nota che le strutture sono invertite
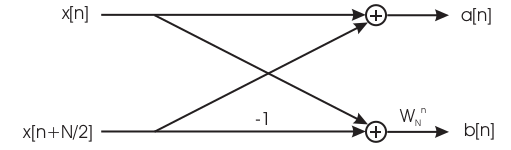
Figure 35: Struttura Butterfly per decimazione in frequenza
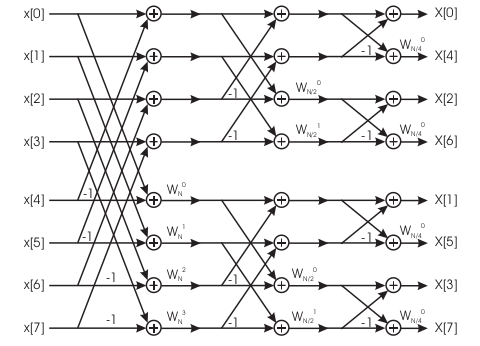
Figure 36: Struttura butterfly per una sequenza N=8 - costo \((N/2)\log_2 N\)