Trasformata di Fourier

1. Funzione Rect
2. Passaggio al limite della SDF
3. Convergenza
4. Proprietà
5. Prontuario

1. Funzione Rect

Nell'immagine di seguito e' riportato il grafico una generica rect

Figure 1: grafico della rect

2. Passaggio al limite della SDF

Nell'ipotesi che un qualsiasi segnale aperiodico possa essere rappresentato da una base \(X_{T_0}(t)=x(t)rect(\frac{t-T_0}{T})\) che se portata al limite \(\lim_{T_0 -> \infty}X_{T_0}(t)=x(t)\) rende indistinguibile la troncata con il segnale allora si può scrivere (vds 2 ) inoltre se utilizziamo la notazione per rappresentare il treno d' impulti \(X_{T_0}(t - k T_0)=x(t)rect(\frac{t- k T_0}{T})\) possiamo scrivere :

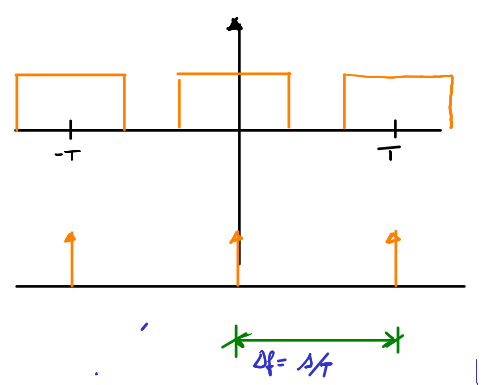
Figure 2: grafico del treno d'impulsi

\begin{equation}\begin{split} \label{orgf07871b} x(t)=\sum_{k=-\infty}^{\infty} X_{T_0} (t-kT_0)= \\ \sum_{k=-\infty}^{\infty} x(t)rect(\frac{1-kT_0}{T})= \\ \sum_{k=-\infty}^{\infty}G(k)e^{j2\pi \frac{k}{T_0}t} \end{split}\end{equation}

in cui :

\begin{equation} \label{eq:2} G(k) = \frac{1}{T_{0}} \int_{-\infty}^{\infty} X_{T_0}(t)e^{-j2\pi \frac{k}{T_{0}} t} d_{t} =\\ \frac{1}{T_{0}} \int_{-\infty}^{\infty} x(t) rect(\frac{t}{T_{0}}) e^{-j2\pi \frac{k}{T_{0}} t} d_{t} =\\ \frac{1}{T_{0}} \int_{T_{0}/2}^{T_{0}/2} x(t)e^{-j2\pi \frac{k}{T_{0}} t} d_{t} = f_0 G(kf_0) \end{equation}

e dunque la SDF, riscritta in funzione di \(f_0\) diventa :

\begin{equation} \label{orgf13dc6a} x(t)=f_0\sum_{k=-\infty}^{\infty}G(kf_0)e^{j2\pi kf_0 t} \end{equation}

Applicando l'operazione di limite alla troncata base estendo la finestra ( \(T_0 \rightarrow \infty\) ) all'intero segnale per cui :

\(f_0\) diventa \(d_f\)
\(kf_0=kd_f=f\)
\(\sum\) diventa \(\int\) inteso come somma di Rieman.

per cui la \eqref{eq:2} e la \eqref{eq:3} diventano :

\begin{equation} \label{eq:03} G(f) = \int_{-\infty}^{\infty} x(t)e^{-j2\pi {k}{ft}} d_{t} \end{equation} \begin{equation} \label{eq:4} x(t) = d_f\int_{-\infty}^{\infty}G(f)e^{j2\pi f t} d_f = \int_{-\infty}^{\infty}G(f)e^{j2\pi f t}d_f \end{equation}

in cui la \eqref{eq:03} e la \eqref{eq:4} altro non sono, rispettivamente, che la definizione di TDF e della sua inversa.

Da notare che tutte le trasformate sono funzioni
aperiodiche che a differenza di quelle discrete che sono
perioriche.

3. Convergenza

4. Proprietà

4.1. linearità

deriva dall'utilizzo dell'integrale nella definizione;

4.2. dualita

\(x(t) \rightarrow X(f) \rightarrow x(-t)\)

4.3. variazione di scala

\(h(t)=x(at) \rightarrow H(f)=\frac{1}{|a|}X(\frac{f}{a})\) la variazione di scala influenza il modulo e non la fase di un segnale;

4.4. traslazione temporale

\(h(t)=x(t \pm t_0) \rightarrow H(f)=e^{\pm j 2\pi f_0}X(f)\)

4.5. modulazione

\(h(t)=x(t)e^{\pm j 2\pi f_0 t} \rightarrow H(f)=X(f \mp f_0)\) La modulazione influisce sullo spettro della fase.

4.6. prodotto/covoluzione

\(h(f)*x(f) \rightarrow H(f)X(f)\)
\(h(f)x(f) \rightarrow H(f)*X(f)\)

4.7. coniugo

Un segnale reale o complesso ammette TDF formata da parte reale e immaginaria che però sotto oppurtune condizioni diventano mutuamente esclusive. In generale un segnale \(x(t)\) ammette TDF del tipo \(X(f)=Re\{X(f)\} + jIm\{X(f)\}=|X(f)|\cos (\theta) + j|X(f)|\sin (\theta)\) dove la parte reale è sempre simmetrica mentre quella immaginaria è sempre antisimmetrica.

\begin{equation}\begin{split} x(t)=\int^{\infty}_{-\infty}X(f)e^{j2\pi ft}df= \int_{-\infty}^{0}X(f)e^{j2\pi ft}df + X(0) + \int^{0}_{\infty}X(f)e^{j2\pi ft}df=\\ =X(0) - \int^{-\infty}_{0}X(f)e^{j2\pi ft}df + \int^{0}_{\infty}X(f)e^{j2\pi ft}df =\\ =X(0) + \int^{0}_{\infty}X(-f)e^{-j2\pi ft}df + \int^{0}_{\infty}X(f)e^{j2\pi ft}df =\\ \end{split}\end{equation}

Una dimostrazione delle proprietà sopra elencate la si ha osservando come un segnale \(x(t)\) reale può essere rappresentato in forma trigonometrica utilizzanzo la sua TDF:

per cui

\begin{equation}\begin{split} con\ X(f)\ pari\ \Rightarrow x(t)=X(0) + 2 \int^{0}_{\infty}G(f) \frac{[e^{j2\pi ft} + e^{-j2\pi ft}]}{2}df= X(0) + 2 \int^{0}_{\infty}X(f)cos(2\pi ft)df \\ con\ X(f)\ dispari\ \Rightarrow x(t)=X(0) + 2 \int^{0}_{\infty}X(f) \frac{[e^{j2\pi ft} - e^{-j2\pi ft}]}{2}df= X(0) + 2j \int^{0}_{\infty}X(f)sin(2\pi ft)df \end{split}\end{equation}

Nella fig. 3 un riepilogo dell'ultima parte della teoria. \(x^c(t) \rightarrow X^c(-f)\)

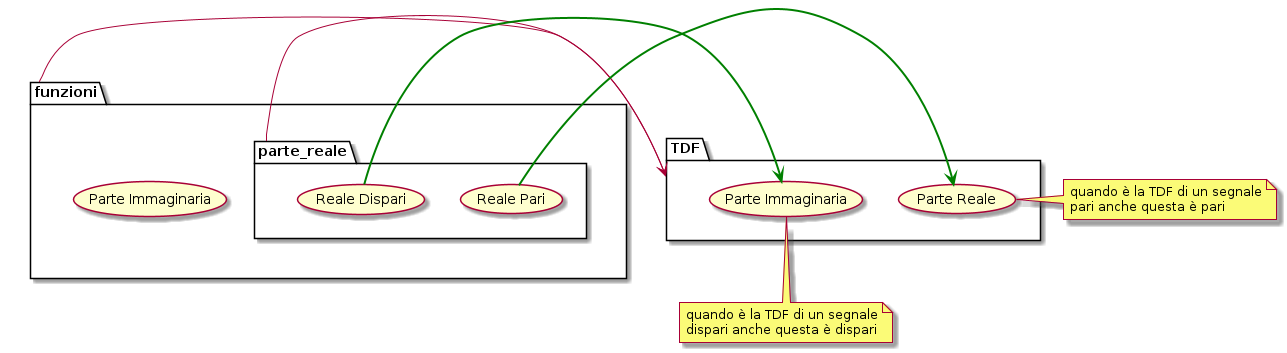
Figure 3: riepilogo della prop. del coniugo

4.8. Teorema di Derivazione

\(\frac{d^n}{d_t}x(t)\ \Rightarrow X'(f)=(j2\pi f)^n X(f)\)

In pratica sia \(x(t)\) un segnale reale e \(x^1(t)\) la sua derivata prima e \(x^2(t)\) la sua derivata seconda allora se non riesco a calcolare la TDF di \(x(t)\) posso derivare fino a quando non ottengo una funzione, nel nostro caso \(x^2(t)\), di cui so calcolare la derivata allora :

\begin{equation} x(t) \Rightarrow x^1(t) \end{equation}

Nella fig. 4 un esempio applicativo del teorema

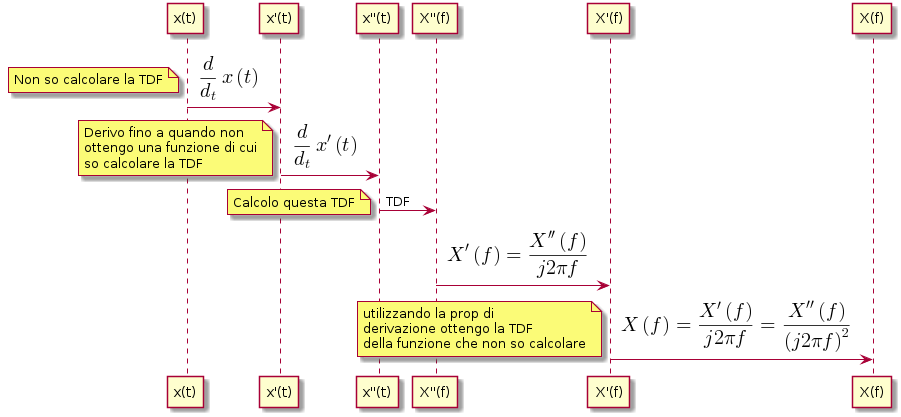
Figure 4: riepilogo della prop. della derivata

4.9. Teorema d'Integrazione

PREMESSA : vds teoria della delta di Dirac

Sia \(x(t)=\int_{-\infty}^{t}g(\alpha)d_\alpha\) come mostra il grafico seguente per cui

\begin{equation}\begin{split} x(t)=\int_{-\infty}^{t}g(\alpha)d_\alpha= \\ = \int_{-\infty}^{\infty}g(\alpha)u(t - \alpha)d_\alpha=g(t)*u(t) \end{split}\end{equation}

la cui TDF è

\begin{equation}\begin{split} X(f)=G(f)U(f)=G(f)[\frac{1}{j2\pi f} + \frac{\delta(f)}{2}]= \\ = \frac{G(f)}{j2\pi f} + G(f)\frac{\delta(f)}{2}= \\ = \frac{G(f)}{j2\pi f}+ \frac{G(0)}{2} \end{split}\end{equation}

per cui se nel dominio del tempo vale sempre la seguente relazione

\(x(t)=\int x'(t)d_t \Rightarrow X(f)=\frac{X^{'}(f)}{j2\pi f}+ \frac{X^{'}(0)}{2}\)

nel dominio della frequenza si ha che

\(X(f)=\frac{X'(f)}{j2\pi f}\) vale solo se \(X^{'}(0)=0\) cioè per segnali privi di componente continua ( segnali ad energia finita ).

4.10. Crossrelazione

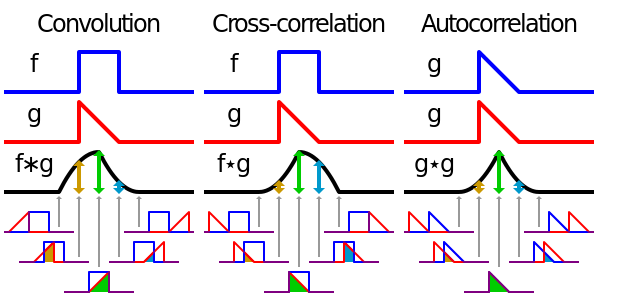
Figure 5: Sintesi

Relazione lineare tra due variabili che per i segnali ne misura la somiglianza. Si definisce come :

\begin{equation}\begin{split} C_{12}(\alpha)=(x_1(t) \star x_2(t))(\alpha)=(x_1(t) \otimes x_2(-t))(\alpha)=\int_{-\infty}^{\infty} x_1(t + \alpha)x_2^c(t)d_t= \\ = \int_{-\infty}^{\infty} x_1^c(t)x_2(t + \alpha)d_t\\ da \ cui\ \\ F[C_{12}(\alpha)]=X_1(f)X_2^c(-f)=S_{12}(f) \end{split}\end{equation}

in cui \(\alpha\) ( in blu ) rappresenta la finestra di covoluzione. La differenza con la convoluzione è il segno \(+\).

Nel caso in cui \(x(t)\) sia un segnale allora :

\(S_{12}(f)\) rappresenta lo spettro di energia mutua o densità spettrale di energia mutua;
dalla proprietà che afferma che \(x^c(t) \rightarrow X^c(-f)\) e \(x^c(-t) \rightarrow X^c(f)\) si ottiene \(S_{12}(f)=S^c_{21}(f)\) che ne caso di segnali reali si trasforma in \(S_{12}(f)=S_{21}(-f)\), inoltre per segnali reali di ha che \(S_{12}(f)S_{21}(f)=G_1(f)G_2^c(f)G_2(f)G_1^c(f)=|G_1(f)|^2|G_2(f)|^2\);

4.10.1. Riepilogo

	\(C_{12}(\alpha)\) \ \(\alpha\)	\(=0\)	\(\neq 0\)
1	0	perp.	incorrelati
2	\(\neq 0\)	paralleli/TEO di P.	grado di somiglianza

4.10.2. Caso con \(\alpha \neq 0\)

Nel caso \(C_{12}(\alpha) \neq 0\) misura del grado di somiglianza;
Nel caso \(C_{12}(\alpha)=0\) i segnali sono incorrelati.
TEO: CNS affinchè due segnali siano incorrelati è che
\(G_1(f)G^c_2(f)=0\)

4.10.3. Caso \(\alpha=0\)

Quando \(C_{12}(0)=0\) si parla di segnali ortogonali. Se invece \(C_{12}(0) \neq 0\) si dice che due segnali sono segnali parallelli.

Per la giustificazione di quanto sopra basta ricordare che :

\begin{equation}\begin{split} \lvert C_{12}(0) \lvert ^2 =\lvert \int_{-\infty}^{\infty} x_1(t)x_2^c(t)d_t \rvert ^2 = \\ = \int_{-\infty}^{\infty} |x_1(t)|^2 |x_2^c(t)|^2 d_t \end{split}\end{equation}

e che ogni \(\int_{-\infty}^{\infty} ... d_t\) può essere visto come un vettore complesso di componenti \(x=a +jb\).

Nel caso \(C_{12}(0)=0\)

\begin{equation}\begin{split} \lvert C_{12}(0) \lvert ^2 =\lvert \int_{-\infty}^{\infty} x_1(t)x_2^c(t)d_t \rvert ^2 = \\ \lvert (a_1 +jb_1) (a_2 +jb_2) \rvert ^2 = \lvert a_1a_2 +ja_1b_2 + ja_2b_1 - b_1b_2 \rvert ^2 = \\ \lvert (a_1a_2 - b_1b_2) + j(a_1b_2 + a_2b_1) \rvert ^2 =\\ (a_1a_2 - b_1b_2)^2 + (a_1b_2 + a_2b_1)^2 = 0 \\ da\ cui\ \\ [(a_1a_2 - b_1b_2), (a_1b_2 + a_2b_1)] = [0,0] \end{split}\end{equation}

l'unica combinazione possibile è che i due vettori siano perpendicolari.

Nel caso \(C_{12}(0) \neq 0\)

\begin{equation}\begin{split} \lvert C_{12}(0) \rvert ^2=\lvert \int_{-\infty}^{\infty} x_1(t)x_2^c(t)d_t \rvert ^2=\\ =\int_{-\infty}^{\infty} \lvert x_1(t) \rvert ^2 d_t \int_{-\infty}^{\infty} \lvert x_2^c(t)d_t \rvert ^2 \end{split}\end{equation}

sviluppando separatamente ambo i membri si ottiene

\begin{equation}\begin{split} a_1^2 a_2^2 + b_1^2 b_2^2 + a_1^2 b_2^2 + a_2^2 b_2^2 = \\ a_1^2 a_2^2 + b_1^2 b_2^2 + a_1^2 b_2^2 + a_2^2 b_2^2 \end{split}\end{equation}

l'unica combinazione possibile è che i due vettori siano paralleli.

Inoltre nella considerazione che la proprietà \(x^c(t) \rightarrow X^c(-f)\) :

\begin{equation}\begin{split} C_{12}(0)=\int_{-\infty}^{\infty} x_1(t)x_2^c(t)d_t= \int_{-\infty}^{\infty} F^{-1}[X_1(f)X_2^c(-f)] dt= \\ \int_{-\infty}^{\infty} X_1(f)e^{j2\pi f t} X_2^c(-f)e^{-j2\pi f t} dt= \\ \int_{-\infty}^{\infty} X_1(f)X_2^c(-f) d_f \end{split}\end{equation}

che altro non è che il Teo di Parsefal che indica che la quantità di energia nel dominio del tempo si conserva anche nel dominio della frequenza.

\begin{equation} \int_{-\infty}^{\infty} x_1(t)x_2^c(t)d_t=\int_{-\infty}^{\infty} X_1(f)X_2^c(-f)d_f \end{equation}

4.11. Autocorrelazione

Misura la velocità di variazione di un segnale e si definisce come :

\begin{equation} \label{orgdda76a2} A(\alpha)=(x_1(t)\star x_1^c(t))(\alpha)=\int_{-\infty}^{\infty} x_1(t + \alpha)x_1^c(\alpha)d_t \Rightarrow F[A(\alpha)]=S(f)=X_1(f)X_1^c(-f)=|X_1(f)|^2 \end{equation}

in cui \(\alpha\) rappresenta la finestra di covoluzione e \(S(f)\) è la la densità spettrale di energia.

Nel caso in cui \(\alpha=0\) si ottiene il teo dell'energia :
- se \(A(0)=0\) non è interessante;
- Nel caso in cui \(A(0) \neq 0\):
  \begin{equation} \label{org9d1284b} A(0)=\int_{-\infty}^{\infty} x_1(t)x_1^c(t)d_t=\int_{-\infty}^{\infty} \lvert x_1(t) \rvert ^2 d_t =E \end{equation}
  Dalla formula d'inversione della TDF si ha che :

\begin{equation}\begin{split} A(0)=\int_{-\infty}^{\infty} x_1(t)x_1^c(t)d_t=\int_{-\infty}^{\infty} F^{-1}[S_1(f)S_1^c(-f)] df=\\ \int_{-\infty}^{\infty} S_1(f)e^{j2\pi ft} S^c_1(f)e^{-j2\pi ft}d_t= \\ \int_{-\infty}^{\infty} S_1(f) S^c_1(-f)df= \\ \int_{-\infty}^{\infty} |S_1(f)|^2 d_f \end{split}\end{equation}

che altro non è che l'uguaglianza di Parsefal

\begin{equation} \label{orge414189} \int_{-\infty}^{\infty} \lvert x_1(t) \rvert ^2 d_t=\int_{-\infty}^{\infty} |X(f)|^2d_f \end{equation}

Nel caso \(\alpha \neq 0\) abbiamo le seguenti possibilità :
- \(A(0)=0\) non interessante;
- SE x(t) È COMPLESSO \(\Rightarrow A(\alpha)=A^C(-\alpha )\) SIMMETRIA HERMITIANA
- SE x(t) È REALE \(\Rightarrow A(\alpha)=A(-\alpha )\) SIMMETRIA REALE
Infine si ha che \(|A(\alpha)| \leqslant A(0)\)

5. Prontuario

funzione	\(\frac{1}{a + i 2 \pi f}\)
1	traformata
\(\delta(t)\)	1
c	1
\(sgn(t)\)	\(c\delta(t)\)
\(u(t)\)	\(\frac{1}{i 2 \pi f}\)
\(rect(t)\)	\(\frac{1}{i 2 \pi f} + \frac{\delta(f)}{2}\)
\(\frac{1}{t^n}\)	\(sinc(t)\) con \(f=0\) allora \(sinc(f)=1\)
\(sin(2\pi f_0 t)\)	\((-i)^n sgn(f)\frac{ \pi (2 \pi f)^{n-1}}{(n-1)!}\)
\(cos(2\pi f_0 t)\)	\(\frac{\delta(f -f_0)-\delta(f +f_0)}{2i}\)
\(t^n u(t)\)	\(\frac{\delta(f -f_0)+\delta(f +f_0)}{2i}\)
\(sin(2\pi f_0 t)u(t)\)	\(\frac{n!}{(i 2 \pi f)^{n+1}} + \frac{\delta(f) \cdot n!}{2 (i 2 \pi f)^n}\)
\(cos(2\pi f_0 t)u(t)\)	\(\frac{f_0}{2 \pi (f_0^2 – f^2)} + \frac{\delta(f – f_0) – \delta(f + f_0)}{4 i}\)
\(e^{at}u(t)\)	\(\frac{f_0}{2 \pi (f_0^2 – f^2)} + \frac{\delta(f – f_0) + \delta(f + f_0)}{4 }\)
\(te^{at}u(t)\)	\(\frac{1}{(a + i 2 \pi f)^2}\)
\(\sin(2 \pi f_0 t)u(t) e^{- a t}\)	\(\frac{2 \pi f_0}{(a + i 2 \pi f)^2 + 4 \pi^2 f_0^2}\)
\(\cos(2 \pi f_0 t)u(t) e^{- a t}\)	\(\frac{a + i 2 \pi f}{(a + i 2 \pi f)^2 + 4 \pi^2 f_0^2}\)
\(sinh(2\pi f_0)\)	\(\frac{1}{2} [\delta(f + i f_0) – \delta(f – i f_0)]\)
\(cosh(2\pi f_0)\)	\(\frac{1}{2} [\delta(f + i f_0) + \delta(f – i f_0)]\)