Trasformata Z
Table of Contents
- 1. Scopo
- 2. Dalla TDF alla TDZ
- 3. Convergenza della TDZ
- 4. Esempi di ROC
- 5. Trasformate Notevoli
- 6. Proprietà della TDZ
- 7. Antitrasformata della TDZ
- 8. Relazione di Parsefal per la TDZ
- 9. Link utili
1. Scopo
E' una trasformata complessa che si applica a funzioni discrete al fine di trasformarle in funzioni più semplici. Esiste in senso ordinario ( cioè senza ricorrere all'uso della delta di D. ) ed esiste anche quando non esiste la TDF. TDF e TDZ coincidono sul cerchio di raggio unitario vds \eqref{eq:1} e la TDF puo' essere considerata una restridione della TDZ.
Esempio :
La TDF di \(u(t)\) non esiste in senso ordinario in quanto è necessario utilizzare la \(\delta(t)\) per calcolare la TDF, mentre esiste la TDZ senza la delta di D.
Altro esempio di sequenza sono i segnali a pettine \(x(nT)=x[n]\)
2. Dalla TDF alla TDZ
Dalla definizione di cui alla \eqref{eq:101} si nota che la convergenza della serie si ha quando \(|x[n]|<1\) in quanto l'esponenziale e' sempre convergente
\begin{equation} \label{eq:101} \begin{split} X(F)=\sum_{n=-\infty}^{\infty} \tilde{x}[n] e^{-j2\pi n F} \end{split} \end{equation}per cui volendo rendere sempre convergente la serie dobbiamo moltiplicare \(x[n]\) per un fattore di smorzamento che tende a zero più rapidamente di come \(x[n] \rightarrow \infty\) di modo che \(|x[n](fattore\ di\ smorzamento)| \leq 1\) per cui abbiamo che \(\tilde{x}[n]=x[n](\frac{1}{r})^n\) in cui \(r\) e' noto come raggio di convergenza, dunque la \eqref{eq:101} diventa :
\begin{equation} \label{eq:1} \begin{split} ;\mathfrak{F}(\tilde{x}[n])=\mathfrak{F}(x[n]r^{-n})=\sum_{n=-\infty}^{\infty} \tilde{x}[n] e^{-j2\pi n F} = \\ = \sum_{n=-\infty}^{\infty}x[n] (\frac{1}{r})^n e^{-j2\pi nF}=\\ = \sum_{n=-\infty}^{\infty} x[n] (re^{j2\pi F})^{-n}= \\ = \color{red} \sum_{n=-\infty}^{\infty} x[n] z^{-n}=X(z) \end{split} \end{equation}Nel caso di \(x[n]\) sia una sequenza causale, cioè esiste un \(n=0\) t.c. \(x[n]=0 \ \forall \ n<0\) la \eqref{eq:1} diventa \(X(z)=\sum_{n=0}^{\infty} x[n] (re^{j2\pi ft})^{-n}\) nota come TDZ unilatera mentre altrimenti è nota come TDZ bilatera.
2.1. Criterio generale
Domanda : per quali valori di z si ha la convergenza della serie.
L'espressione della trasformata zeta è detta serie di Cauchy-Laurent. La regione di convergenza (ROC) della serie è il luogo dei punti per cui essa converge in modo uniforme ed e' una regione connessa. Nella regione di convergenza, la trasformata zeta è una funzione analitica, ossia continua e infinitamente derivabile con derivate continue.
La serie della trasformata zeta converge se e solo se la sequenza è assolutamente sommabile :
\begin{equation} \label{eq:102} \begin{split} |\sum_{n=-\infty}^{\infty}x[n]z^{-n}| \leq \sum_{n=-\infty}^{\infty}|x[n]||z^{-n}| \leq \sum_{n=-\infty}^{\infty}|x[n]|r^{-n} < \infty \end{split} \end{equation}Le regioni di convergenza nel piano complesso sono delimitate da circonferenze (ossia luoghi dei punti a modulo costante), perché non dipendono dalla fase ma solo dal modulo \(r\) e dunque :
- la parte anti-causale converge all'interno della circonferenza avente un raggio \(r_1\);
- la parte causale converge all'esterno di una circonferenza di raggio \(r_2\);
Da notare che per \(z=e^{j2\pi F}\) converge sulla circonferenza di raggio unitario in quanto considerando la notazione polare si puo' considerare l'esponenziale moltiplicato per il raggio unitario e di conseguenza l'interno del cerchio di raggio unitario e' il luogo dei punti in cui la TDZ converge mentre la circonferenza del predetto cerchio e' il luogo dei punti di convergenza della TDF in quanto per r=1 si ha che la definizione di TDZ coincide con quella di TDF.
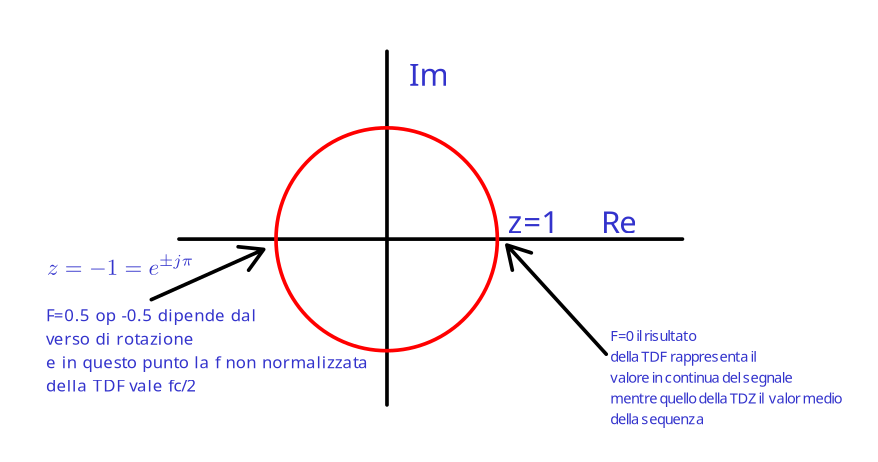
Figure 1: Cerchio di raggio unitario e suoi punti d'interesse
Nella figura seguente si riportano esempi di ROC ed esempi di sequenze
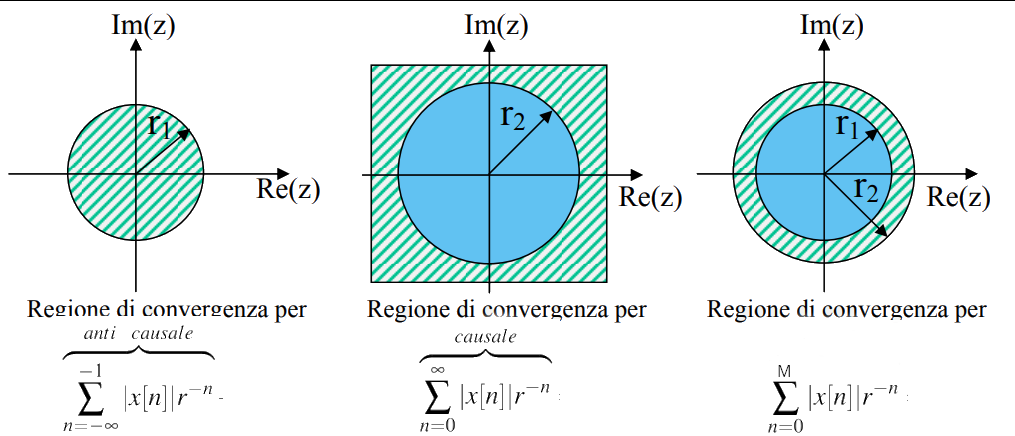
Figure 2: Esempi di ROC
3. Convergenza della TDZ
Quando la TDZ e' un rapporto di polinomi il raggio di convergenza è il reciproco del massimo valore assoluto dei poli ( radici del denominatore in cui vi è una discontinuità ) della TDZ.
Per determinare il raggio di convergenza, devi esaminare la trasformata Z specifica e identificare la posizione dei poli nella variabile complessa z.
3.1. ROC Interna
Si intende la regione del piano complesso interna al cerchio \(ROC=\{z: |z| < r \}\) in cui in cui \(r = max\{|z|\}\) senza includere il punto \(z=0\). Le sequenze del tipo unilatere destre ( sequenze anti-causali ). La convergenza sul bordo deve essere discussa di volta in volta.
3.2. ROC Esterna
Le sequenze del tipo unilatere sinistre ( sequenze causali ) convergono all'esterno del cerchio \(ROC_d\{z: |z| > r\}\) in cui \(r = max\{|z|\}\) (vds fig 6 ).
3.3. Corona Circolare
La ROC e' la parte di piano data dall'intersezione di \(ROC = ROC_s \cap ROC_d= \{z: r_s \leq |z| \leq r_d\}\) ed e' ottenuta con le sequenze bilatere . Nel caso di TDZ con piu' poli si ha \(r_{min} < |z| < r_{max}\). ( vds fig. nel seguito )
Figure 3: sequenza bilatera
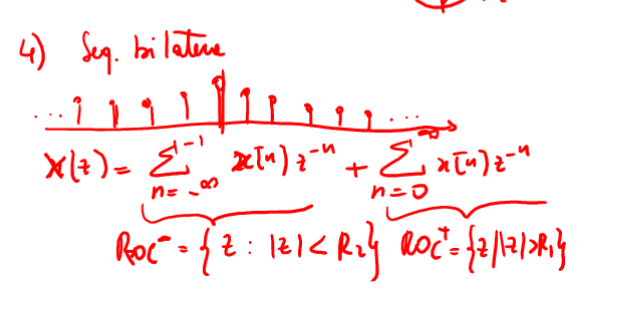
Figure 4: convergenza bilatera
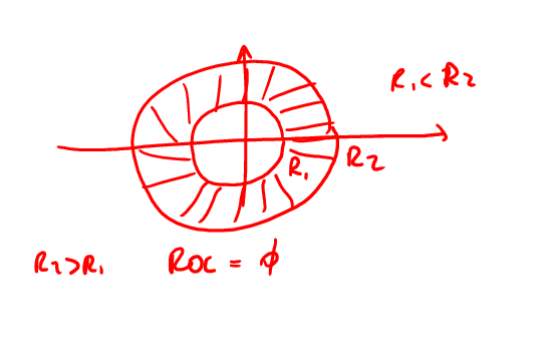
Figure 5: casi di ROC di una sequenza bilatera
3.4. ROC Miste
Sono considerate unilatere dx anche una sequenza con un numero finito di elementi a sx, in questo caso la convergenza è l'intersezione del piano z ( ROC per la parte finita ) e l'esterno del cerchio (ROC per la tdz dx ) che da come risultato la ROC della TDZ dx ( vds fig 7 ). In caso di poli multipli il raggio di convergenza e' il minimo tra tutti i poli;
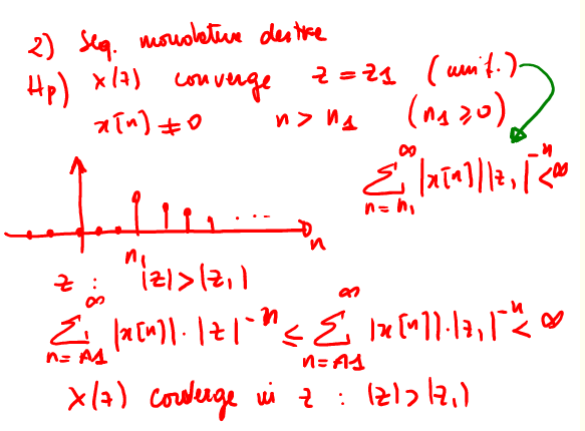
Figure 6: dimostrazione della convergenza unilatera dx
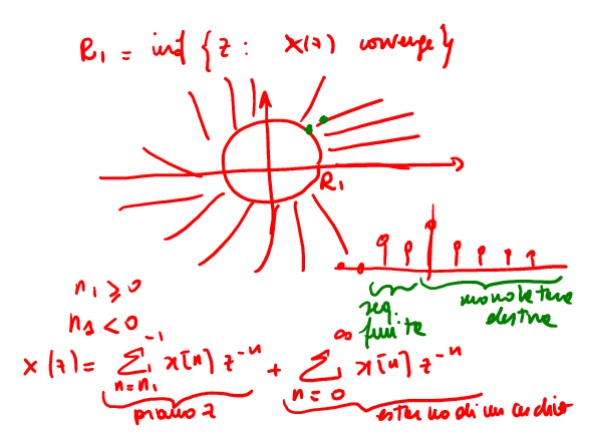
Figure 7: caso particolare di convergenza unilatera dx
3.5. Intero piano complesso
Quanto la TDZ non rappresenta dei poli le sequenze finite da cui deriva convergono su tutto il piano z anche se per alcune sequenze ci possono essere dei problemi in punti particolari vds fig 8. Inoltre se la sequenza e' :
- Sequenza unilatera causale. La trasformata zeta converge in qualunque punto del piano complesso eccetto l'origine. La regione di convergenza è all'esterno di una circonferenza di raggio infinitesimo.
- Sequenza unilatera anti-causale. La trasformata zeta converge in qualunque punto nel piano complesso eccetto l'infinito. La regione di convergenza è all'interno di una circonferenza di raggio infinito.
- Sequenza bilatera. La trasformata zeta converge in qualunque punto nel piano complesso eccetto l'origine e l'infinito.
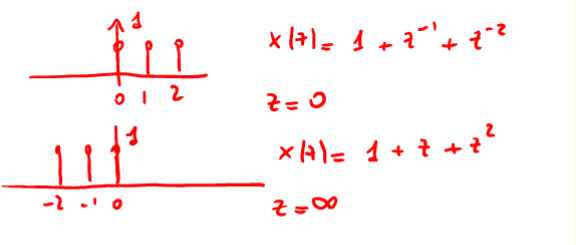
Figure 8: casi di esclusione di z per sequenze finite.
4. Esempi di ROC
4.1. Impulso discreto
Sia \(x[n]=\delta[n]\) allora la sua TDZ vale
\begin{equation} \label{eq:100hh1} \begin{split} X(z)=\sum_{n=-\infty}^{\infty}\delta[n] z^{-n}=1 \end{split} \end{equation}la ROC e' l'intero piano complesso.
4.2. gradino \(u[n]\)
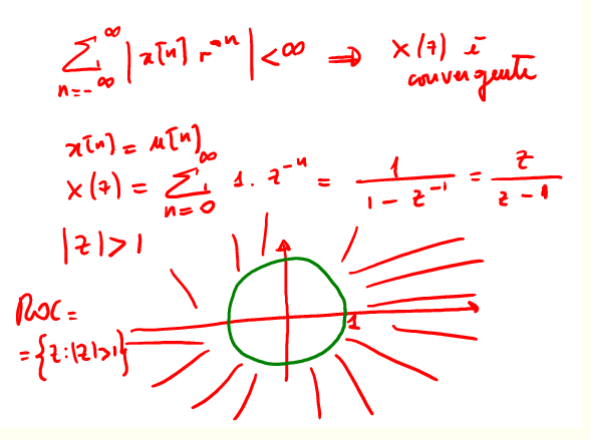
Figure 9: studio della ROC di \(u[n]\)
5. Trasformate Notevoli
5.1. Esponenziale \(x[n]=a^nu[n]\)
Con \(a\) anche numero complesso. Dalla TDZ il polo del denominatore e' \(a\) e considerato che si tratta una un sequenza causale la ROC e' la regione di piano esterna al cerchio di raggio \(|a|\).
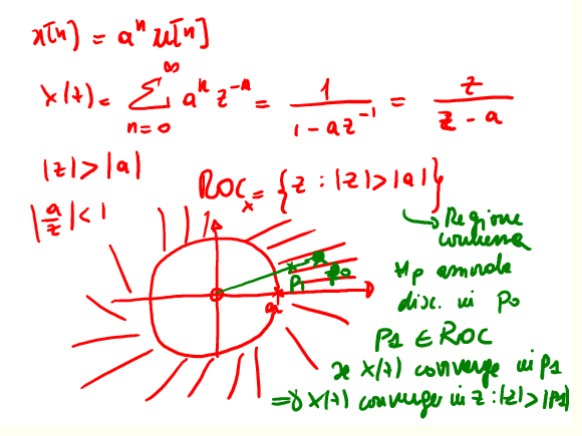
Figure 10: esempio della sequenza \(a^nu[n]\)
5.1.1. Esempio \(2^nu[n]\)
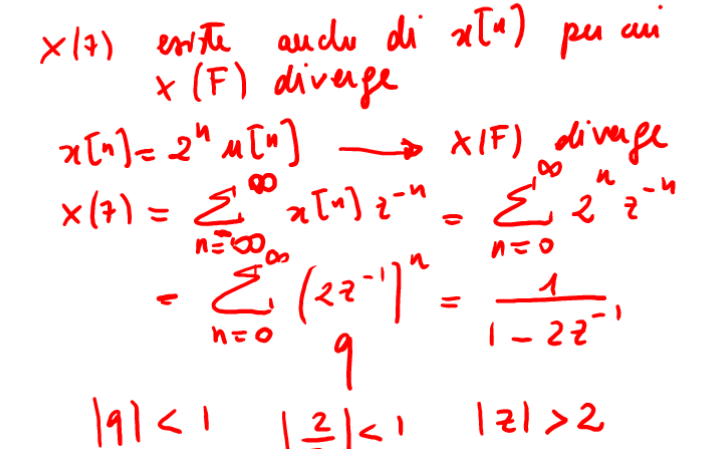
Figure 11: funzione \(2^nu[n]\)
la cui regione di convergenza è quella esterna al cerchio di raggio 2 mentre il cerchio di raggio unitario (regione di conv della TDF ) non è compreso all'interno della ROC della TDZ ed è per questo che la TDF non converge
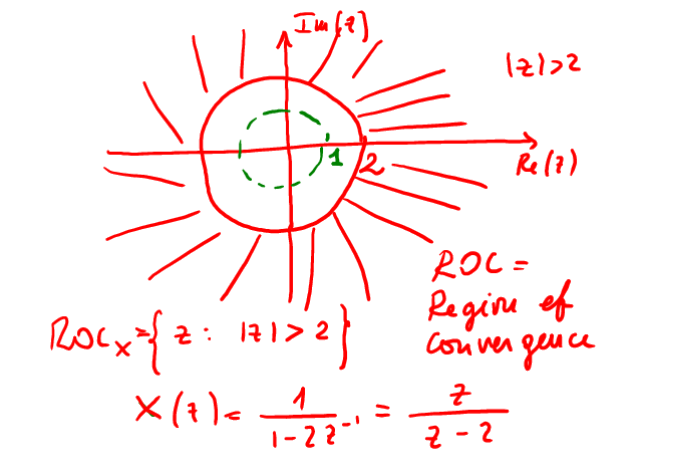
Figure 12: ROC di \(2^nu[n]\)
5.2. Esponenziale Invertito \(x[n]=-a^{-n}u[n-1]\)
Sequenza fondamentale. Da notare che la TDZ è quella dell'esempio precedente ma con ROC diversa in quanto si tratta di una sequenza anti-causale.
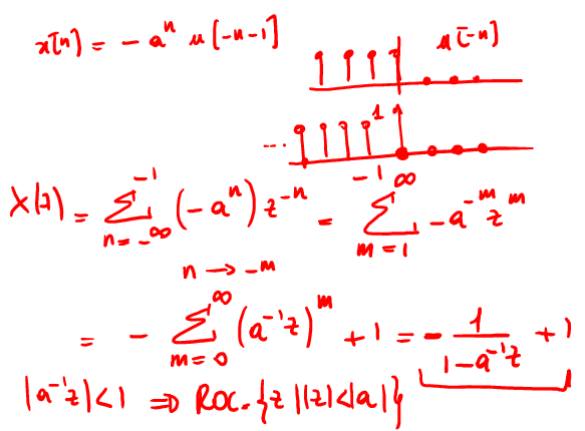
Figure 13: calcolo della TDZ di \(x[n]=-a^{-n}u[n-1]\)
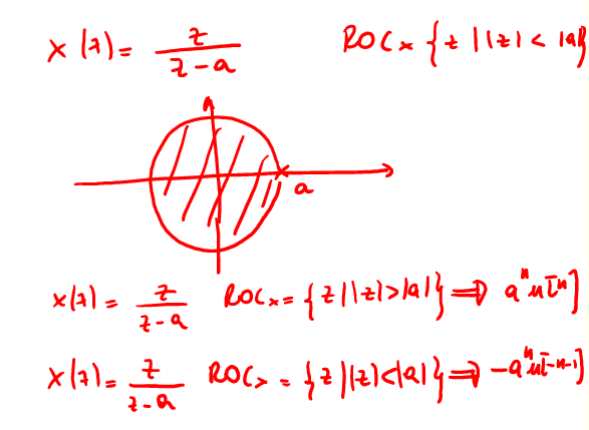
Figure 14: calcolo della ROC di \(x[n]=a^{-n}u[n-1]\)
5.3. TDZ di funzioni periodiche
Sia \(x_p[n]\) la funzione periodica generata da
\begin{equation}\begin{split} \label{orgf78ac76} x_N[n]= \begin{cases} x_p[n] & 0 \leq n < N \\ 0 & altrove \end{cases} \end{split}\end{equation}allora la TDZ della funzione periodica
\begin{equation}\begin{split} \label{org308a5b7} X_p(z)=\frac{z^p}{z^p -1 }X_N(z) \end{split}\end{equation}5.3.1. Esempio
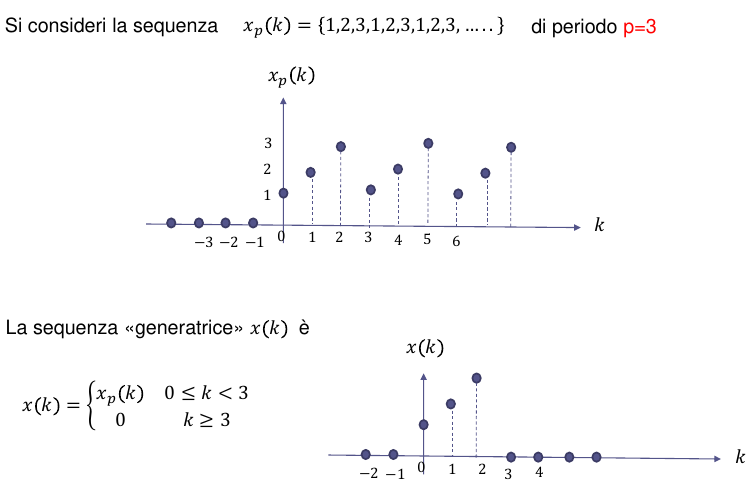
Figure 15: Esempio p. 1 di TDZ di funzione periodica

Figure 16: Esempio p. 2 di TDZ di funzione periodica
6. Proprietà della TDZ
6.1. Ritardo o Traslazione
Sia \(\tilde{x}[n]=x[n-n_0]\) e si indichi \(k=n -n_0\) allora
\begin{equation} \label{org1bf43bf} \begin{split} \tilde{X(z)}=\sum_{n=-\infty}^{\infty} \tilde{x}[n]z^{-n}= \\ \sum_{n=-\infty}^{\infty} x[n-n_0]z^{-n}= \\ \sum_{k=-\infty}^{\infty} x[k]z^{-(k + n_0)}=\\ z^{-n_0} \sum_{k=-\infty}^{\infty} x[k]z^{-k} \end{split} \end{equation}NB : il raggio di convergenza di \(\tilde{X}[f]\) è lo stesso di \(X[f]\) a meno :
- dello 0 quando \(n_0 \geqslant 0\);
del punto all' \(\infty\) quando \(n_0 \leq 0\);
Inoltre la proprietà si può applicare quando tutte le sequenze hanno lo stesso ritardo.
6.2. Derivazione nel dominio del tempo discreto
Sia \(\tilde{x}[n]=nx[n]\) allora \(\tilde{X}(z)=-z \frac{d}{d_z} X(z)\)
6.2.1. Dimostrazione
6.3. Derivazione nel dominio z
\(\frac{d}{dz}X(z) = -z^{-1}\tilde{X}(z)\) con \(\tilde{X}(z)=\mathbb{TDZ}(nx[n])\)
6.3.1. Dimostrazione
6.4. Convoluzione
sia \(\tilde{x}[n]=x[n] \bigotimes y[n]\) e sia \(\alpha=n-k \rightarrow n=k + \alpha\) allora
\begin{equation}\begin{split} \tilde{X}(z)=\sum_{n=-\infty}^{\infty} \tilde{x}[n]z^{-n}=\sum_{k=-\infty}^{\infty}\sum_{n=-\infty}^{\infty}x[k]y[n-k]z^{-n}=\\ \sum_{k=-\infty}^{\infty}x[k]\sum_{\alpha = -\infty}^{\infty}x[\alpha]z^{-\alpha -k}=\\ \sum_{k=-\infty}^{\infty} x[k] z^{-k} \sum_{\alpha = -\infty}^{\infty} y[\alpha] z^{-\alpha}=X(z)Y(z)\\ \end{split}\end{equation}la zona di convergenza è l'intersezione delle zone di convergenza.
6.5. Prodotto
\(y[n]=x[n]w[n] \leftrightarrow Y(z)=X(z)*W(z)\)
6.6. Coniugazione
\(y[n]=x^c[n] \leftrightarrow y[z]=x^c[z^c]\) in cui entrambe le uguaglianze hanno la stessa regione di convergenza
6.7. Inversione temporale
\(y[n]=x[-n] \leftrightarrow y(z)=x(z^{-1})\) con \(ROC=\{z: 1/r_1<|z|<1/r_2\}\) con \(r_1,r_2\), rispettivamente gli estremi inferiori e superiori della regione di convergenza della \(X(z)\).
6.8. Convoluzione Complessa
Sia \(w[n]=x[n]y[n]\) allora la covoluzione complessa risulta :
\begin{equation}\begin{split} \label{org6303821} W(z)=\frac{1}{j2\pi}\oint_C Y(z)X(\frac{z}{v})v^{-1}dv \end{split}\end{equation}6.8.1. Dimostrazione
Dal risultato della \eqref{eq:07} abbiamo il seguente risultato preliminare
\begin{equation} \label{eq:10002} y[n]=\frac{1}{j2\pi}\oint_C Y(v)v^{v-1}d_v \end{equation} \begin{equation} \label{eq:1004} \begin{split} W[z]=\sum_{n=-\infty}^{\infty} x[n]y[n]z^{-n}=\sum_{n=-\infty}^{\infty} x[n] \frac{1}{j2\pi}\oint_C Y(v)v^{v-1}d_v= \\ \frac{1}{j2\pi}\oint_C Y(v)v^{v-1} (\sum_{n=-\infty}^{\infty} x[n] z^{-n})d_v = \frac{1}{j2\pi}\oint_C Y(v) (\sum_{n=-\infty}^{\infty} x[n] v^{v-1}z^{-n})d_v= \\ \frac{1}{j2\pi}\oint_C Y(v) (\sum_{n=-\infty}^{\infty} x[n] (\frac{z}{v})^{-n}v^{-1})d_v= \frac{1}{j2\pi}\oint_C Y(v) X(\frac{z}{v})v^{-1}d_v \end{split} \end{equation}6.8.2. Raggio di convergenza
Nell'ipotesi che la covoluzione complessa converga allora il percorso C è incluso nelle ROC di X(z/v) e Y(v) le rispettive ROC sono :
- \(ROC_X = \{z: R_{1X} < |z| < R_{2X}\}\);
- \(ROC_Y = \{z: R_{1Y} < |z| < R_{2Y}\}\);
Nel caso di specie le ROC di x[n] e y[n] sono
- \(R_{1X} < |v| < R_{2X}\);
- \(R_{1Y} < |z/v| < R_{2Y}\);
e la ROC di W(z) appartiene all'intersezione ( prodotto delle zone ) delle due zone di convergenza :
- \(R_{1X}R_{1Y} <|z| < R_{2X}R_{2Y}\)
Applicando la normalizzazione alle sequenze x[n] e y[n] e nell'ipotesi che queste ammettono entrambe TDF allora le loro ROC comprendono la circonferenza unitaria, che altro non è che il cammino d'integrazione, per cui :
- all'interno della circonferenza unitaria \(z=e^{j2\pi F}\)
- lungo il cammino d'integrazione (circonferenza unitaria ) \(v=e^{j2\pi \theta}\)
- \(d_v=j2\pi e^{j2\pi \theta}d_{\theta}\)
- \(-0.5 < F < 0.5\)
per cui la \eqref{eq:1004} può essere riscritta, in funzione anche del fatto che \((z/v)=zv^{-1}=e^{j2\pi F}e^{-j2\pi \theta}=e^{-j2\pi (F-\theta)}\) da cui \(X(z/v)=X(F- \theta)\)
\begin{equation}\begin{split} \label{org1b6b8e8} W(z)=\frac{1}{j 2\pi}\int_{-0.5}^{0.5}Y(\theta)X(F - \theta) e^{-j2\pi \theta} j2\pi e^{j2\pi \theta} d_{\theta} \end{split}\end{equation}7. Antitrasformata della TDZ
L'operazione di inversione associa ad una funzione di variabile complessa definita un una precisa regione di piano una sequenza \(x[n]\), si noti che diverse sequenze hanno la stessa TDZ e dunque per ottenere l'inversione è necessario conoscere l'insieme di convergenza.
7.1. Definizioni
- Polo radici che annullano il denominatore di \(D(z)\), E un punto di discontinuità. Non ci sono poli all'interno della ROC;
- Zeri radici che annullano il numeratore di \(N(z)\). Non è punto di discontinuità;
- Teo integrale di Cauchy
in cui \(C\) è una curva chiusa contenente l'origine e percorsa in senso antiorario.
Residuo : e' il coeficente della serie di Laurent che approssima \(X(z)\) nell'intorno di un polo \(z_i\). Sia \(Y(z)\) una funzione complessa con polo \(z_i\) interno alla regione di convergenza di molteplicità \(m\) allora il residuo della funzione nell'intorno del polo vale :
\begin{equation}\begin{split} \label{orgc1e2ca4} Res[X(z), z_i]= \left. \frac{1}{(m-1)!} \lim_{z \rightarrow z_i}\frac{d^{m-1}}{d_z^{m-1}}[X(z)(z-z_i)^m] \right|_{z=z_i} \end{split}\end{equation}
7.2. Metodo d'inversione con il metodo del Teorema dei Residui
7.2.1. Dimostrazione
per cui
\begin{equation} \label{eq:07} x[n]=\frac{1}{j2\pi} \int_C X(z)z^{n-1} d_z \end{equation}7.3. Metodo d'inversione con la forma frazionaria
Sia S\(X(z)=\frac{N(z)}{D(z)}\) una funzione complessa esprimibile in forma frazionaria per la risoluzione si ricorre al metodo dei fratti semplici calcolando i poli
\begin{equation} \label{eq:001} X(z)=\frac{N(z)}{D(z)} \rightarrow \frac{X(z)}{z}=\frac{N(z)}{zD(z)} \end{equation}calcolo i poli della \eqref{eq:001} e ottengo due casi :
7.3.1. poli semplici
t.c. il generico polo si calcola
\begin{equation}\begin{split} \label{org9d48d4b} A_n = \left. X(z)\frac{(z-a_n)}{z} \right |_{z=a_n} \end{split}\end{equation}per cui dopo aver calcolato tutti i termini \(A\) ottengo
\begin{equation} \label{eq:003} X(z)=z\frac{A_0}{z-a_0} + \cdots +z\frac{A_n}{z-a_n} \end{equation}in cui ognuno dei termini vale, a seconda della ROC, \(a^nu[n]\) op. \(-a^nu[-n-1]\) ( vds esempi precedenti )
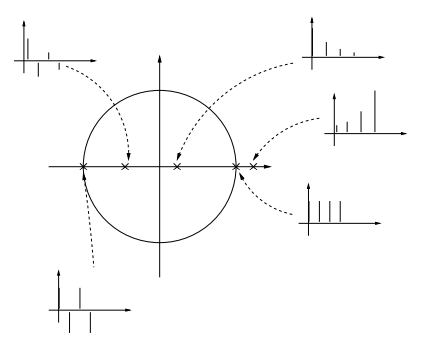
Figure 17: Poli reali e segnali per trasformate razionali
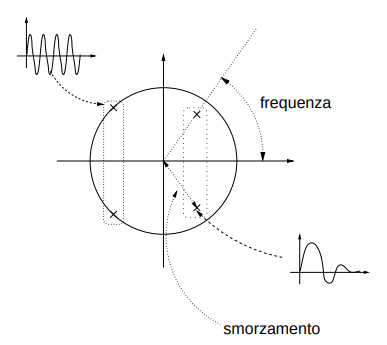
Figure 18: Poli complessi e segnali per trasformate razionali
7.3.2. poli di molteplicità \(m\)
in cui il generico termine \(A_{ij}\)
\begin{equation}\begin{split} \label{org721a0be} A_{ij}= \frac{1}{(p-j)!} \frac{d^{p-j}}{d^{p-j}_z} \left. ( \frac{X(z)}{z}(z-a_i)^p ) \right |_{z=a_i} \end{split}\end{equation}dove l'indice \(i=0\) significa l'assenza di derivazione. In pratica
\(x(n)=\sum Residui\ dei\ poli\ di X(z)z^{n-1}\ in\ C\)
7.4. Esempi
7.4.1. Poli semplici
Nella fig. 20 c'è da notare che per il calcolo dell'antitrasformata devo trovare tutte le ROC connesse di ogni singola frazione che compone la X(z) e poi suddividere il piano in sottoinsiemi sui quali calcolare tutte le possibili antitrasformate e nel caso di specie si ha :
- \(ROC_1\) : piano z esterno al cerchio con \(|z|>2\); l'antitrasformata del primo termine è una \(\delta[n]\), il secondo ed il terzo sono monolatere dx;
- \(ROC_2\) : piano esterno al cerchio \(|z|>1/3\); l'antitrasformata del primo termine è una \(\delta[n]\), il secondo è una monolatera dx e il terzo una monolatera sx perché interna al cerchio di raggio 2;
- \(ROC_3\) : piano interno al cerchio \(|z|<1/3\); l'antitrasformata del primo termine è una \(\delta[n]\), il secondo ed il terzo sono monolatere sx;
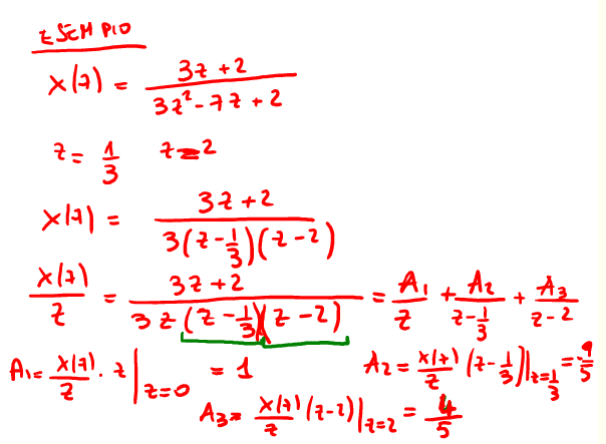
Figure 19: calcolo dell'inversa della TDZ - no ROC
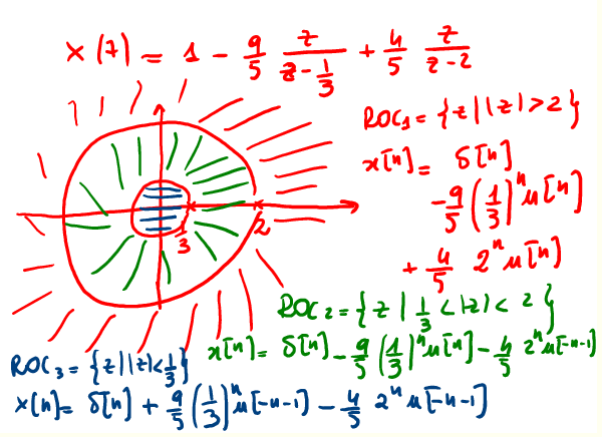
Figure 20: calcolo della ROC dell'inversa della TDZ
7.4.2. Poli multipli
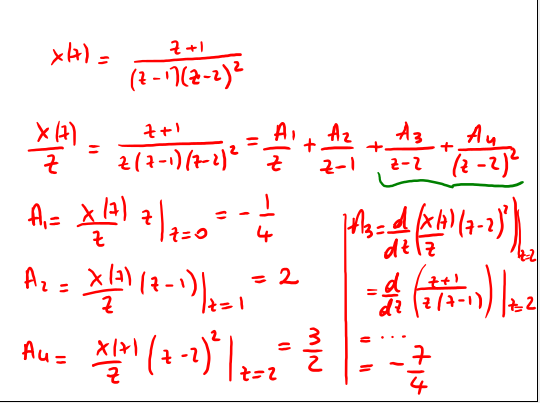
Figure 21: esempio di scomposizione in fattori con poli multipli
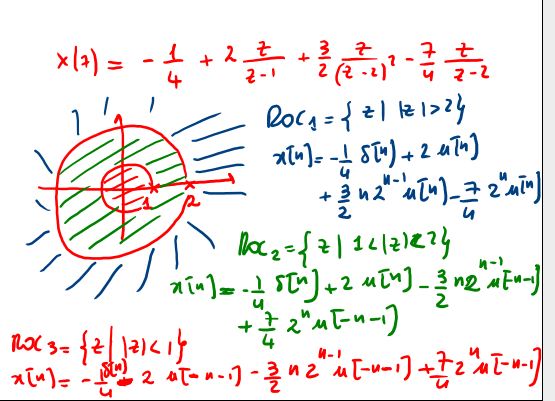
Figure 22: ROC della TDZ con poli multipli
8. Relazione di Parsefal per la TDZ
Applicando alla relazione \eqref{eq:1004} la definizione del teo di Parsefal \(w[n]=x[n]y^c[n]\) e per la proprietà della coniugazione si ha che :
\begin{equation} \label{eq:1202} \sum_{n=-\infty}^{\infty}x[n]y^c[n]=\frac{1}{j2\pi}\oint_CX(v)Y^c(z^c / v^c )v^{-1}d_v \end{equation}nella considerazione che z=1 in quanto ….. e con \(v=e^{j2\pi \theta}\) la \eqref{eq:1202} abbiamo :
\begin{equation} \label{eq:1203} \sum_{n=-\infty}^{\infty}x[n]y^c[n]=\frac{1}{j2\pi}\oint_CX(v)Y^c(1 / v^c )v^{-1}d_v = \\ \frac{1}{j2\pi}\oint_CX(\theta)Y^c(\theta )d_{\theta} \end{equation}inoltre nel caso che \(x[n]=y[n]\) abbiamo che la \eqref{eq:1203} diventa :
\begin{equation} \label{eq:1204} \sum_{n=-\infty}^{\infty}|x[n]|^2=\frac{1}{j2\pi}\oint_c X(v)X^c(1/v^c )v^{-1}d_v \end{equation}Nel caso di variabili reali la \eqref{eq:1203} e la \eqref{eq:1204} diventano
\begin{equation} \label{eq:1205} \sum_{n=-\infty}^{\infty}x[n]y^c[n]=\frac{1}{j2\pi}\oint_C X(v)Y^c(v^{-1})v^{-1}d_v \end{equation}inoltre nel caso che \(x[n]=y[n]\) abbiamo che la \eqref{eq:1203} diventa :
\begin{equation} \label{eq:1206} \sum_{n=-\infty}^{\infty}|x[n]|^2=\frac{1}{j2\pi}\oint_c X(v)X^c(v^{-1})v^{-1}d_v \end{equation}