Analisi 2 - Integrali in \(R^2\) con domini parametrici
Table of Contents
1. Introduzione
sia \(\iint_A f(\vec{x})d\vec{A}\) l'integrale della funzione \(f:A \subseteq \mathbb{R}^n \rightarrow \mathbb{R}\) definita sul dominio \(A\)
allora mediante opportune trasformazioni sulle funzioni descrittive del dominio \(A\) l'integrale puo' essere riscritto come
\(\iint_A f(\vec{x})d\vec{A}\) \(\rightarrow\) \(\iint_B f(\vec{y}) J(\vec{y}) d\vec{y}\)
in cui \(J(\vec{y})\) e' lo jacobiano della matrice di trasformazione che rappresenta il prezzo pagare.
2. Definizione
Sia \((x, y)\) un sistema di coordinate cartesiane nel piano, e consideriamo una trasformazione differenziabile e invertibile:
\begin{equation}\begin{split} \begin{cases} x = x(u, v) \\ y = y(u, v) \end{cases} \quad \text{con } (u,v) \in D' \end{split}\end{equation}Allora, per una funzione \(f(x,y)\), l’integrale su un dominio \(D \subset \mathbb{R}^2\) si può trasformare come:
\[ \iint_D f(x, y) \, dx\,dy = \iint_{D'} f(x(u, v), y(u, v)) \cdot \left| \det J(u, v) \right| \, du\,dv \]
dove \(J(u, v)\) è il jacobiano della trasformazione:
\begin{equation}\begin{split} J(u, v) = \begin{pmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{pmatrix} \quad \Rightarrow \quad \left| \det J(u,v) \right| = \left| \frac{\partial(x, y)}{\partial(u, v)} \right| \end{split}\end{equation}3. Esempio
Vogliamo calcolare questo integrale doppio:
\[ \iint_D (x + y)\, dx\,dy \]
dove il dominio \(D\) è il triangolo con vertici:
- \((0,0)\),
- \((1,0)\),
- \((0,1)\)
Quindi \(D\) è questo triangolo rettangolo nel primo quadrante:
(0,1) ●
|\
| \
| \
| \
| \
●-----● (1,0)
(0,0)
In coordinate \(x, y\), il dominio è descritto da:
\[ D = \{ (x, y) \in \mathbb{R}^2 \mid x \in [0,1], y \in [0, 1 - x] \} \]
3.1. Cambio di variabili
Poniamo il cambio:
\begin{equation}\begin{split} \begin{cases} u = x + y \\ v = x \end{cases} \Rightarrow \begin{cases} x = v \\ y = u - v \end{cases} \end{split}\end{equation}➡️ Questo cambio di variabili serve a semplificare l'integrando: \(x + y = u\), quindi la funzione \(f(x, y) = x + y\) diventa semplicemente \(f(u,v) = u\).
3.2. Jacobiano
Dobbiamo calcolare il determinante jacobiano della trasformazione inversa (cioè \(x = v,\ y = u - v\)):
\begin{equation}\begin{split} J = \frac{\partial(x, y)}{\partial(u, v)} = \begin{pmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & -1 \end{pmatrix} \end{split}\end{equation}\[ \Rightarrow \det(J) = (0)(-1) - (1)(1) = -1 \Rightarrow |\det J| = 1 \]
3.3. Nuovo dominio \(D'\)
Ora traduciamo il triangolo \(D\) in coordinate \((u,v)\):
Sappiamo che:
- \(x = v \in [0,1]\)
- \(y = u - v \ge 0 \Rightarrow u \ge v\)
- Inoltre \(y \le 1 - x = 1 - v \Rightarrow u - v \le 1 - v \Rightarrow u \le 1\)
Quindi il nuovo dominio è:
\[ D' = \{ (u,v) \in \mathbb{R}^2 \mid 0 \le v \le u \le 1 \} \]
È un triangolo anche in \((u,v)\), più facile da gestire:
u ↑ 1 |———● | / | / | / |/ 0 ●——————→ v 0 1
3.4. Nuovo integrale
Ora riscriviamo l’integrale:
\[ \iint_D (x + y) \, dx\,dy = \iint_{D'} u \cdot 1 \, dv\,du \]
(1 è il valore assoluto del determinante Jacobiano)
Integro prima in \(v\), poi in \(u\):
\[ = \int_{u=0}^1 \int_{v=0}^u u\, dv\, du \]
Dentro l'integrale \(u\) è costante rispetto a \(v\), quindi:
\[ = \int_0^1 u \cdot (u - 0)\, du = \int_0^1 u^2\, du = \left[ \frac{u^3}{3} \right]_0^1 = \frac{1}{3} \]
3.5. Risultato finale:
\[ \boxed{\iint_D (x + y)\, dx\,dy = \frac{1}{3}} \]
4. Esempio
Calcolare:
\[ I = \iint_D (x^2 - y^2)\, dx\,dy \]
dove \(D\) è la regione racchiusa tra le iperboli:
\[ xy = 1,\quad xy = 4 \]
e le rette:
\[ x/y = 1,\quad x/y = 2 \]
4.1. Passo 1: Analisi del dominio
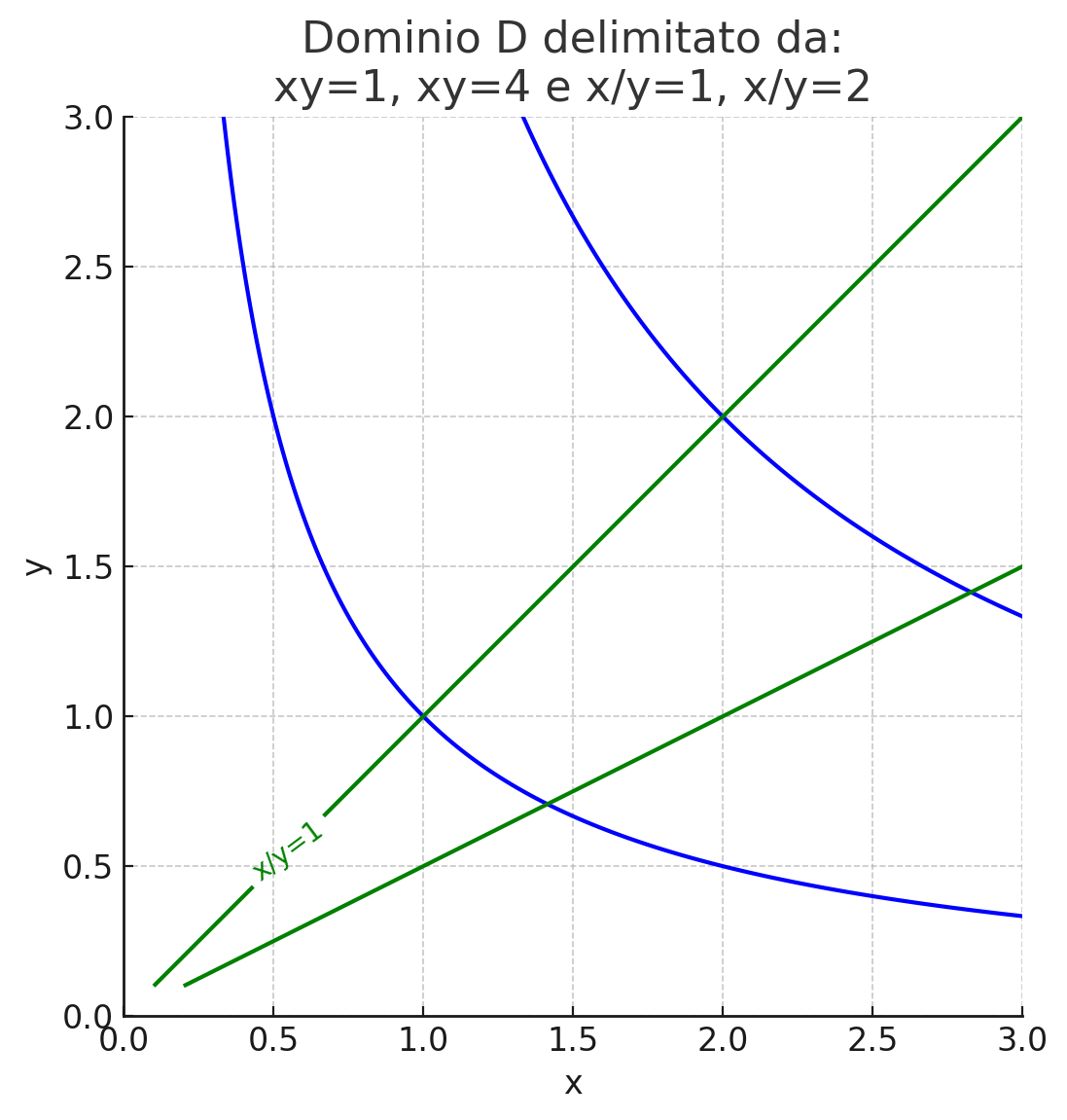
Figure 1: rappresentazione del dominio
Ecco il grafico del dominio \(D\):
- Le curve blu sono le iperboli \(xy = 1\) e \(xy = 4\)
- Le curve verdi sono le rette \(x/y = 1\) e \(x/y = 2\)
Il dominio \(D\) è l’area racchiusa tra queste 4 curve: una sorta di curvilineo a forma di trapezio nel primo quadrante.
Vediamo meglio:
- Le curve \(xy = \text{costante}\) sono iperboli: fissano il prodotto \(xy\).
- Le curve \(x/y = \text{costante}\) sono rette passanti per l'origine con diverse inclinazioni: fissano il rapporto \(x/y\).
Quindi possiamo pensare al cambio di variabili:
\begin{equation} \begin{cases} u = xy \\ v = \frac{x}{y} \end{cases} \end{equation}4.2. Passo 2: Troviamo la trasformazione inversa
Troviamo \(x\) e \(y\) in funzione di \(u\) e \(v\):
\[ v = \frac{x}{y} \Rightarrow x = v y \]
Sostituendo in \(u = xy\):
\[ u = (v y)y = v y^2 \Rightarrow y^2 = \frac{u}{v} \Rightarrow y = \sqrt{\frac{u}{v}} \]
Quindi:
\begin{equation} \begin{cases} y = \sqrt{\frac{u}{v}} \\ x = v y = v \sqrt{\frac{u}{v}} = \sqrt{u v} \end{cases} \end{equation}(Teniamo solo i valori positivi perché il dominio è nel primo quadrante.)
4.3. Passo 3: Jacobiano
Ora calcoliamo il jacobiano della trasformazione inversa, cioè:
\[ J = \left| \frac{\partial(x, y)}{\partial(u, v)} \right| \]
Calcoliamo le derivate parziali di \(x = \sqrt{u v}\) e \(y = \sqrt{u/v}\):
Derivate di \(x = \sqrt{uv}\):
\[ \frac{\partial x}{\partial u} = \frac{1}{2} \cdot \frac{v}{\sqrt{uv}}, \quad \frac{\partial x}{\partial v} = \frac{1}{2} \cdot \frac{u}{\sqrt{uv}} \]
Derivate di \(y = \sqrt{u/v}\):
\[ \frac{\partial y}{\partial u} = \frac{1}{2} \cdot \frac{1}{\sqrt{u v}}, \quad \frac{\partial y}{\partial v} = -\frac{1}{2} \cdot \frac{u}{v^2 \sqrt{u/v}} = -\frac{1}{2} \cdot \frac{\sqrt{u}}{v^{3/2}} \]
Ma è più semplice calcolare il jacobiano diretto, da \((x,y) \mapsto (u,v)\):
\begin{equation} \begin{cases} u = x y \\ v = x/y \end{cases} \Rightarrow J = \begin{pmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{pmatrix} = \begin{pmatrix} y & x \\ \frac{1}{y} & -\frac{x}{y^2} \end{pmatrix} \end{equation}\[ \det J = y \cdot \left(-\frac{x}{y^2}\right) - x \cdot \frac{1}{y} = -\frac{x}{y} - \frac{x}{y} = -\frac{2x}{y} \]
\begin{equation} |J| = \left| -\frac{2x}{y} \right| = \frac{2x}{y} = 2v \quad \text{(perché } x/y = v) \end{equation}4.4. Passo 4: Cambiamo l'integrale
Ricorda:
- \(x^2 - y^2 = (\sqrt{uv})^2 - \left(\sqrt{u/v}\right)^2 = uv - \frac{u}{v}\)
- Il jacobiano in valore assoluto è \(2v\)
Quindi l'integrale diventa:
\[ I = \iint_{D'} \left(uv - \frac{u}{v} \right) \cdot 2v\, du\,dv = \iint_{D'} \left(2uv^2 - 2u \right)\, du\,dv \]
4.5. Passo 5: Nuovo dominio \(D'\)
Nel cambio:
- \(u = xy \in [1, 4]\)
- \(v = x/y \in [1, 2]\)
Quindi \(D'\) è il rettangolo:
\[ D' = \{ (u,v) \mid u \in [1,4],\ v \in [1,2] \} \]
4.6. Passo 6: Calcolo integrale
\[ I = \int_{v=1}^{2} \int_{u=1}^{4} \left(2uv^2 - 2u\right) du\,dv = \int_1^2 \left[ 2v^2 \int_1^4 u\, du - 2 \int_1^4 u\, du \right] dv \]
Calcoliamo:
\[ \int_1^4 u\, du = \left[ \frac{u^2}{2} \right]_1^4 = \frac{16 - 1}{2} = \frac{15}{2} \]
Quindi:
\[ I = \int_1^2 \left[ 2v^2 \cdot \frac{15}{2} - 2 \cdot \frac{15}{2} \right] dv = \int_1^2 \left(15v^2 - 15\right)\, dv = 15 \int_1^2 (v^2 - 1)\, dv \]
\[ = 15 \left[ \frac{v^3}{3} - v \right]_1^2 = 15 \left( \left( \frac{8}{3} - 2 \right) - \left( \frac{1}{3} - 1 \right) \right) = 15 \left( \frac{2}{3} + \frac{2}{3} \right) = 15 \cdot \frac{4}{3} = \boxed{20} \]
4.7. Risultato finale:
\[ \boxed{\iint_D (x^2 - y^2)\, dx\,dy = 20} \]