Analisi 2 - Coordinate sferiche in \(R^3\)
Table of Contents
1. Definizione del sistema di coordinate sferiche
Un punto nello spazio è descritto da tre coordinate:
- \(r\) — raggio (distanza radiale): distanza del punto dall'origine.
- \(\theta\) — angolo polare o colatitudine: angolo tra il vettore posizione e l'asse \(z\) (varia da \(0\) a \(\pi\)).
- \(\varphi\) — angolo azimutale: angolo tra la proiezione del punto sul piano \(xy\) e l’asse \(x\) (varia da \(0\) a \(2\pi\)).
Le coordinate sferiche sono quindi: \((r, \theta, \varphi)\)
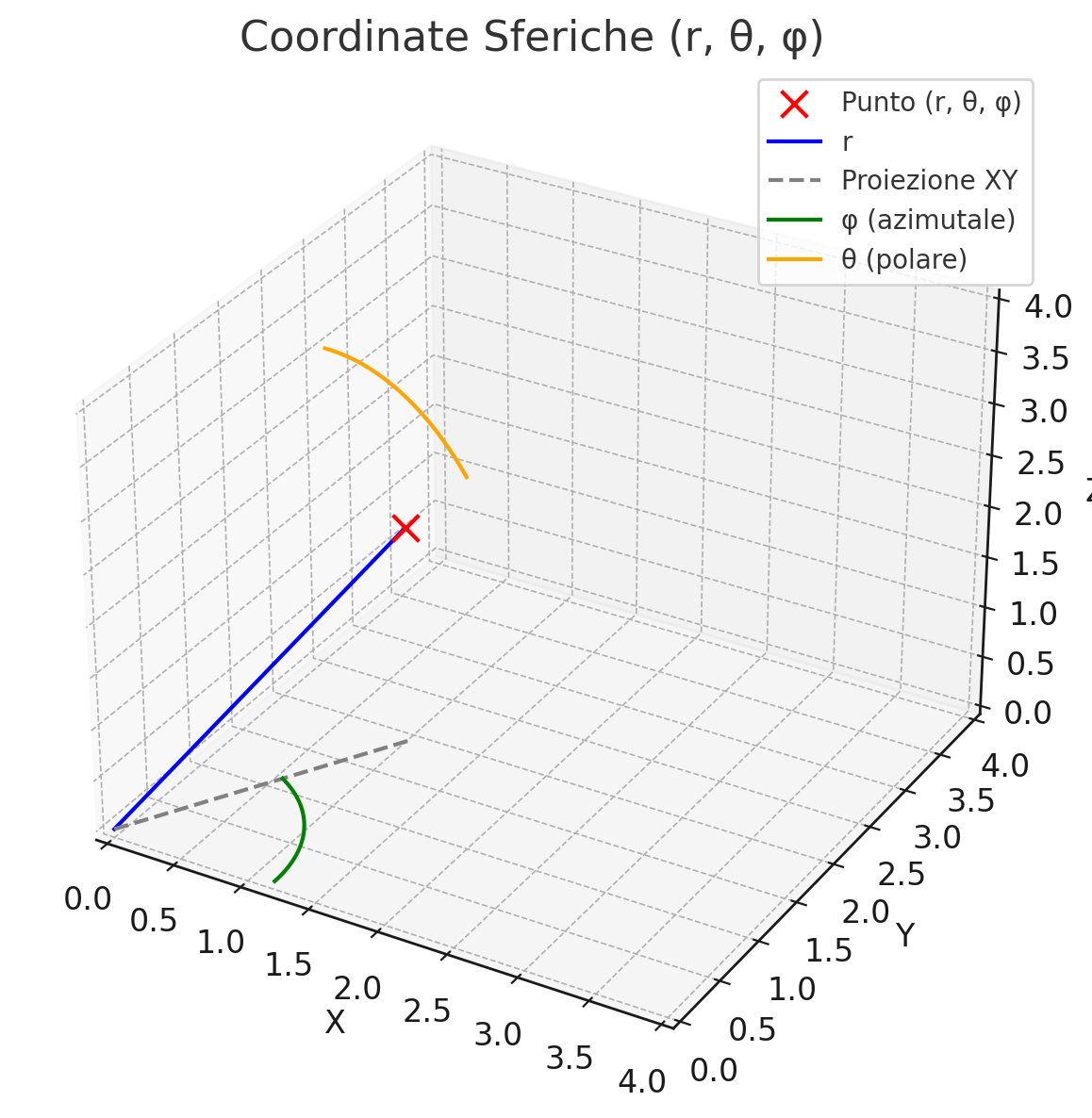
Figure 1: rappresetazione delle definizioni
Ecco un diagramma che mostra un punto in coordinate sferiche su un sistema 3D:
- Punto rosso: rappresenta il punto nello spazio.
- Linea blu: la distanza radiale \(r\), dal centro all'origine.
- Arco verde: angolo azimutale \(\varphi\), sul piano \(xy\).
- Arco arancione: angolo polare \(\theta\), rispetto all'asse \(z\).
- Grigio tratteggiato: proiezione del punto sul piano \(xy\).
2. Relazioni tra coordinate cartesiane e sferiche
2.1. Da coordinate sferiche a cartesiane:
2.2. Da coordinate cartesiane a sferiche:
3. Esempi dettagliati
3.1. Esempio 1: Punto sull’asse \(z\)
Supponiamo di avere un punto \(P\) di coordinate cartesiane:
\begin{equation} (x, y, z) = (0, 0, 5) \end{equation}Convertiamo in coordinate sferiche:
- \(r = \sqrt{0^2 + 0^2 + 5^2} = 5\)
- \(\theta = \arccos\left(\dfrac{5}{5}\right) = \arccos(1) = 0\)
- \(\varphi = \arctan2(0, 0)\) → convenzionalmente \(\varphi = 0\)
Coordinate sferiche: \((5, 0, 0)\)
3.2. Esempio 2: Punto sul piano \(xy\)
Punto:
\begin{equation} (x, y, z) = (3, 3, 0) \end{equation}Convertiamo:
- \(r = \sqrt{3^2 + 3^2 + 0^2} = \sqrt{18} = 3\sqrt{2}\)
- \(\theta = \arccos(0 / 3\sqrt{2}) = \arccos(0) = \pi/2\)
- \(\varphi = \arctan2(3, 3) = \pi/4\)
Coordinate sferiche: \((3\sqrt{2}, \pi/2, \pi/4)\)
3.3. Esempio 3: Conversione da coordinate sferiche a cartesiane
Dati:
\[ r = 2, \quad \theta = \frac{\pi}{3}, \quad \varphi = \frac{\pi}{6} \]
Calcolo:
- \(x = 2 \cdot \sin\left(\frac{\pi}{3}\right) \cdot \cos\left(\frac{\pi}{6}\right) = 2 \cdot \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2} = \frac{3}{2}\)
- \(y = 2 \cdot \sin\left(\frac{\pi}{3}\right) \cdot \sin\left(\frac{\pi}{6}\right) = 2 \cdot \frac{\sqrt{3}}{2} \cdot \frac{1}{2} = \frac{\sqrt{3}}{2}\)
- \(z = 2 \cdot \cos\left(\frac{\pi}{3}\right) = 2 \cdot \frac{1}{2} = 1\)
Coordinate cartesiane: \(\left(\frac{3}{2}, \frac{\sqrt{3}}{2}, 1\right)\)
4. Applicazioni delle coordinate sferiche
- Fisica (es. distribuzione di cariche, campi gravitazionali)
- Astronomia (posizione delle stelle)
- Geografia (latitudine, longitudine ≈ coordinate sferiche)
- Grafica 3D (per camera orbitale, luci, ecc.)
5. ESEMPIO :
Calcolare il volume di una sfera di raggio \(R\) usando coordinate sferiche
\[{Calcolo\ del\ volume:} \quad V = \iiint_{Sfera} dV\]
5.1. Passaggio alle coordinate sferiche
In coordinate sferiche:
- \(x = r \sin\theta \cos\varphi\)
- \(y = r \sin\theta \sin\varphi\)
- \(z = r \cos\theta\)
Il volume infinitesimo è:
\[ dV = r^2 \sin\theta \, dr \, d\theta \, d\varphi \]
Limiti di integrazione per una sfera di raggio \(R\)
- \(r \in [0, R]\)
- \(\theta \in [0, \pi]\) (da "nord" a "sud")
- \(\varphi \in [0, 2\pi]\) (intorno all'asse \(z\))
Scriviamo l'integrale triplo
\[ V = \iiint_{\text{Sfera}} dV = \int_0^{2\pi} \int_0^{\pi} \int_0^R r^2 \sin\theta \, dr \, d\theta \, d\varphi \]
Risoluzione passo-passo
- Integrale rispetto a \(r\): \[\int_0^R r^2 \, dr = \left[ \frac{r^3}{3} \right]_0^R = \frac{R^3}{3}\]
- Integrale rispetto a \(\theta\): \[\int_0^\pi \sin\theta \, d\theta = \left[ -\cos\theta \right]_0^\pi = -\cos\pi + \cos 0 = -(-1) + 1 = 2\]
- Integrale rispetto a \(\varphi\): \[\int_0^{2\pi} d\varphi = 2\pi\]
5.2. Risultato finale:
\[ V = \frac{R^3}{3} \cdot 2 \cdot 2\pi = \frac{2R^3}{3} \cdot 2\pi = \boxed{\frac{4}{3} \pi R^3} \]
6. ESEMPIO
Calcolare la massa di una sfera piena di raggio \(R\), con densità variabile radialmente
Supponiamo che la densità del materiale sia:
\[ \rho(r) = \rho_0 \left(1 - \frac{r}{R}\right) \]
dove:
- \(\rho_0\) è la densità massima al centro (\(r = 0\)),
- la densità decresce linearmente fino a \(0\) in superficie (\(r = R\)).
Formula della massa in coordinate sferiche
\[ M = \iiint_{\text{volume}} \rho(r)\, dV = \int_0^{2\pi} \int_0^{\pi} \int_0^R \rho_0 \left(1 - \frac{r}{R}\right) \cdot r^2 \sin\theta \, dr\, d\theta\, d\varphi \]
Risolviamo l'integrale
Fattori costanti fuori:
\[ M = \rho_0 \int_0^{2\pi} d\varphi \int_0^\pi \sin\theta \, d\theta \int_0^R \left(1 - \frac{r}{R}\right) r^2 \, dr \]
Integrale interno: \(r \in [0, R]\)
\[ \int_0^R \left(1 - \frac{r}{R}\right) r^2 \, dr = \int_0^R \left(r^2 - \frac{r^3}{R} \right) dr = \left[\frac{r^3}{3} - \frac{r^4}{4R}\right]_0^R = \frac{R^3}{3} - \frac{R^4}{4R} = \frac{R^3}{3} - \frac{R^3}{4} \]
\[ = R^3\left(\frac{1}{3} - \frac{1}{4}\right) = R^3 \cdot \frac{1}{12} \]
Integrale su \(\theta \in [0, \pi]\)
\[ \int_0^\pi \sin\theta\, d\theta = 2 \]
Integrale su \(\varphi \in [0, 2\pi]\)
\[ \int_0^{2\pi} d\varphi = 2\pi \]
Moltiplichiamo tutto:
\[ M = \rho_0 \cdot 2\pi \cdot 2 \cdot \frac{R^3}{12} = \rho_0 \cdot \frac{4\pi R^3}{12} = \boxed{\rho_0 \cdot \frac{\pi R^3}{3}} \]
Risultato finale:
\[ \boxed{M = \frac{\pi R^3}{3} \cdot \rho_0} \]
6.1. Interpretazione:
- Questa massa è meno di quella che si otterrebbe con densità costante \(\rho_0\) (cioè \(\frac{4}{3} \pi R^3 \cdot \rho_0\)) perché la densità decresce verso l’esterno.
- Infatti, il risultato è esattamente il 75% della massa di una sfera piena con densità costante \(\rho_0\).
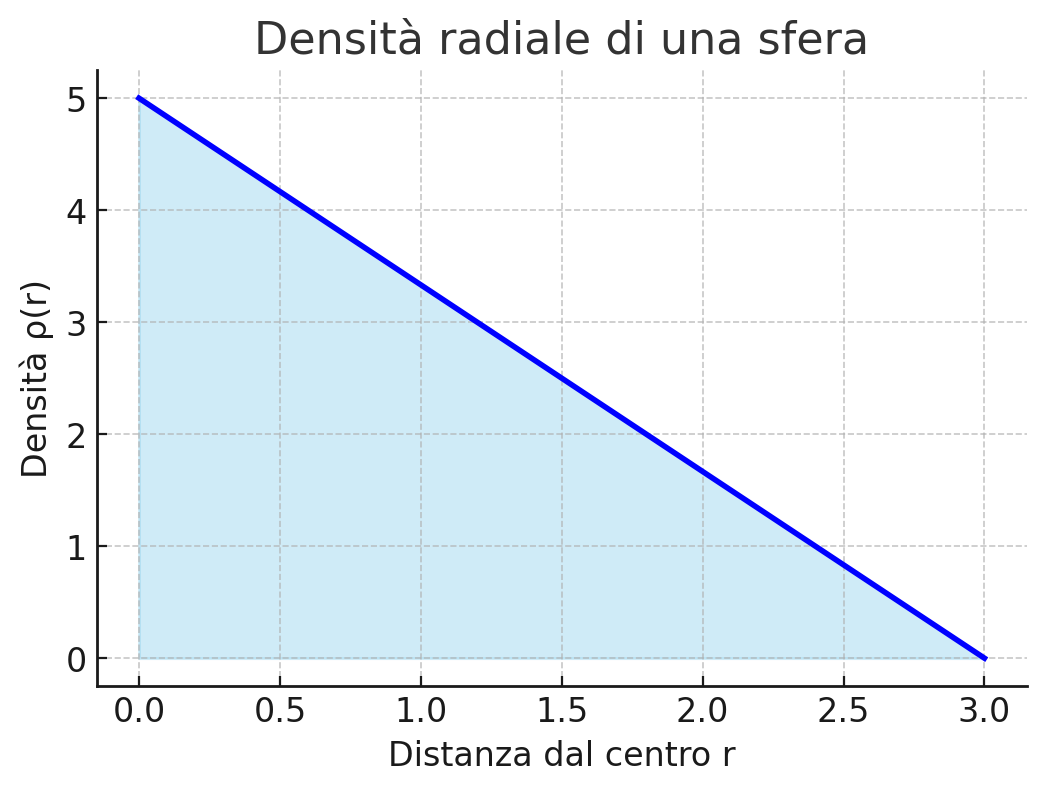
Figure 2: rappresetazione della densità
Ecco il grafico della densità radiale:
- La densità 𝜌(𝑟) parte da 𝜌(0) al centro (r=0)
- Decresce linearmente fino a 0 sulla superficie (𝑟=𝑅)
Questo rappresenta visivamente il profilo di densità usato nell’integrazione precedente