Analisi 2 - Coordinate cilindriche in \(R^3\)
Table of Contents
1. Definizione
Le coordinate cilindriche \((r,\theta,z)\) sono un sistema per rappresentare punti nello spazio \(\mathbb{R}^3\) particolarmente comodo quando il problema ha simmetria attorno all’asse \(z\). La relazione con le coordinate cartesiane \((x,y,z)\) è:
- \(x = r\cos\theta\)
- \(y = r\sin\theta\)
- \(z = z\)
con \(r\ge 0\), \(\theta\in[0,2\pi)\) (o un intervallo equivalente) e \(z\in\mathbb{R}\).
Importante: il differenziale di volume nelle coordinate cilindriche è
\[ dV = r\,dr\,d\theta\,dz, \]
dove il fattore \(r\) è il Jacobian della trasformazione (proviene dalla trasformazione \(dx\,dy = r\,dr\,d\theta\)).
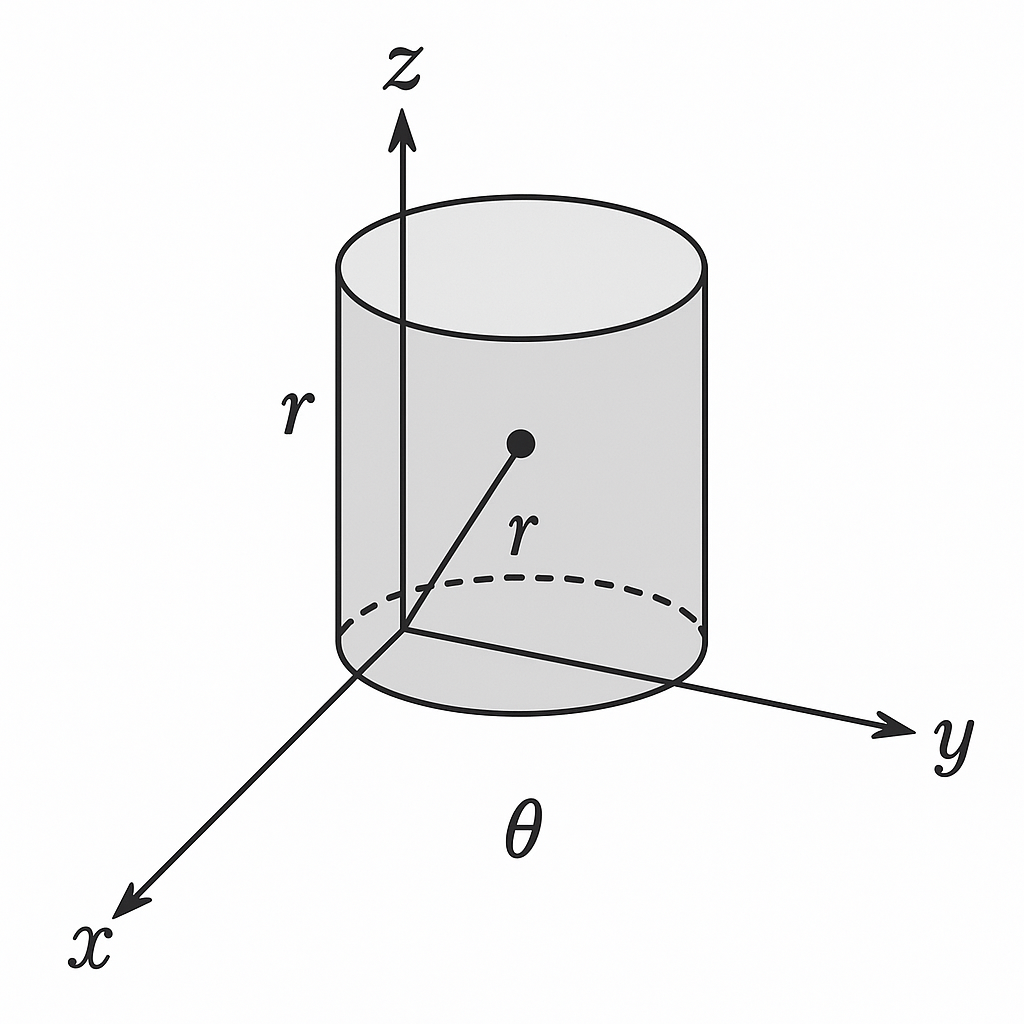
Figure 1: rappresentazione delle definizioni
Quando usare le coordinate cilindriche?
- se la regione o l’integrando ha simmetria circolare attorno all’asse \(z\) (es. cilindri, coni, tubi, ecc.);
- se l’integrando contiene \(x^2+y^2\) (diventa semplicemente \(r^2\));
- per semplificare i limiti quando le equazioni spaziali sono espresse in \(r,\theta,z\).
2. ESEMPIO
Problema. Sia \(E\) la regione nello spazio definita dal cono \(z=\sqrt{x^2+y^2}\) (cioè \(z=r\)) e dal piano \(z=2\), con \(z\ge 0\). Calcolare
\[ I=\iiint_E z\,dV. \]
Interpretazione: \(E\) è il solido formato dal cono retto con vertice nell’origine e altezza \(2\); la base ha raggio \(2\) (perché su \(z=2\) abbiamo \(r=z=2\)). Vogliamo il primo momento rispetto al piano \(xy\): integrare \(z\) su tutto il volume.
2.1. esprimere in coordinate cilindriche.
- \(z\) rimane \(z\).
- \(dV = r\,dz\,dr\,d\theta\) (ordine che preferiamo: \(dz\,dr\,d\theta\)).
2.2. limiti di integrazione.
- \(\theta\): da \(0\) a \(2\pi\) (tutta la rotazione intorno all’asse \(z\)).
- \(r\): da \(0\) fino all’intersezione con il piano \(z=2\). Poiché sulla superficie \(z=r\) e \(z=2\), allora \(r=2\). Quindi \(r\in[0,2]\).
- \(z\): per ogni \(r\) fissato, \(z\) varia dalla superficie inferiore del cono \(z=r\) fino al piano superiore \(z=2\); quindi \(z\in[r,2]\).
Quindi
\[ I=\int_{\theta=0}^{2\pi}\int_{r=0}^{2}\int_{z=r}^{2} z\,(r\,dz)\,dr\,d\theta. \]
2.3. calcolo interno (integrale in \(z\)).
Calcoliamo l’integrale interno \(\displaystyle\int_{z=r}^{2} z\,dz\):
\[ \int_{r}^{2} z\,dz=\left[\tfrac{1}{2}z^2\right]_{z=r}^{z=2}=\tfrac{1}{2}(4-r^2)=2-\tfrac{r^2}{2}. \]
Moltiplichiamo per \(r\) (dal Jacobiano):
\[ r\cdot\left(2-\tfrac{r^2}{2}\right)=2r-\tfrac{r^3}{2}. \]
2.4. integrale in \(r\).
\[ \int_{0}^{2}\left(2r-\tfrac{r^3}{2}\right)dr = \left[r^2 - \tfrac{r^4}{8}\right]_{0}^{2}. \]
Calcoliamo i termini (passo-passo per evitare errori):
- \(r^2\) valutato in \(2\) è \(2^2=4\).
- \(\tfrac{r^4}{8}\) valutato in \(2\) è \(\tfrac{2^4}{8}=\tfrac{16}{8}=2\).
Quindi l’integrale radiale vale \(4-2=2\).
2.5. integrale in \(\theta\).
\[ I=\int_{0}^{2\pi} 2\,d\theta = 2\cdot(2\pi)=4\pi. \]
2.6. Risultato finale:
$\displaystyle \iiintE z\,dV = 4π.$
Possiamo verificare il risultato usando il fatto noto che il baricentro \(z_{\text{centro}}\) di un cono retto (con apex nell’origine e base piana a \(z=h\)) è \(z_{\text{centro}}=\tfrac{3}{4}h\). Il volume del cono è \(V=\tfrac{1}{3}\pi R^2 h\). Nel nostro caso \(h=2\) e \(R=2\), quindi
\[ V=\tfrac{1}{3}\pi\cdot 2^2\cdot 2=\tfrac{8\pi}{3}, \quad z_{\text{centro}}=\tfrac{3}{4}\cdot 2=\tfrac{3}{2}. \]
Allora \(\displaystyle\iiint_E z\,dV = V\cdot z_{\text{centro}}=\tfrac{8\pi}{3}\cdot\tfrac{3}{2}=4\pi\), che coincide con il risultato trovato — buon controllo di coerenza.
3. ESEMPIO
Sia \(E\) la regione dello spazio compresa fra la sfera \(x^2+y^2+z^2=9\) (raggio \(3\)) e il cono \(z=\sqrt{x^2+y^2}\) (cioè \(z=r\)), con \(z\ge0\). Vogliamo calcolare
\[ I=\iiint_{E} z\,dV. \]
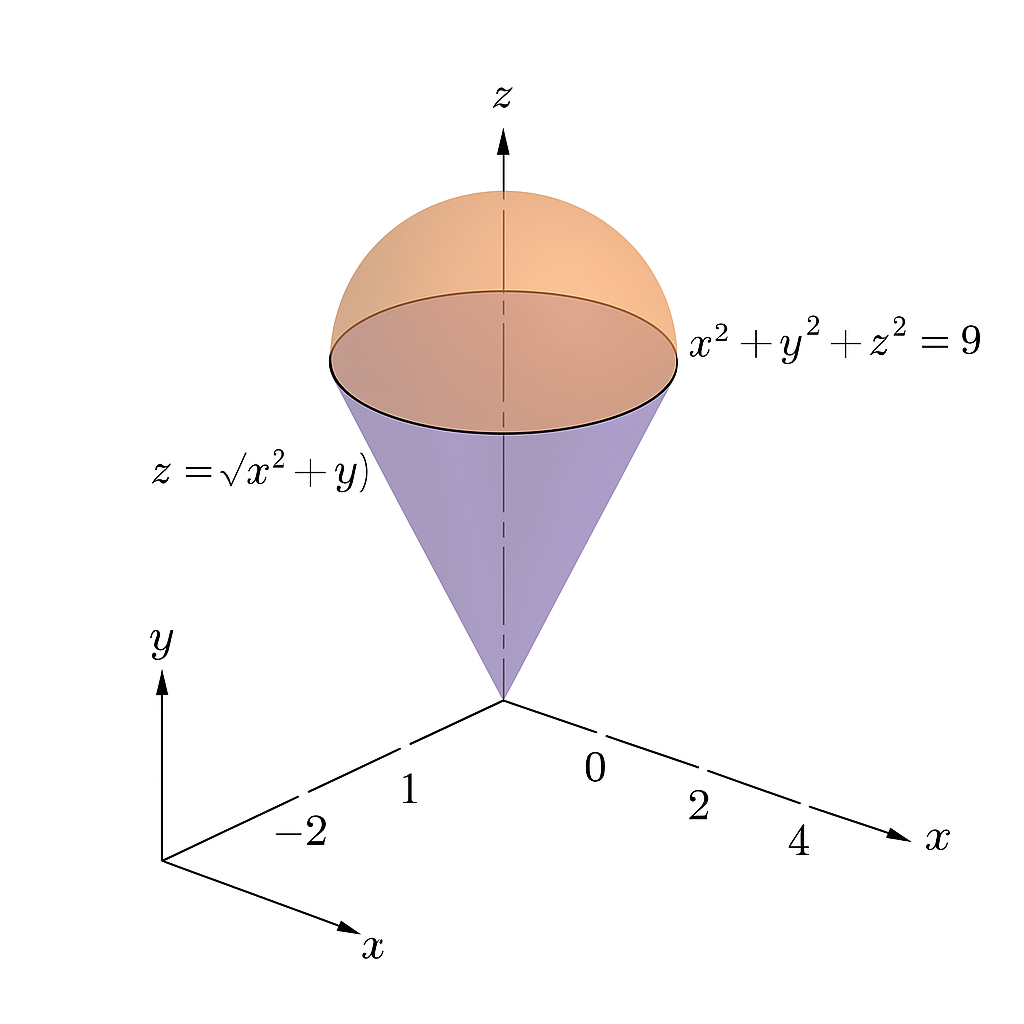
Figure 2: rappresentazione del dominio
3.1. Descrizione della regione in coordinate cilindriche
In coordinate cilindriche \((r,\theta,z)\) abbiamo:
- la sfera superiore: \(z=\sqrt{9-r^2}\),
- il cono: \(z=r\).
L’intersezione tra cono e sfera si trova risolvendo \(r=\sqrt{9-r^2}\). Elevando al quadrato:
\[ r^2 = 9 - r^2 \quad\Longrightarrow\quad 2r^2=9 \quad\Longrightarrow\quad r^2=\tfrac{9}{2}, \]
quindi
\[ r=\frac{3}{\sqrt{2}}. \]
Quindi i limiti:
- \(\theta\in[0,2\pi]\),
- \(r\in\bigl[0,\tfrac{3}{\sqrt{2}}\bigr]\),
- per ogni \(r\) fisso, \(z\in[r,\sqrt{9-r^2}]\).
Ricordando \(dV = r\,dz\,dr\,d\theta\), l’integrale diventa
\[ I=\int_{0}^{2\pi}\int_{0}^{3/\sqrt{2}}\int_{z=r}^{\sqrt{9-r^2}} z\; (r\,dz)\; dr\; d\theta. \]
3.2. Calcolo passo-passo
Integrale interno (in \(z\)):
\[ \int_{z=r}^{\sqrt{9-r^2}} z\,dz \;=\; \left[\tfrac{1}{2}z^2\right]_{r}^{\sqrt{9-r^2}} =\tfrac{1}{2}\bigl((9-r^2)-r^2\bigr) =\tfrac{1}{2}(9-2r^2) =\tfrac{9}{2}-r^2. \]
Moltiplichiamo questo risultato per il fattore \(r\) del Jacobiano:
\[ r\Big(\tfrac{9}{2}-r^2\Big)=\tfrac{9}{2}r - r^3. \]
Ora l’integrale in \(r\):
\[ \int_{0}^{3/\sqrt{2}}\Big(\tfrac{9}{2}r - r^3\Big)dr = \Big[\tfrac{9}{4}r^2 - \tfrac{1}{4}r^4\Big]_{0}^{3/\sqrt{2}}. \]
Valutiamo i termini al limite \(r=\dfrac{3}{\sqrt{2}}\).
- Primo: \(r^2=\left(\frac{3}{\sqrt{2}}\right)^2=\frac{9}{2}\)
- Secondo: \(r^4=(r^2)^2=\left(\frac{9}{2}\right)^2=\frac{81}{4}\)
Quindi
\[ \tfrac{9}{4}r^2 = \tfrac{9}{4}\cdot \tfrac{9}{2} = \tfrac{81}{8}, \qquad \tfrac{1}{4}r^4 = \tfrac{1}{4}\cdot \tfrac{81}{4} = \tfrac{81}{16}. \]
La differenza è
\[ \tfrac{81}{8} - \tfrac{81}{16} = \tfrac{162}{16}-\tfrac{81}{16} = \tfrac{81}{16}. \]
Infine l’integrale in \(\theta\):
\[ I=\int_{0}^{2\pi} \frac{81}{16}\,d\theta = \frac{81}{16}\cdot 2\pi = \frac{81\pi}{8}. \]
3.3. Risultato (esatto e approssimato)
\[ \boxed{\,\displaystyle \iiint_{E} z\,dV \;=\; \frac{81\pi}{8}\,} \]
Valore decimale approssimato:
\[ \frac{81\pi}{8}\approx 31.8086. \]
3.4. Interpretazione geometrica rapida
La regione \(E\) è il “pezzo” di sfera sopra il cono \(z=r\). L’integrando \(z\) misura il primo momento rispetto al piano \(xy\); il risultato \(\dfrac{81\pi}{8}\) è coerente (si può ricavare un controllo in coordinate sferiche se vuoi).