Analisi 2 - Curve ed integrali curvilinei in \(R^3\)
Table of Contents
1. Definizione di curva
Una curva regolare nello spazio è una funzione:
\[ \mathbf{r}: [a, b] \to \mathbb{R}^3, \quad \mathbf{r}(t) = \big(x(t), y(t), z(t)\big) \]
dove:
- \(x(t), y(t), z(t)\) sono funzioni continue e derivabili in \([a,b]\)
- il vettore derivata \(\mathbf{r}'(t) \neq \mathbf{0}\) per ogni \(t\) (no cuspidi o punti fermi)
Il parametro \(t\) “fa scorrere” un punto lungo la curva.
1.1. Tipi di rappresentazioni
- Parametrica: \(\mathbf{r}(t) = (x(t), y(t), z(t))\) (più flessibile e generale)-
Implicita: equazioni del tipo:
\[ F(x,y,z) = 0, \quad G(x,y,z) = 0 \]
(l’intersezione di due superfici è una curva)
- Esplicita: \(y = g(x)\), \(z = h(x)\) (casi semplici)
1.2. Esempi
- Retta: \(\mathbf{r}(t) = \mathbf{p} + t\mathbf{v}\)
- Cerchio nel piano \(xy\): \(\mathbf{r}(t) = (R\cos t, R\sin t, 0)\)
- Elica: \(\mathbf{r}(t) = (R\cos t, R\sin t, ct)\)
2. Lunghezza di una curva
Se \(\gamma\) è descritta da \(\mathbf{r}(t)\), la lunghezza è:
\[ L = \int_a^b \|\mathbf{r}'(t)\| \, dt \]
dove:
\[ \|\mathbf{r}'(t)\| = \sqrt{[x'(t)]^2 + [y'(t)]^2 + [z'(t)]^2} \]
2.1. Interpretazione
\(\|\mathbf{r}'(t)\|\) è la velocità istantanea del punto che percorre la curva. L’integrale somma queste velocità nel tempo → lunghezza totale.
2.2. Esempio
Per l’elica \(\mathbf{r}(t) = (\cos t, \sin t, t)\), \(t\in [0, 2\pi]\):
\[ \mathbf{r}'(t) = (-\sin t, \cos t, 1) \]
\[ \|\mathbf{r}'(t)\| = \sqrt{\sin^2 t + \cos^2 t + 1} = \sqrt{2} \]
\[ L = \int_0^{2\pi} \sqrt{2} \, dt = 2\pi \sqrt{2} \]
3. Integrali curvilinei
Esistono due tipi principali: prima specie (funzioni scalari) e seconda specie (campi vettoriali).
3.1. Integrale curvilineo di prima specie
Definizione:
\[ \int_\gamma f(x, y, z) \, ds = \int_a^b f(x(t), y(t), z(t)) \, \|\mathbf{r}'(t)\| \, dt \]
Qui \(ds\) rappresenta un infinitesimo di lunghezza.
Interpretazione: Se \(f\) è una densità lineare (massa per unità di lunghezza), questo integrale dà la massa totale di un filo con forma \(\gamma\).
3.1.1. Esempio:
Curva: semicirconferenza di raggio \(R\) nel piano \(xy\) \(\mathbf{r}(t) = (R\cos t, R\sin t, 0), \ t \in [0,\pi]\) Densità: \(f = k\) costante Risultato:
\[ \int_\gamma k\, ds = k \cdot (\text{lunghezza arco}) = k\cdot (\pi R) \]
3.2. Integrale curvilineo di seconda specie
Definizione per un campo vettoriale \(\mathbf{F}(x, y, z) = (P, Q, R)\):
\[ \int_\gamma \mathbf{F} \cdot d\mathbf{r} = \int_a^b \mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{r}'(t) \, dt \]
oppure:
\[ \int_\gamma P\,dx + Q\,dy + R\,dz \]
Qui \((dx, dy, dz) = \mathbf{r}'(t) dt\).
Interpretazione: Lavoro compiuto da un campo di forze \(\mathbf{F}\) per spostare un punto lungo \(\gamma\).
3.2.1. Esempio:
Campo \(\mathbf{F}(x, y, z) = (y, x, 0)\) Curva: arco di circonferenza \(\mathbf{r}(t) = (R\cos t, R\sin t, 0)\), \(t \in [0, \pi/2]\):
\[ \mathbf{r}'(t) = (-R\sin t, R\cos t, 0) \]
\[ \mathbf{F}(\mathbf{r}(t)) = (R\sin t, R\cos t, 0) \]
\[ \mathbf{F} \cdot \mathbf{r}'(t) = R\sin t \cdot (-R\sin t) + R\cos t \cdot (R\cos t) = -R^2\sin^2 t + R^2\cos^2 t = R^2\cos(2t) \]
\[ \int_0^{\pi/2} R^2\cos(2t) \, dt = \frac{R^2}{2} \sin(2t) \Big|_0^{\pi/2} = 0 \]
→ Lavoro nullo (forza e spostamento mediamente ortogonali).
4. Definizione \(\nabla \varphi\)
\(\nabla \varphi\) si legge “gradiente di \(\varphi\)” ed è un operatore vettoriale che, applicato a una funzione scalare \(\varphi(x,y,z)\), restituisce un campo vettoriale che indica:
- Direzione: la direzione di massima crescita di \(\varphi\)
- Verso: quello in cui \(\varphi\) aumenta
- Modulo: la velocità massima di crescita (cioè la derivata direzionale massima)
Se \(\varphi: \mathbb{R}^3 \to \mathbb{R}\) è differenziabile, allora:
\[ \nabla \varphi = \left( \frac{\partial \varphi}{\partial x}, \frac{\partial \varphi}{\partial y}, \frac{\partial \varphi}{\partial z} \right) \]
oppure, in forma compatta:
\[ \nabla \varphi = \mathbf{i} \frac{\partial \varphi}{\partial x} + \mathbf{j} \frac{\partial \varphi}{\partial y} + \mathbf{k} \frac{\partial \varphi}{\partial z} \]
dove \(\mathbf{i}, \mathbf{j}, \mathbf{k}\) sono i versori lungo \(x\), \(y\) e \(z\).
4.1. Esempio
Se:
\[ \varphi(x,y,z) = x^2 + y^2 + z^2 \]
allora:
\[ \nabla \varphi = (2x, 2y, 2z) \]
Questo è il campo vettoriale che abbiamo usato nell’esempio del teorema fondamentale degli integrali curvilinei.
5. Teorema Fondamentale dell'integrale curvilineo
Il teorema fondamentale degli integrali curvilinei in \(\mathbb{R}^3\) è, in sostanza, la versione multidimensionale del teorema fondamentale del calcolo integrale.
5.1. Enunciato
Sia \(\mathbf{F} = \nabla \varphi\) un campo vettoriale conservativo, cioè il gradiente di una funzione scalare \(\varphi(x,y,z)\) definita su un dominio aperto e connesso, e sia \(\gamma\) una curva regolare orientata da un punto \(A\) a un punto \(B\). Allora:
\[ \int_{\gamma} \mathbf{F} \cdot d\mathbf{r} = \varphi(B) - \varphi(A) \]
dove:
- \(\mathbf{F} \cdot d\mathbf{r} = P\,dx + Q\,dy + R\,dz\)
- \(\varphi\) è detta funzione potenziale del campo \(\mathbf{F}\)
5.2. Interpretazione
- L’integrale curvilineo non dipende dal percorso, ma solo dai punti iniziale e finale.
- Se \(\mathbf{F}\) è conservativo, allora \(\nabla \times \mathbf{F} = \mathbf{0}\) (rotore nullo), in domini semplicemente connessi.
5.3. Esempio
Sia:
\[ \mathbf{F}(x,y,z) = (2x, 2y, 2z) \]
Osservo che \(\mathbf{F} = \nabla \varphi\) con:
\[ \varphi(x,y,z) = x^2 + y^2 + z^2 \]
Sia \(\gamma\) una qualsiasi curva da \(A(1,0,0)\) a \(B(2,1,3)\). Allora:
\[ \int_{\gamma} \mathbf{F} \cdot d\mathbf{r} = \varphi(B) - \varphi(A) = (2^2 + 1^2 + 3^2) - (1^2 + 0^2 + 0^2) \]
\[ = (4 + 1 + 9) - 1 = 14 - 1 = 13 \]
Qualunque sia la forma di \(\gamma\), l’integrale vale 13.
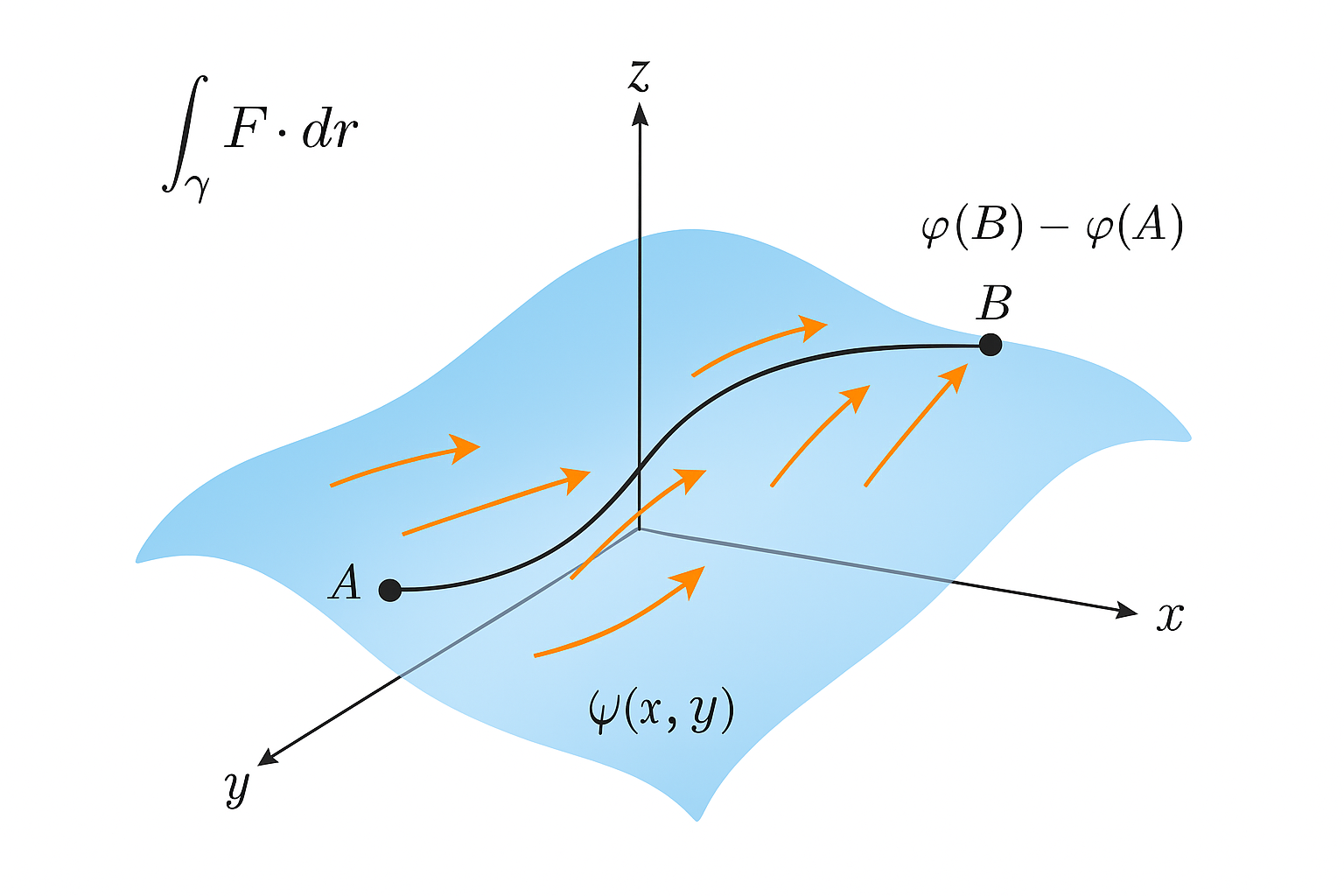
Figure 1: rappresetazione dell'esempio
5.4. Corollario
Il corollario principale del teorema fondamentale degli integrali curvilinei è:
Se un campo vettoriale \(\mathbf{F}\) è conservativo, cioè \(\mathbf{F} = \nabla \varphi\) per una funzione potenziale \(\varphi\) definita in un dominio aperto e semplicemente connesso, allora:
- Indipendenza dal cammino Per ogni coppia di punti \(A\) e \(B\) nel dominio: \[ \int_{\gamma} \mathbf{F} \cdot d\mathbf{r} \] ha lo stesso valore per qualsiasi curva \(\gamma\) che va da \(A\) a \(B\).
- Integrale lungo curve chiuse Se \(\gamma\) è una curva chiusa (cioè parte e arriva nello stesso punto): \[ \oint_{\gamma} \mathbf{F} \cdot d\mathbf{r} = 0 \] perché \(\varphi(B) - \varphi(A) = 0\) quando \(A = B\).
5.4.1. Interpretazione fisica:
Se \(\mathbf{F}\) rappresenta un campo di forze conservativo, il lavoro compiuto per muovere una particella lungo un percorso chiuso è sempre nullo: tutta l’energia fornita per andare “in salita” viene restituita “in discesa”.
6. ESEMPIO di integrale curvilineo
Circonferenza di raggio \(R>0\) nel piano \(z=0\), percorsa in verso antiorario:
\[ \mathbf r(t)=(R\cos t,\;R\sin t,\;0),\qquad t\in[0,2\pi]. \]
- Derivata: \(\mathbf r'(t)=(-R\sin t,\;R\cos t,\;0)\).
- Elemento di arco: \(\displaystyle ds=\|\mathbf r'(t)\|\,dt=R\,dt\).
6.1. Integrale curvilineo di prima specie
Calcola la “lunghezza pesata” di un filo con densità \(f(x,y,z)=x^2\).
\[ \int_{\gamma} f\,ds =\int_0^{2\pi} f(\mathbf r(t))\,\|\mathbf r'(t)\|\,dt =\int_0^{2\pi} \big(R^2\cos^2 t\big)\, R\,dt. \]
Svolgo:
\[ \int_0^{2\pi} R^3\cos^2 t\,dt =R^3\int_0^{2\pi} \frac{1+\cos(2t)}{2}\,dt =R^3\left[\frac{t}{2}+\frac{\sin(2t)}{4}\right]_0^{2\pi} =R^3\cdot\frac{2\pi}{2}=\boxed{\pi R^3}. \]
Interpretazione: massa del filo (lunghezza \(2\pi R\)) pesata dalla densità \(x^2\).
6.2. Integrale curvilineo di seconda specie
Scegliamo il campo vettoriale \(\mathbf F(x,y,z)=(-y,\;x,\;0)\). (È il campo di rotazione nel piano.)
\[ \int_{\gamma}\mathbf F\cdot d\mathbf r =\int_0^{2\pi} \mathbf F(\mathbf r(t))\cdot \mathbf r'(t)\,dt. \]
Valuto lungo la curva:
- \(\mathbf F(\mathbf r(t))=(-R\sin t,\;R\cos t,\;0)\).
- Prodotto scalare:
\[ \mathbf F(\mathbf r(t))\cdot \mathbf r'(t) =(-R\sin t)(-R\sin t)+(R\cos t)(R\cos t)=R^2(\sin^2 t+\cos^2 t)=R^2. \]
Quindi
\[ \int_{\gamma}\mathbf F\cdot d\mathbf r =\int_0^{2\pi} R^2\,dt =\boxed{2\pi R^2}. \]
Interpretazione: è la circolazione del campo attorno alla circonferenza; qui è positiva e proporzionale all’area \(\pi R^2\).
6.3. Osservazioni utili
- Nel primo caso compare \(ds\) (lunghezza): è un integrale su una funzione scalare definita sulla curva.
- Nel secondo caso compare \(d\mathbf r\): integri un campo vettoriale lungo una curva orientata.
- Se \(\mathbf F\) fosse conservativo (\(\mathbf F=\nabla\varphi\)), allora su qualsiasi curva chiusa \(\oint_\gamma \mathbf F\cdot d\mathbf r=0\).