Analisi 2 - Baricentri e Solidi di rotazione
Table of Contents
- 1. Baricentri
- 2. Introduzione ai solidi di rotazione
- 3. Volume (Guldino 2):
- 4. Area della superficie (Guldino 1): la curva generatrice è una circonferenza di lunghezza \(l=2\pi r\); il suo baricentro è a distanza \(R\):
- 5. Volume (dischi): \(V=\pi r^2 h\).
- 6. Volume (Guldino 2): area \(A=rh\), baricentro a distanza \(\rho_G=\tfrac{r}{2}\) dall’asse, quindi
- 7. Area laterale (Guldino 1):
- 8. Lunghezza arco: \(l=\pi R\).
- 9. Distanza del baricentro dell’arco semicircolare dal centro: \(\tfrac{2R}{\pi}\) (quindi stessa distanza \(\rho_C\) dal diametro-asse).
- 10. Area (Guldino 1):
- 11. Area: \(A=\tfrac{\pi R^2}{2}\).
- 12. Distanza del baricentro del semidisco dal centro: \(\tfrac{4R}{3\pi}\) (→ stessa \(\rho_G\) dal diametro).
- 13. Volume (Guldino 2):
- 14. Quando conosci (o recuperi facilmente) lunghezze/aree e baricentri delle figure generatrici.
- 15. Per solidi/superfici con simmetria (toro, cilindro, cono, sfera).
- 16. Per verifiche rapide dei risultati ottenuti con integrali.
- 17. Arco semicircolare di raggio \(R\): \(\rho_C=\dfrac{2R}{\pi}\) dal centro, sul raggio perpendicolare al diametro.
- 18. Semidisco di raggio \(R\): \(\rho_G=\dfrac{4R}{3\pi}\) dal centro, stessa direzione.
- 19. Rettangolo \(r\times h\): baricentro a \(\tfrac{r}{2}\) dalla retta mediana.
- 20. Segmento con raggi estremi \(0\) e \(r\): baricentro a \(\tfrac{r}{2}\) dall’asse.
- 21. un esercizio completo (es. toro con numeri specifici),
- 22. oppure un poster con le formule chiave (PDF stampabile),
- 23. o un grafico che mostra la costruzione dei solidi mentre ruotano.
1. Baricentri
Ecco un’illustrazione che mostra vari esempi di figure piane con i loro rispettivi centri geometrici, detti baricentri o centroidi, utili per visualizzare la teoria.

Figure 1: rappresetazione di alcuni tipi di baricentri
1.1. Cos’è il baricentro (o centroide)?
Il baricentro di una figura è il punto in cui si può idealmente considerare concentrata tutta la massa, assumendo densità uniforme. Geometricamente è la posizione media di tutti i punti della figura ([Wikipedia][1], [Wikipedia][2]).
In termini semplici:
- Se hai un triangolo, il baricentro è il punto di incontro delle sue mediane.
- Se la figura ha simmetrie, il baricentro si trova sull’asse (o sugli assi) di simmetria.
1.2. Proprietà principali
1.2.1. Triangolo
- Le mediane si incontrano tutte in un unico punto, il baricentro.
- Questa intersezione divide ogni mediana in un rapporto di 2:1, dove il tratto più lungo va dal vertice al baricentro.
In coordinate, se i vertici sono \(A(x_A,y_A)\), \(B(x_B,y_B)\), \(C(x_C,y_C)\), il baricentro \(G\) ha:
\[ G\left(\frac{x_A+x_B+x_C}{3},\;\frac{y_A+y_B+y_C}{3}\right) \] :contentReference[oaicite:5]{index=5}. \]
1.2.2. Figura piana generica
Il baricentro è la media ponderata delle posizioni di tutti i punti della figura. Se la figura ha densità uniforme, coincide con il centro di massa.
1.2.3. Baricentro come posizione di equilibrio
Se sospendi la figura dal baricentro, essa rimane in equilibrio (come se fosse perfettamente bilanciata).
1.2.4. Formula generale (area continua)
Per una regione piana \(A\):
\[ \bar x = \frac{1}{A} \iint_A x\,dA, \quad \bar y = \frac{1}{A} \iint_A y\,dA \]
Questo calcolo richiede di integrare le coordinate nel dominio della figura.
1.2.5. Distribuzione di punti discreti
Per \(k\) punti \(\mathbf{x}_1, \dots, \mathbf{x}_k\), il baricentro è:
\[ \mathbf{X}_G = \frac{\mathbf{x}_1 + \cdots + \mathbf{x}_k}{k} \]
una semplice media aritmetica ([Wikipedia][2]).
1.2.6. Proprietà vari
- Il baricentro di una figura concava può trovarsi anche al di fuori della figura, come nel caso di una falce di luna.
- È anche usato come centro di pressione nella fluidodinamica, indicando dove può essere applicata la forza risultante.
1.3. Esempi pratici
1.3.1. Baricentro di un triangolo
Triangolo con vertici \((0,0)\), \((a,0)\), \((0,b)\). Coordinate del baricentro:
\[ \left(\frac{0 + a + 0}{3}, \frac{0 + 0 + b}{3}\right) = \left(\frac{a}{3},\,\frac{b}{3}\right). \]
1.3.2. Regione piana generica
Se \(A\) è la regione sotto la curva \(y=f(x)\) tra \(x=a\) e \(x=b\):
- \(\displaystyle \bar x = \frac{1}{A} \int_a^b x [f(x)]\,dx\),
- \(\displaystyle \bar y = \frac{1}{A} \int_a^b \frac{1}{2}[f(x)]^2\,dx\), dove \(A = \int_a^b f(x)\,dx\) è l’area.
1.3.3. Figura composta
Se un’area è la somma di sottoregioni più semplici, puoi calcolare il baricentro sommando i contributi delle sottoregioni, ponderati per le loro aree (o lunghezze, se si tratta di curve).
2. Introduzione ai solidi di rotazione
Un solido di rotazione si ottiene ruotando una figura piana (una regione o una curva) intorno a un asse contenuto nel suo piano e non intersecante la figura stessa.
- Ad esempio, ruotando un rettangolo su un suo lato otteniamo un cilindro.
- Ruotando un triangolo rettangolo otteniamo un cono.
- Ruotando una semicirconferenza intorno al suo diametro si genera una sfera ([Treccani][1], [Wikipedia][2]).
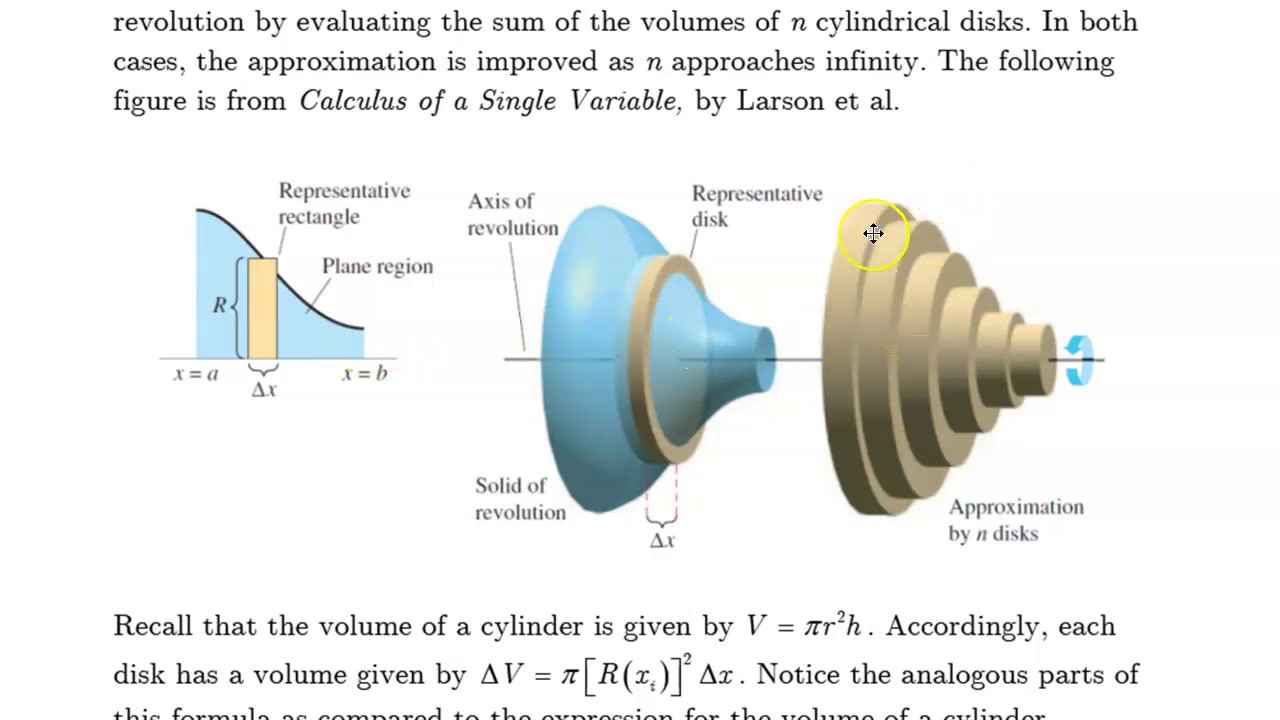
Figure 2: rappresetazione di un solido di rotazione
2.1. Metodi classici per il calcolo di area e volume
Metodo dei dischi Si considera la rotazione di una funzione \(y = f(x)\) attorno all’asse \(x\). Un piccolo elemento ha forma di disco di raggio \(f(x)\), quindi:
\[ \text{Volume} = \int_a^b \pi [f(x)]^2 \, dx. \]
Metodo dei “washers” (anelli) Se la regione è compresa tra due curve \(f(x)\) e \(g(x)\), si ruota attorno all’asse \(x\):
\[ V =\int_a^b\pi\big(R_{\text{est}}(x)^2-R_{\text{int}}(x)^2\big)\,dx = \int_a^b \pi \big([f(x)]^2 - [g(x)]^2\big)\, dx. \]
Gusci cilindrici (shells), rotazione attorno all’asse \(y\):
\[ V=\int_a^b 2\pi\,(\text{raggio})\cdot(\text{altezza})\,dx. \]
Area di superficie di rivoluzione per \(y=f(x)\) attorno a \(x\):
\[ S=2\pi\int_a^b f(x)\,\sqrt{1+[f'(x)]^2}\,dx. \]
2.2. I teoremi di Guldino
Ci sono due teoremi fondamentali, molto utili e spesso più semplici da applicare, specialmente quando si conoscono le proprietà geometriche (area, lunghezza, baricentro):
Quando convengono i teoremi di Guldino:
- Quando conosci (o recuperi facilmente) lunghezze/aree e baricentri delle figure generatrici.
- Per solidi/superfici con simmetria (toro, cilindro, cono, sfera).
- Per verifiche rapide dei risultati ottenuti con integrali.
2.2.1. Primo teorema – Area della superficie di rotazione
Se ruotiamo una curva piana \(\gamma\), di lunghezza \(l\), attorno a un asse complanare ed esterno alla curva, allora l’*area* della superficie di rivoluzione è:
\[ A = l \cdot d, \]
dove \(d\) è la distanza percorsa dal baricentro della curva durante la rotazione (circumferenza di raggio \(d\)).
2.2.2. Secondo teorema – Volume del solido di rotazione
Se ruotiamo una figura piana \(K\) (con area \(A\)) attorno a un asse complanare ed esterno, il volume generato è:
\[ V = A \cdot d, \]
dove \(d\) è la lunghezza della traiettoria del baricentro di \(K\) (tipicamente una circonferenza).
2.3. Esempi concreti
2.3.1. Volume di un toro (ciambella)
- Regione \(K\): cerchio di raggio \(r\), area \(A = \pi r^2\).
- Asse: distante \(R\) dal centro del cerchio, con \(R > r\).
- Baricentro del cerchio descrive una circonferenza di lunghezza \(d = 2\pi R\).
Applicando Guldino:
\[ V = A \cdot d = \pi r^2 \cdot 2\pi R = 2\pi^2 r^2 R. \]
È proprio la formula del volume di un toro.
2.3.2. Volume di un cilindro (rettangolo)
- Regione \(K\): rettangolo di base \(r\) e altezza \(h\), area \(A = r \cdot h\).
- Asse: lungo il lato di altezza \(h\). Il baricentro del rettangolo, posto a distanza \(\tfrac{r}{2}\) dall'asse, percorre \(d = 2\pi\cdot \frac{r}{2} = \pi r\).
Volume:
\[ V = A \cdot d = (r h)\cdot (\pi r) = \pi r^2 h, \]
ossia il volume standard del cilindro.
2.4. Riepilogo dei concetti
| Concetto | Formula con Guldino | Quando usarla |
|---|---|---|
| Area superficie di rotazione | \(A = l \cdot d\) | Conosci lunghezza dell’arco e baricentro |
| Volume solido di rotazione | \(V = A \cdot d\) | Conosci area della regione e baricentro |
Condizioni d’uso: valenza solo se la figura o curva ruotano attorno a un asse complanare ma esterno (non interseca la figura) e in un dominio semplice o circolare.
—
Primo teorema (superficie) Se una curva piana di lunghezza \(l\) ruota attorno a un asse esterno alla curva, l’area della superficie di rivoluzione è
\[ S = l \cdot (2\pi\,\rho_C), \]
dove \(\rho_C\) è la distanza del baricentro della curva dall’asse.
Secondo teorema (volume) Se una regione piana di area \(A\) ruota attorno a un asse esterno alla regione, il volume generato è
\[ V = A \cdot (2\pi\,\rho_G), \]
dove \(\rho_G\) è la distanza del baricentro dell’area dall’asse.
> Condizioni tipiche: asse nel piano della figura/curva e non secante la figura (o comunque baricentro con traiettoria circolare ben definita).
—
## A) Toro (ciambella) — Guldino vs. integrali
Generatrice: cerchio di raggio \(r\) (area \(A=\pi r^2\)), centro a distanza \(R>r\) dall’asse di rotazione.
3. Volume (Guldino 2):
\[ V = A\cdot(2\pi R)=\pi r^2 \cdot 2\pi R=\boxed{2\pi^2 R r^2}. \]
4. Area della superficie (Guldino 1): la curva generatrice è una circonferenza di lunghezza \(l=2\pi r\); il suo baricentro è a distanza \(R\):
\[ S = l\cdot(2\pi R)=2\pi r\cdot 2\pi R=\boxed{4\pi^2 R r}. \]
(Controllo con integrali: possibile ma più laborioso; i risultati coincidono.)
—
## B) Cilindro retto — metodo classico e Guldino
Generatrice di volume: rettangolo \(r\times h\) che ruota attorno al lato \(h\).
5. Volume (dischi): \(V=\pi r^2 h\).
6. Volume (Guldino 2): area \(A=rh\), baricentro a distanza \(\rho_G=\tfrac{r}{2}\) dall’asse, quindi
\[ V=A\cdot(2\pi\rho_G)=rh\cdot(2\pi\cdot \tfrac{r}{2})=\boxed{\pi r^2 h}. \]
Superficie laterale: generatrice curva = segmento di lunghezza \(h\) a distanza costante \(r\) dall’asse.
7. Area laterale (Guldino 1):
\[ S_{\text{lat}}=h\cdot(2\pi r)=\boxed{2\pi r h}. \]
—
## C) Cono retto (raggio \(r\), altezza \(h\), apice sull’asse)
Volume (dischi):
\[ V=\int_0^h \pi\left(\frac{r}{h}z\right)^2\,dz=\pi\frac{r^2}{h^2}\cdot \frac{h^3}{3}=\boxed{\frac{\pi r^2 h}{3}}. \]
Superficie laterale (Guldino 1): generatrice = segmento di lunghezza \(s=\sqrt{r^2+h^2}\) (apotema), i cui punti hanno distanza dall’asse che varia linearmente da \(0\) a \(r\). Il baricentro della curva è il punto medio del segmento → distanza media \(\rho_C=\tfrac{r}{2}\). Quindi:
\[ S_{\text{lat}} = s \cdot (2\pi \rho_C)= s\cdot (2\pi \tfrac{r}{2})=\boxed{\pi r s}. \]
—
## D) Sfera di raggio \(R\) — solo Guldino (e confronto)
Superficie: ruota la semicirconferenza (arco) di raggio \(R\) attorno al diametro.
8. Lunghezza arco: \(l=\pi R\).
9. Distanza del baricentro dell’arco semicircolare dal centro: \(\tfrac{2R}{\pi}\) (quindi stessa distanza \(\rho_C\) dal diametro-asse).
10. Area (Guldino 1):
\[ S = l\cdot(2\pi \rho_C)=\pi R \cdot 2\pi \cdot \frac{2R}{\pi}=\boxed{4\pi R^2}. \]
Volume: ruota la semidisco (area) di raggio \(R\) attorno al diametro.
11. Area: \(A=\tfrac{\pi R^2}{2}\).
12. Distanza del baricentro del semidisco dal centro: \(\tfrac{4R}{3\pi}\) (→ stessa \(\rho_G\) dal diametro).
13. Volume (Guldino 2):
\[ V = A\cdot(2\pi \rho_G)=\frac{\pi R^2}{2}\cdot 2\pi\cdot \frac{4R}{3\pi} =\boxed{\frac{4}{3}\pi R^3}. \]
(Controllo col metodo dei dischi: stessi valori.)
—
14. Quando conosci (o recuperi facilmente) lunghezze/aree e baricentri delle figure generatrici.
15. Per solidi/superfici con simmetria (toro, cilindro, cono, sfera).
16. Per verifiche rapide dei risultati ottenuti con integrali.
—
17. Arco semicircolare di raggio \(R\): \(\rho_C=\dfrac{2R}{\pi}\) dal centro, sul raggio perpendicolare al diametro.
18. Semidisco di raggio \(R\): \(\rho_G=\dfrac{4R}{3\pi}\) dal centro, stessa direzione.
19. Rettangolo \(r\times h\): baricentro a \(\tfrac{r}{2}\) dalla retta mediana.
20. Segmento con raggi estremi \(0\) e \(r\): baricentro a \(\tfrac{r}{2}\) dall’asse.
—
Se vuoi, ti preparo: