Inviluppo Complesso
Table of Contents
1. Teorema dell'inviluppo
1.1. Premessa
Sia \(x(t)\) un segnale reale modulato ( parte blu fig 4 ) tramite un segnale modulante ( $~{x}(t)=A(t)ejφ(t) ) in ampiezza/fase/frequenza ( parte rossa - fig 4 ) e sia \(X(F)\) lo spettro del segnale modulato ( vds fig 2 ) il quale essendo un segnale complesso ha due parti speculari, una a frequenze negative \(X^-(F)\) ed una a frequenze positive \(X^+(F)\) detta segnale analitico come indicato nella \eqref{eq:101010} ed entrambe contengono la stessa informazione ( vds nota 1).
Per ottenere l'informazione utile e' possibile utilizzare il segnale dell'inviluppo complesso \(\tilde{X}(F)\) ( traslazione del segnale analitico in banda base - vds fig 3 noto anche come segnale in banda base ) rappresentato dalla \eqref{eq:1010} e dalla quale possiamo ricavare \(X^+(F)\) come indicato nella \eqref{eq:1919} la quale antitrasformata diventa la \eqref{eq:10101}.
\begin{equation} \label{eq:101010} X(F)=X^+(F) + jX^-(F) \end{equation} \begin{equation} \label{eq:1010} \begin{split} \tilde{X}(F)=X^+(F)(f + f_0) \end{split} \end{equation} \begin{equation} \label{eq:1919} \begin{split} X^+(F)=\tilde{X}(F)(f - f_0) \end{split} \end{equation} \begin{equation} \label{eq:10101} \begin{split} x^+(t)=\tilde{x}(t)e^{j 2\pi f_0 t}=A(t)e^{j\phi(t)}e^{j2\pi f_0 t} \end{split} \end{equation}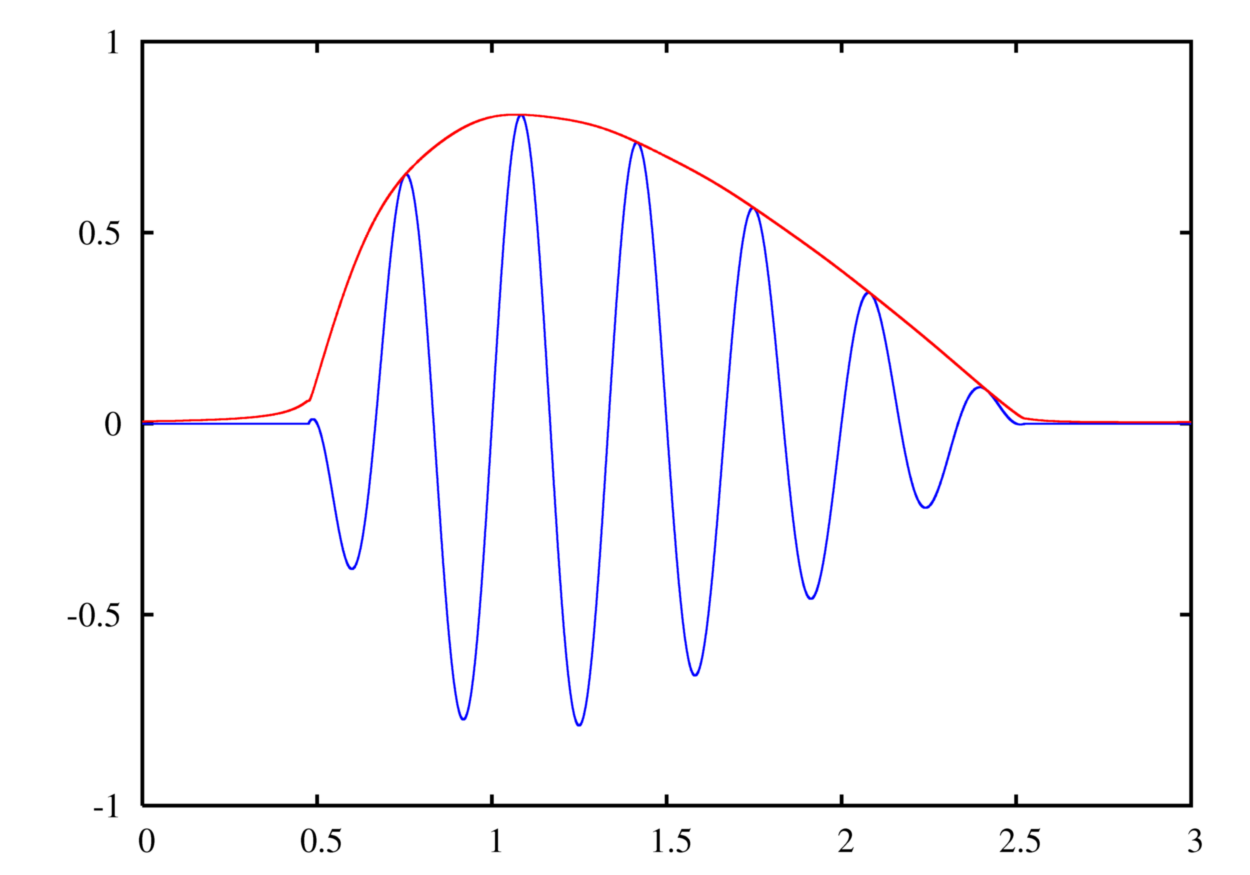
Figure 1: Esempio si segnale reale \(x(t)\)
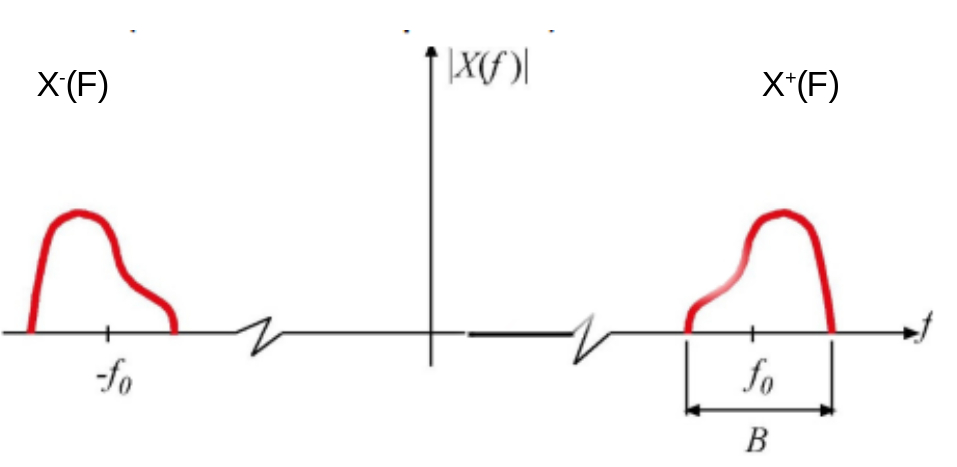
Figure 2: Spettro del segnale
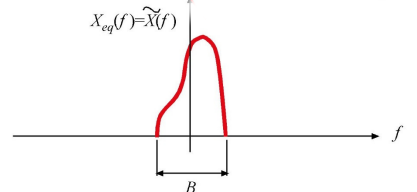
Figure 3: Segnale in banda base
1.2. Componenti del segnale
La \(X^+(F)\) della \eqref{eq:1010} puo' essere ottenuta come nella \eqref{eq:1020} in cui il fattore 2 è introdotto in quanto occorre mantenere la stessa energia del segnale completo.
Nella \eqref{eq:103001} è definito il gradino unitario la cui antitrasformata, per la proprieta' della dualita' della TDF, è quella riportata nella \eqref{eq:103002} ( vds tdf della funzione \(sgn[t]\) della teoria della delta di Dirac )
\begin{equation} \label{eq:1020} \begin{split} X^+(F)=X(F)2U(F) \end{split} \end{equation} \begin{equation} \label{eq:103001} \begin{split} U[F] =\frac{1}{2}[sgn[F] + 1] \end{split} \end{equation} \begin{equation} \label{eq:103002} \begin{split} u(t) = \frac{1}{2}[\frac{1}{j\pi (- t)} + \delta(-t)] =\frac{1}{2}[\frac{j}{\pi t} + \delta(t)] \end{split} \end{equation}Antitrasformando la \eqref{eq:1020} otteniamo la \eqref{eq:10301} in cui \(\hat{x}(t)\) e' la TDH di \(x(t)\). Il tutto puo' essere riepilogato nella \eqref{eq:10302} da cui si vede che il segnale analitico è composto da una parte reale ed una immaginaria.
\begin{equation} \label{eq:10301} \begin{split} x^+(t)=(x(t) \otimes 2u(t))= \\ (x(t) \otimes \frac{j}{\pi t}) + (x(t) \otimes \delta(t)) = \\ (x(t) \otimes \frac{j}{\pi t}) + x(t) = j\hat{x}(t) + x(t) \end{split} \end{equation} \begin{equation} \label{eq:10302} \begin{split} x^+(t)= x(t) + j\hat{x}(t) \end{split} \end{equation}Inserendo nella \eqref{eq:10302} la \eqref{eq:10101} si ricava la \eqref{eq:1111} dalla quale si evince che il segnale dell'inviluppo complesso2 e' composto da una parte immaginaria ed una reale ( vds \eqref{eq:01111} ) la quale come indicato nella \eqref{eq:0104} e' formata dalle seguenti componenti
- \(cos(2\pi f_0 t)\) = portante in fase
- \(sin(2\pi f_0 t)\) = portante in quadratura
- \(x_I(t) = A(t) cos \phi(t) = Re[x(t)]\) = componente in fase di \(x(t)\)
- \(x_Q (t) = A(t) sin \phi(t) = Im[x(t)]\) = componente in quadratura di \(x(t)\)
- Inviluppo \(A(t)=\sqrt{x^2 + \hat{x}^2}\)
- Fase \(\phi(t)=arg(x^+(t) + j\hat{x}(t))\)
Per ottenere le varie modulazioni si varia una delle parti della \eqref{eq:1111} mentre le altre rimangono costanti :
- \(A(t)\) modulazione in ampiezza;
- \(e^{j 2\pi f_0 t}\) modulazione in frequenza;
- \(e^{\phi(t)}\) modulazione di fase.
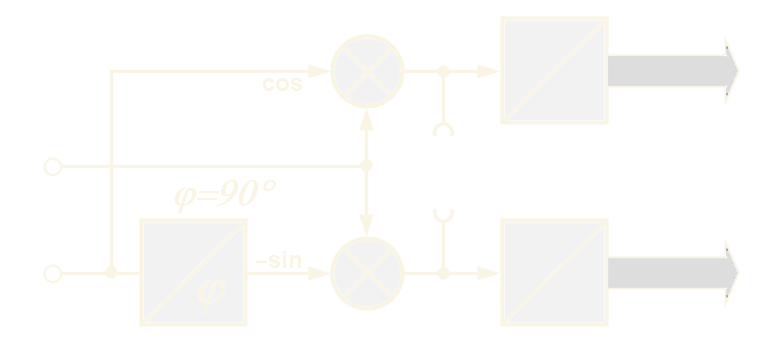
Figure 4: Implementazione della \eqref{eq:0104}
1.3. Implementazione - Filtro di Hilbert
Per prima cosa si verifica la \eqref{eq:1020} effettuando la TDF della \eqref{eq:10302} ottenedo la \eqref{eq:103} dalla quale si evince che l'uguaglianza di cui \eqref{eq:1020} e' corretta ed inoltre si evince che la funzione di trasferimento \(H(F)\) del filtro e' la TDF di \(h(t)=\frac{1}{\pi t}\).
\begin{equation} \label{eq:103} \begin{split} X^+(f)=\mathcal{F}[x^+(t)]=X(f) + j\mathcal{F}[\hat{X}(t)] = \\ X(f) + j[X(f)(-jsgn(f))]= \\ = X(f) + X(f)sgn(f) = \\ = X(f)[1+ sgn(f)] = \begin{cases} 2X(f) & f>0 \\ X(f) & f=0\\ 0 & f<0 \end{cases} \\ \simeq 2X(f)[1 + sgn(f)]=X(f)2U(f)=X(f)H(f) \end{split} \end{equation}