Serie di Fourier
Table of Contents
1. Premessa
- In uno spazio metrico è possibile definire il concetto di distanza su cui si basa la definizione di limite di modo da mantenere inalterata la teoria dell'analisi;
- Tutti i segnali misurabili in energia/potenza rappresentano uno spazio metrico in cui ogni segnale può essere rappresentato come un vettore;
- La distanza in uno spazio metrico vettoriale è definita come la norma della differenza : \(||\vec{g} -\vec{w}||\);
- La definizione di norma si basa sulla definizione di prodotto interno ;
- Il prodotto interno1 è quell'operazione t.c. se applicata a due vettori rende possibile associare uno scalare2 anche nullo ( vettori ortogonali ) appartenente allo stesso campo sul quale sono definiti i vettori.
Gli spazi con le caratteristiche di cui sopra sono quelli di Hilbert.
1.1. Prodotto Interno o scalare
In uno spazio vettoriale, un prodotto interno è una funzione che associa a ciascuna coppia di vettori un numero appartenete allo stesso campo delle componenti dei vettori. In pratica se le componenti sono reali il prodotto interno e' un numero reale. Questa funzione soddisfa alcune proprietà, come la linearità e la simmetria. Nel caso di un vettore coincide anche con il quadrato della norma.
A livello geometrico rappresenta la proiezione
\begin{equation} \label{orgfb8b4ff} <\vec g,\vec w >=\int \lvert g(t) w^c(t) \rvert d_{t} \end{equation}da notare che nella precedente definizione l'argomento dell'integrale e' una somma di monomi e nel caso di vettori finiti si ha3 :
\begin{equation} \langle g,w\rangle= \sum_{i=1}^{n} g_i w^T_i \end{equation}in cui l'argomento della sommatoria vale
\begin{equation} \begin{bmatrix} g_{1} & \cdots & g_{n}\\ \end{bmatrix} \begin{bmatrix} w_{1} \\ \vdots \\ w_{n} \\ \end{bmatrix} \end{equation}1.2. Norma
E' la radice quadrata del prodotto interno applicato ad uno stesso vettore. E' uno scalare è reale
\begin{equation}\begin{split} \label{org0e7818d} ||\vec{v}||=\sqrt{u_1^2 + ... + u_n^2} \end{split}\end{equation} \begin{equation} \label{org6f8dcc9} \lVert \vec g \rVert = (<\vec g,\vec g >)^{1/2}=(\int \lvert g(t)g^c(t) \rvert d_{t})^{1/2} \end{equation}- Positività: ∣∣w∣∣ ≥ 0 , e ∣∣w∣∣=0 sse w=0;
- Omogeneità: ∣∣α w∣∣ =∣∣α∣∣∣∣w∣∣ per ogni scalare α;
- Disuguaglianza triangolare: ∣∣v+w∣∣≤∣∣v∣∣+∣∣w∣∣ (disuguaglianza di Cauchy-Schwarz).
1.3. Distanza tra vettori
Questa misura rappresenta la distanza percorsa lungo gli assi ortogonali per raggiungere il punto di destinazione.
\begin{equation} \label{orgfceaad7} d(\vec g, \vec w )=||\vec{g}-\vec{w}||=||\vec{k}||=(\int_{a}^{b} |k(t)k^c(t)| d_{t})^{1/2} \end{equation}in cui l'intervallo \([a,b]\) è quello di definizione dei segnali e può essere illimitato. Distanza e norma possono essere messe in relazione tramite :
\begin{equation} \label{org3ca306d} d(\vec g, 0)= (\int \lvert g(t) - 0) \rvert d_{t})^{1/2}=(\int (\lvert g(t)g^c(t) \rvert)^2 d_{t})^{1/2}=\lvert <\vec g, \vec g> \rvert^{1/2}=\lVert \vec g \rVert \end{equation}la norma di un vettore è la sua distanza dall'origine.
1.4. Versori
Vettori con norma unitaria definiti come nella \eqref{orgcc8ff78}. Il versore mantiene la stessa direzione del vettore originale, questo rende i versori utili in situazioni in cui è importante descrivere solo la direzione di un vettore senza preoccuparsi della sua magnitudine.
Ad esempio, se hai un vettore velocità \(\vec g\) che rappresenta il movimento di un oggetto e vuoi descrivere solo la direzione del movimento indipendentemente dalla velocità effettiva, puoi utilizzare il versore
\begin{equation} \label{orgcc8ff78} \vec \phi = \frac{\vec g}{\lVert \vec g \rVert} \end{equation}1.5. Disuguaglianza di Swartz
L'ineguaglianza di Schwartz impone un limite superiore al prodotto scalare che e' massimo quando i due vettori sono allineati.
\begin{equation} \label{eq:1101 } \begin{split} |<\vec{g}, \vec{w}>| \leq ||g|| \; ||w|| \end{split} \end{equation} \begin{equation}\begin{split} \label{orgfadf81b} <\vec g, \vec w> \leq \lvert <\vec g, \vec w> \rvert \leq \lvert <\vec g, \vec w> \rvert^2 \\ = \int \lvert g(t)w^c(t) \rvert^2 d_{t}= \\ \int \lvert g(t)\rvert^2 \lvert w^c(t) \rvert^2 d_{t} \leq \int \lvert g(t)\rvert^2 d_{t} \int \lvert w^c(t) \rvert^2 d_{t} = \\ \lVert \vec g \rVert^2 \lVert \vec w \rVert^2 \end{split}\end{equation}da cui
\begin{equation} \label{orge73b26b} <\vec g, \vec w> \leq \lVert \vec g \rVert^2 \lVert \vec w \rVert^2 \end{equation}Dalla \eqref{orge73b26b} si ha
\begin{equation} \label{org431429b} \frac{<\vec g, \vec w>}{\lVert \vec g \rVert^2 \lVert \vec w \rVert^2} \leq 1 \end{equation} \begin{equation} \label{orgc0c7138} \frac{|<\vec g, \vec w>|}{|\lVert \vec g \rVert^2 \lVert \vec w \rVert^2|} \leq 1 \end{equation} \begin{equation} \label{eq:sw} \frac{|<\vec g, \vec w>|}{\lVert \vec g \rVert \lVert \vec w \rVert} = \cos(\theta) \leq 1 \end{equation}che vale 1 solo se i vettori sono lineramenti indipendenti ( vds \eqref{eq:155} ) cioe' l'angolo tra vettori e' \(0\) linearmente dipendenti, mentre vale 0 se l'angolo tra vettori e' \(\frac{\pi}{2}\). In pratica la disuguaglianza indica se due vettori sono linearmente indipendenti \(=0\) oppure se sono dipendenti \(\neq 0\).
1.5.1. Dimostrazione della definizione dell'angolo tra vettori
Questa parte dimostra come il prodotto interno sia legato all'angolo tra vettori come espresso nella \eqref{eq:sw1}
\begin{equation} \label{eq:sw1} {|<\vec g, \vec w>|} \leq cos(\theta){\lVert \vec g \rVert \lVert \vec w \rVert} \end{equation}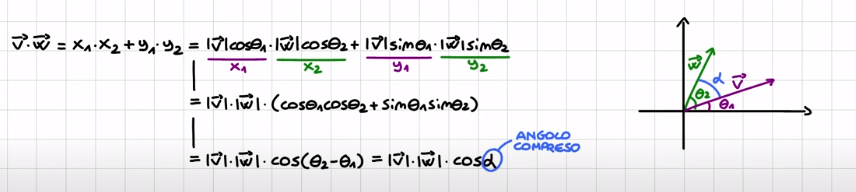
Figure 1: Angolo tra vettori
Nel caso di vettori complessi
\begin{equation} \label{eq:15} cos(\theta)= \frac{Re(<\vec v,\vec w>)}{\lVert \vec v \rVert \lVert \vec w \rVert} \end{equation}da cui
\begin{equation} \label{eq:155} Re(<\vec v,\vec w>)=|<\vec v,\vec w>|=cos(\theta){\lVert \vec v \rVert \lVert \vec w \rVert} \end{equation}dove nella \eqref{eq:155} si evince la relazione tra disuguaglianza di Swartz e angolo tra vettori.
1.6. Vettori Ortonormali
Versori a due a due perpendicolari cioe' versori a due a due in cui la loro disuguaglianza di S. e' nulla.
2. Coeficente della SDF
Scopo di questa parte di teoria e' dimostrare che il coeficente della SDF di segnali visti come vettori e' la sommatoria delle proiezioni del segnale originale.
2.1. Proiezione di un vettore lungo un altro
In riferimento alla fig 2 si ha la \eqref{eq:00}
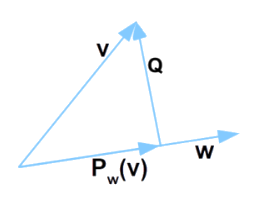
Figure 2: Proiezione di v su w
ma
\begin{equation} \label{eq:8 } <\vec{Q} \times \vec{w}> = 0 \end{equation}perche' Q ⊥ w per cui
\begin{equation} \label{eq:9 } <\vec{v} \times \vec{w}>= <\lambda \vec{w} \times \vec{w}>= \lambda< \vec{w} \times \vec{w}> \end{equation} \begin{equation} \label{eq:10} \lambda = \frac{<\vec{v} \times \vec{w}>}{||w||^2}=\frac{<\vec{v} \times \vec{w}>}{||w||||w||} \end{equation} \begin{equation} \label{dim1} \vec{P_w}=\lambda \vec{w} \end{equation} \begin{equation} \label{eq:11 } \vec{P_w}=\frac{<\vec{v} \times \vec{w}>}{||w||||w||}=\vec{w}=<\vec{v},vers(w)>vers(w) \end{equation}inoltre dalla \eqref{eq:15} si ottiene l'espressione geometrica del prodotto scalare :
\begin{equation} \label{eq:16} cos(\theta)(|| \vec v ||\; || \vec w ||)= <\vec v,\vec w> \end{equation} \begin{equation} \label{eq:010} \begin{split} \vec{P_w} = < \vec{v} \times \frac{\vec{w}}{||w||} >\frac{\vec{w}}{||w||}= < \vec{v} \times vers(w)> vers(w)= \\ cos(\theta)\vec{v}vers(w) \end{split} \end{equation}\(\vec{P_w}\) puo' essere visto come l'iesimo elemento della SDF mentre \(cos(\theta)\vec{v}\) puo' essere visto come il coeficente della SDF mentre il versore w come un armonica. Questo dimostra inoltre come una genrica armonica contribuisce alla ricostruzione del segnale.
2.2. Definizione del coeficente della SDF
Cosi come la \eqref{eq:19} rappresenta il vettore \(\vec{V}\) ( vds fig. 3 ) la SDF rappresenta il segnale \(g\) all'instante \(t\) ( vds fig. 4 ). L'argomento della SDF e' la somma degli \(n\) segnali sinusoidali \(e^{j2\pi\frac{n}{T}t}\) ognuno dei quali di ampiezza \(G_n\). Nel caso si usino i vettori per rappresentare i segnali allora la SDF puo' essere interpretata come la somma delle norme dei vettori \(G_ne^{j2\pi\frac{n}{T}t}\).
In entrambi, quello del vettore e quello della SDF, l'argomento e' il prodotto di due parti in cui il primo e' un coeficente ottenibile mediante prodotto interno e il secondo e' un versore :
- per il vettore : \(v_i=<\vec{v}, \textit{w}>\) \(i-esima\) proiezione di \(V\) lungo il versore \(w_i\)
- per la SDF : il coeficente moltiplicativo \(G_n\) ( vds \eqref{eq:gn} ) per l' \(n-esima\) sinusoide;
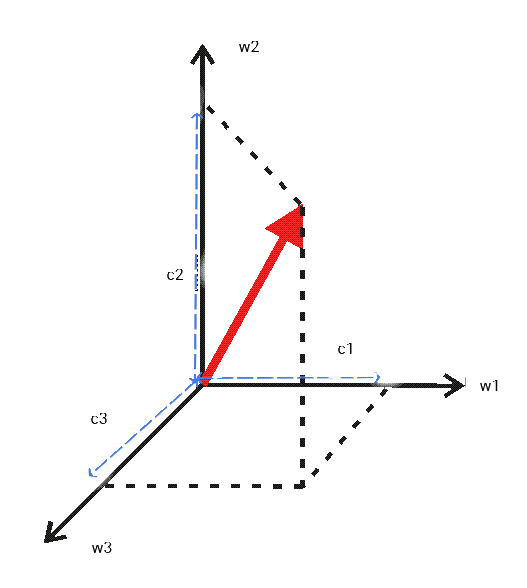
Figure 3: rappresetazione delle componenti di un vettore
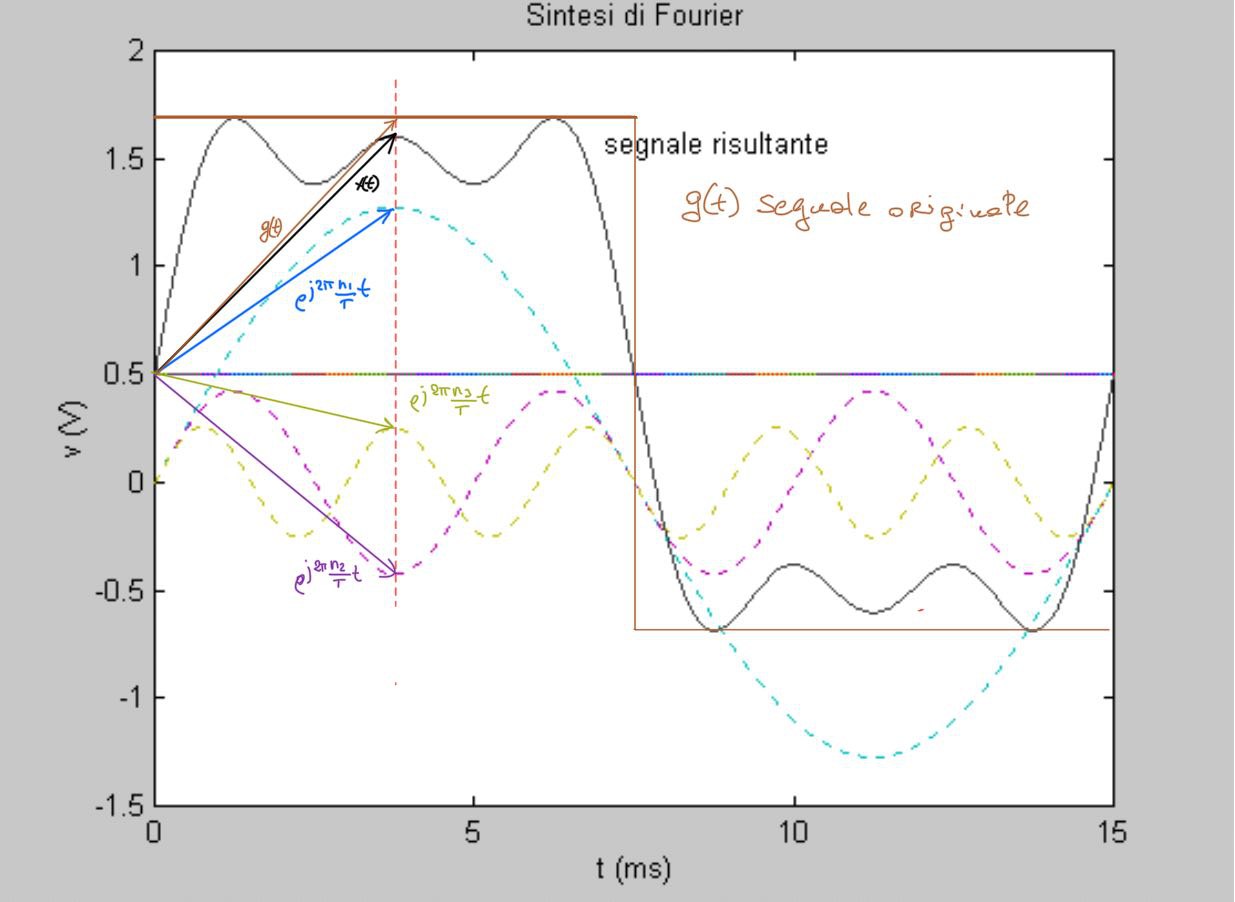
Figure 4: Significato della SDF
- se la base e' completa il vettore \(\vec v\) e' rappresentato esattamente;
se la base non e' completa abbiamo un'approssimazione con un errore \(\vec{x} \perp \vec e\) - vds fig. 5. Per capire l'errore basta guardare la fig 4 in cui il segnale \(x(t)\) e' il risultato di una SDF parziale (\([n_1,n_2,n_3]\)) che differisce dal segnale \(g(t)\) e la differenza tra il \(\vec{e}=\vec{g} - \vec{x}\) che e' perpendicolare alla proiezione di \(\vec{x}\) lungo il versore dell'asse delle ascisse;
Nella pratica comune una qualsiasi funzione periodica \(x(t)\) di periodo T può essere rappresentata nel suo spazio di esistenza da versori complessi del tipo \(\frac{1}{\sqrt T}e^{j2\pi\frac{k}{T}t}\) per cui il coeficente della SDF diventa :
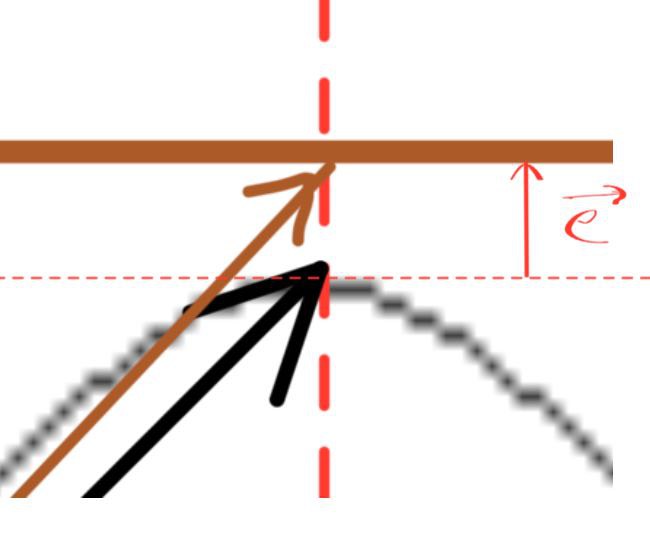
Figure 5: Particolare dalla fig 4 che rappresenta il vettore errore
Per cui la SDF complessa diventa come la seguente in cui ogni termine \(c_k(t)\) e' una sinusoide :
\begin{equation} g(t)=\sum_{k=-\infty}^{\infty}c_k \frac{1}{\sqrt T} e^{j2\pi \frac{k}{T} t} = \sum_{k=-\infty}^{\infty} G_k e^{j2 \pi \frac{k}{T}t}=\sum_{k=-\infty}^{\infty}c_k(t) \end{equation}con
\begin{equation} \label{org43bb59e} G_k = \frac{1}{T} \int_{- T/2}^{T/2} g(t) e^{-j2\pi\frac{k}{T}t} d_{t} \end{equation}2.3. SDF per un segnale non periodico
VDS Trasformata di Fourier
3. Forme della SDF
3.1. SDF in forma reale
Partendo dall'osservazione che
\begin{equation} \label{orge21fed5} g(t)=\sum_{k=-\infty}^{-1} G_ke^{j2\pi\frac{k}{T}t} + G_0 + \sum_{k=1}^{\infty}G_ke^{j2\pi\frac{k}{T}t} \end{equation}invertendo la prima parte della \eqref{orge21fed5} e cambiando di segno all'indice si ottiene4
\begin{equation} g(t)=\sum_{k=1}^{\infty} G_{-k}e^{j2\pi\frac{-k}{T}t} + G_0 + \sum_{k=1}^{\infty}G_ke^{j2\pi\frac{k}{T}t} \end{equation}per cui se \(\phi=e^{j2\pi\frac{k}{T}t}\) allora \(\phi^c=e^{j2\pi\frac{-k}{T}t}\) e \(G_{-k}=G^c_k\), dunque
\begin{equation} \label{eq:006} g(t)=G_0 + \sum_{k=1}^{\infty} [G^c_k\phi^c + G_k\phi] \end{equation}3.2. SDF in forma trigonometrica
Per il passaggio dalla forma reale trigonometrica bisogna ricordare che per le funzioni reali che \(g(t)=X^c(t)\) se anche \(G^c_k\phi^c = G_k\phi\) la \eqref{eq:006} diventa:
\begin{equation} \phi = e^{j2\pi\frac{k}{T}t} =\cos(2\pi\frac{k}{T}t) + j\sin(j2\pi\frac{k}{T}t) \end{equation}ricordando la struttura di un numero complesso \(G_k=A_k+ jB_k\) la \eqref{eq:006} diventa
\begin{equation} \label{eq:0007} \begin{split} G_k\phi_k + G_k^c\phi^c= G_k[\cos(2\pi\frac{k}{T}t)+jsin(2\pi\frac{k}{T}t)] + G_k^c[\cos(-2\pi\frac{k}{T}t) + j sin(-2\pi\frac{k}{T}t)] = \\ = G_k[\cos(2\pi \frac{k}{T} t ) + j sin(2\pi \frac{k}{T} t)] + G_k^c [\cos(2\pi \frac{k}{T} t) - j sin(2\pi \frac{k}{T} t)] = \\ = ... = 2Re\{G_k\} \cos(2\pi \frac{k}{T} t) + 2Im\{G_k\} sin(2\pi \frac{k}{T} t) =\\ = \frac{A_k}{2} \cos(2\pi \frac{k}{T} t) - \frac{B_k}{2} sin(2\pi \frac{k}{T} t) \end{split} \end{equation}Per cui la \eqref{eq:006} la SDF diventa un polinomio trigonometrico del tipo
\begin{equation} g(t)=\frac{A_o}{2} + \sum_{k=1}^{\infty} \frac{A_k}{2}\cos(2\pi\frac{k}{T}t) - \frac{B_k}{2}sin(2\pi\frac{k}{T}t) \end{equation}in cui
\begin{equation} A_k=\frac{2}{T}\int_{-T/2}^{T/2}g(t)\cos(2\pi\frac{k}{T}t) d_t \end{equation} \begin{equation} \label{orgce73076} B_k=\frac{2}{T}\int_{-T/2}^{T/2}g(t)\sin(2\pi\frac{k}{T}t) d_t \end{equation}NB : quando g(t) reale pari \(B_k=0\) quando è reale ed dispari \(A_k=0\).
3.3. SDF in modulo e fase ( polare )
Per esprimere la SDF in modulo e fase basta osservare che
\begin{equation} G_k=\lvert G_k \rvert e^{j\theta} \end{equation}per cui la \eqref{eq:006} può essere riscritta come segue
\begin{equation} \begin{split} g(t)=G_0 + \sum_{k=1}^{\infty}\lvert G_k \rvert e^{j\theta_k}[e^{j2\pi\frac{k}{T}t} + e^{-j2\pi\frac{k}{T}t}]= \\ G_0 + \sum_{k=1}^{\infty}\lvert G_k \rvert 2e^{j\theta_k} 2 \frac{[e^{j2\pi\frac{k}{T}t} + e^{-j2\pi\frac{k}{T}t}]}{2}= \\ G_0 + 2\sum_{k=1}^{\infty}\lvert G_k \rvert \cos(2\pi\frac{k}{T}t + \theta_k) \end{split} \end{equation}in cui \(G_0\) rappresenta il valor medio del segnale.
3.4. Spettro di un segnale
Al fine di meglio comprendere il concetto di spettro di ampiezza e fase si osservi la seguente figura
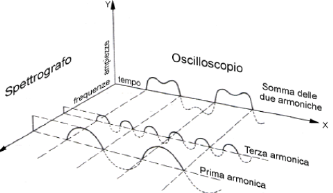
Figure 6: spettro
NB : si definisce fase \(\angle{G_k}=\theta_k\) per cui
| \(g(t)\) | Modulo | Fase | svil. trigonom. |
|---|---|---|---|
| reale | \(G^c_k=G_{-k}\) | \(\angle{G^c_k}=-\angle{G_{-k}}\) | \(\cos\) e \(\sin\) |
| reale pari | \(G_k=G_{-k}\) | \(\angle{G^c_k}=0\) | solo \(\cos\) |
| reale dispari | \(G_k=-G_{-k}\) | \(\angle{G^c_k} \in \{-\frac{\pi}{2}, \frac{\pi}{2}\}\) | solo \(\sin\) |
4. Convergenza della SDF
La convergenza della serie di Fourier è un concetto importante nell'analisi matematica e nella teoria delle serie. La serie di Fourier è utilizzata per rappresentare una funzione periodica come una somma infinita di seni e coseni (o complessi esponenziali). La questione della convergenza è legata a determinare in quali condizioni questa somma infinita approssima correttamente la funzione data.
La serie di Fourier di una funzione
Per quanto riguarda la convergenza, ci sono diverse condizioni che devono essere soddisfatte affinché la serie di Fourier converga alla funzione f(x) su tutto il suo dominio. Alcune di queste condizioni includono:
- La funzione f(x) deve essere periodica con periodo T.
- La funzione f(x) deve essere integrabile su ogni intervallo finito.
- La funzione f(x) deve avere un numero finito di punti di discontinuità di prima specie (discontinuità a salto finito).
Queste condizioni garantiscono la convergenza puntuale della serie di Fourier. Tuttavia, in alcuni casi, potrebbero verificarsi fenomeni come la convergenza in media quadratica o la convergenza puntuale solo in punti di continuità. La teoria della convergenza della serie di Fourier è abbastanza complessa e coinvolge strumenti matematici come la teoria della misura, la teoria dell'integrazione, e il concetto di convergenza in spazi di Hilbert.
In generale, se una funzione soddisfa le condizioni necessarie, la serie di Fourier tende a convergere alla funzione originale quando il numero di termini nella serie aumenta, avvicinandosi sempre di più alla funzione data.
4.1. Condizione di Dirichlet
La condizione di Dirichlet è una delle condizioni che possono essere utilizzate per garantire la convergenza della serie di Fourier per una funzione periodica. Essa è comunemente formulata per una funzione
La condizione di Dirichlet richiede che:
- La funzione f(x) deve essere periodica e di banda limitata, il che significa che deve avere un numero finito di massimi e minimi su ogni periodo T.
- Il numero di punti in cui f(x) ha discontinuità di prima specie (discontinuità a salto finito) deve essere finito su ogni periodo T.
In altre parole, la condizione di Dirichlet impone limiti alla crescita della funzione e al numero di discontinuità per garantire la convergenza della serie di Fourier.
La formulazione matematica della condizione di Dirichlet può essere più precisa, ma l'idea generale è quella di garantire che la funzione sia "abbastanza regolare" e non cresca in modo eccessivo per garantire la convergenza della serie di Fourier.
Se una funzione soddisfa la condizione di Dirichlet, allora la sua serie di Fourier converge puntualmente ai valori di f(x) nei punti di continuità di f(x) e ai punti di discontinuità di f(x) dove f(x) ha limiti destro e sinistro.
La condizione di Dirichlet è una delle condizioni più comuni utilizzate per garantire la convergenza della serie di Fourier, ma ci sono anche altre condizioni, come la condizione di Riemann-Lebesgue, che possono essere utilizzate per studiare la convergenza delle serie di Fourier in contesti specifici.
5. Proprietà della SDF
- comportamento asintotico di \(c_k\) :
- sia n l'ordine di differenziabilità di g(t);
- sia k l'ordine di derivabilità di g(t);
- allora nei punti in cui la SDF di g(t) converge \(c_k \rightarrow 0\) per \(k \rightarrow \infty\) con velocità \(O(\frac{1}{|k|^{n+1}})\);
- L'ordine di differenziabilità coincide con quello di derivabilità quando una funzione è continua mentre se l'ordine differenziabilità è maggiore di quello di derivabilità la funzione è continua a tratti ;
- maggiore è l'ordine di differenziabilità maggiore è la regolarità della funzione e tanto più velocemente \(c_k\) andrà a zero.
- linearità i coeficenti della SDF di un segnale combinazione lineare di altri segnali sono combinazioni lineari dei coeficenti di ogni singola SDF. In conseguenza anche gli spettri sono combinazione lineare di tutti i singoli spettri.
- traslazione temporale i coeficenti della SDF di un segnale traslato nel tempo sono anch'essi traslati nel tempo, cioè : \(x(t-t_0) \Rightarrow c_k(t_0)=c_k\frac{1}{\sqrt(T)}e^{j2\pi \frac{k}{T}t_0}\).
6. Esempio

Figure 7: esempio di calcolo del modulo e fase