Delta di Dirac
Table of Contents
- 1. Scopo
- 2. Funzionale
- 3. Distribuzione
- 4. Delta di Dirac \(\delta(t)\)
- 5. Proprietà
- 6. Limite nel senso delle distribuzioni
- 7. Derivata Distribuzionale
- 8. TDF della delta di DIRAC
- 9. TDF di un segnale periodico
- 10. Pettine di DIRAC
1. Scopo
Permette di estendere il concetto di TDF anche a segnali con discontinuità oppure a segnali periodici rappresentabili con la TDF come ad esempio i segnali ad energia infinita quali, ad esempio, quelli con componente continua.
2. Funzionale
Cambio di paradigma sul significato dell'integrale non più come somma di Reiman ma come funzione che associa ad ogni valore del suo argomento ( funzione ) uno scalare. Un funzionale è definito come segue :
\(I_{\phi(t)}=\int_{a}^b f(t)\phi(t)d_{t}\)
in cui \(\phi(t)\) è una funzione di test a supporto compatto, cioè \(\phi(t) \in C^{\infty}\) è diversa da zero in \([a,b]\) che da significato all'integrale. Ad esempio se \(\phi(t)=1\) allora \(I_{\phi}\) è l'area dell'integrale.
2.1. Proprietà
- linearità : ereditata dall'integrale;
- continuità : \(\phi(t)\) è continua se lo è anche \(f(t)\) cioè \(lim_{\epsilon \rightarrow 0}f(t+\epsilon)=f(t)\), allora:
3. Distribuzione
Quando un funzionale è lineare e continuo allora è una distribuzione.
4. Delta di Dirac \(\delta(t)\)
E' quella funzione t.c. il suo funzionale per qualunque funzione di test risulta \(\phi(0)=\int \delta(t)\phi(t)d_{t}\)
4.1. Giustificazione dell' esistenza
In riferimento alla 1 in cui \(u_{\epsilon}(t)\) è continua su tutto R cioè \(\lim_{\epsilon \rightarrow 0}u_{\epsilon}(t)=u(t)\). Dunque \(u_{\epsilon(t)}\) ammette derivata \(\delta_{\epsilon}(t)\) la quale però non è continua nell'intervallo \(]-\infty,\infty[\).
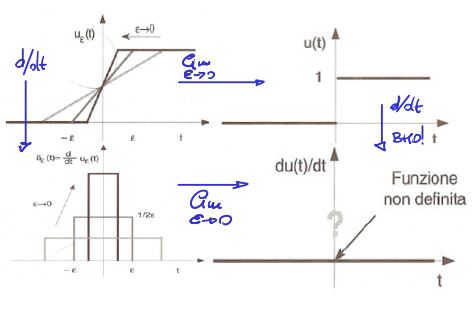
Figure 1: Giustificazione dell'esistenza della \(\delta(t)\)
E' però lecito scrivere
\(\lim_{\epsilon \rightarrow 0}\delta_{\epsilon}(t) = funzione\ di\ base\ nulla\ e\ altezza\ infinita\)
che chiameremo \(\delta(t)\) definita solo in 0. Inoltre è possibile scrivere :
\(u(t)=\lim_{\epsilon \rightarrow 0}u_{\epsilon}(t)=\lim_{\epsilon \rightarrow 0}\int \delta_{\epsilon} d_{t}=\int \lim_{\epsilon \rightarrow 0} \delta_{\epsilon}(t)d_{t}= \int \delta(t) d_{t}\)
che definisce il significato di funzionale permettendo di estendere il significato di derivata: \(\frac{d}{d{t}}u(t)=\delta(t)\).
Inoltre partendo dall'osservazione che :
- l'area sottesa a \(\delta{\epsilon(t)}\) è sempre 1 \(\forall \epsilon\);
- \(\int \delta(t)d_{t}=\int \delta(t) 1 d_{t}=\int \delta(t) \phi(t) d_{t}=\phi(0)\) che altro non è la definizione di delta di D.;
allora essendo \(\phi(t)=1\) il funzionale rappresenta l'area sottesa a \(\delta(t)\) e che corrisponde al salto di \(u(t)\) che altro non e' che il significato analitico.
5. Proprietà
- proprietà campionatrice : La relazione \(\int \delta(t)\phi(t)d_{t}=\phi(0)\) è conosciuta come la proprietà campionatrice della delta di Dirac. Infatti \(\int \delta(t)f(t)d_{t}=\int \delta(0)f(0)d_{t}=f(0)\) in quanto la delta di D. è definita solo in 0.
- Simmetria : \(\delta(t)=\delta(-t)\)
- covoluzione : \(g(t)*\delta(t)=\int g(t)\delta(t-\alpha)d_{t}=g(\alpha)\) in pratica la covoluzione restituisce l'identita';
- Moltiplicazione per uno scalare : \(\int A\delta(t)d_{t}=A\)
6. Limite nel senso delle distribuzioni
7. Derivata Distribuzionale
Per comprendere il significato della derivata distribuzionale ci si basa sulla proprietà della derivazione del prodotto di funzioni:
\(\frac{d}{d_{t}}f(t)\phi(t)=f'(t)\phi{t}+f(t)\phi'(t)\)
da cui :
\begin{equation}\begin{split} \int \frac{d}{d_{t}}f(t)\phi(t) d_{t}= \\ \int f'(t)\phi{t}+f(t)\phi'(t)d_{t}=\\ \int f'(t)\phi{t} d_{t} + \int f(t)\phi'(t) d_{t} \\ \end{split}\end{equation} \begin{equation}\begin{split} \int f'(t)\phi(t)d_{t}= [f(t)\phi(t) ]^{t=\infty}_{t=-\infty} - \int f(t)\phi'(t) d_{t}\\ \end{split}\end{equation} \begin{equation}\begin{split} \int f'(t)\phi(t)d_{t}= - \int f(t)\phi'(t) d_{t}\\ \end{split}\end{equation}in cui \([f(t)\phi(t) ]^{t=\infty}_{t=-\infty}=0\) in quanto \(\phi(t)\) è a supporto compatto, inoltre essendo \(\phi(t)\) una funzione di test che scelgo in modo arbitrario ne conosco la derivata per cui in conseguenza conosco la derivata della distribuzione ( vds 2 ).
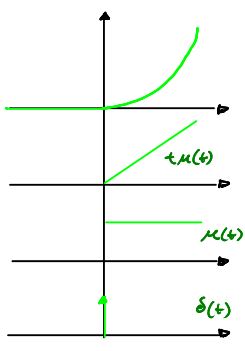
Figure 2: riepilogo della prop. della derivata
7.1. Esempio
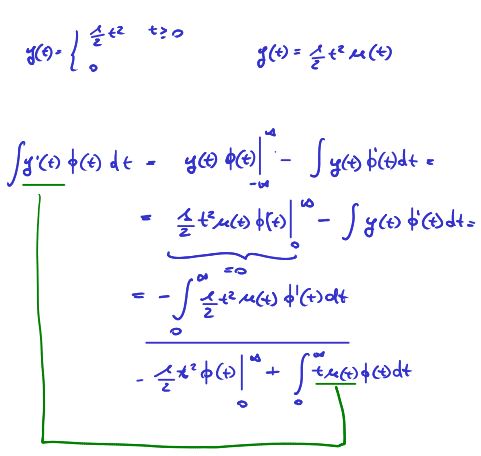
Figure 3: esempio di applicazione di proprietà della derivata
8. TDF della delta di DIRAC
8.1. Definizione
Dalla definizione di TDF si ricava quella per la delta di D. che \(\delta(f)=\int \delta(t) e^{-j2\pi ft}d_{t}=1\) in quanto \(\delta(t)\neq 0\) solo in \(0\).
8.2. Covoluzione
Per la proprietà covolutiva della TDF si ha che \(g(t)*\delta(t) \Rightarrow \int g(t)\delta(t -t_0) \Rightarrow \int G(f)\delta(f - f_{0})=G(f_{0})\) in quanto la delta di D. è non nulla solo in \((f-f_{0})\) proprietà di campionamento della delta di D. .
8.3. TDF di un segnale complesso
Senza l'introduzione della delta di D. questa TDF non avrebbe senso in quanto l'energia di g(t) è infinita. Con l'uso della proprieta' della modulazione otteniamo :
\(g(t)=e^{j2\pi f_{0}t}=1 e^{j2\pi f_{0}t} \Rightarrow G(f)=\delta(f-f_{0})\)
8.3.1. esempio :
TDF di \(g(t)=cos(2\pi f_{0} t)= \frac{e^{j2\pi f_{0}t} + e^{-j2\pi f_{0}t}}{2}\)
\(g(t) \Rightarrow G(f)=\frac{1}{2}(\delta(f - f_{0}) + \delta(f + f_{0}))\)
8.4. TDF di u(t)
8.4.1. TDF della funzione \(g(t)=e^{-bt}\) per \(t >=0\)
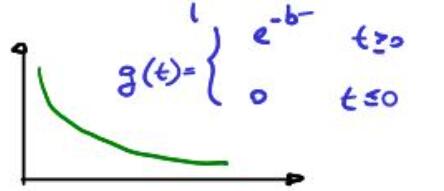
Figure 4: funzione \(e^{-bt}\) e sua TDF
Per trovare la trasformata di Fourier della funzione \(e^{-bt}u(t)\) segui questi passaggi:
Definizione della Funzione:
Sia \(e^{-bt}\) una funzione esponenziale decrescente con \(b\) positivo
Quindi, la funzione \(e^{-bt}u(t)\) è:
- \(0\) per \(t < 0\),
- \(e^{-bt}\) per \(t \geq 0\).
Trasformata di Fourier:
La trasformata di Fourier di una funzione \(f(t)\) è data da:
\begin{equation} \mathcal{F}\{f(t)\} = \int_{-\infty}^{\infty} f(t) e^{-j2\pi f t} dt \end{equation}Per la funzione \( e^{-bt}u(t) \), l'integrale diventa:
\[ \mathcal{F}\{e^{-bt}u(t)\} = \int_{-\infty}^{\infty} e^{-bt}u(t) e^{-j2\pi f t} \, dt \]
Poiché \( u(t) = 0 \) per \( t < 0 \), l'integrale si riduce a:
\[ \mathcal{F}\{e^{-bt}u(t)\} = \int_{0}^{\infty} e^{-bt} e^{-j2\pi f t} \, dt \]
Combinando le esponenziali, otteniamo:
\[ \mathcal{F}\{e^{-bt}u(t)\} = \int_{0}^{\infty} e^{-(b + j2\pi f)t} \, dt \]
Calcoliamo l'Integrale:
L'integrale da risolvere è:
\[ \int_{0}^{\infty} e^{-(b + j2\pi f)t} \, dt \]
L'antiderivata di \( e^{-(b + j2\pi f)t} \) è:
\[ \int e^{-(b + j2\pi f)t} \, dt = \frac{e^{-(b + j2\pi f)t}}{-(b + j2\pi f)} + C \]
Applicando i limiti di integrazione da 0 a \( \infty \):
\[ \mathcal{F}\{e^{-bt}u(t)\} = \left[ \frac{e^{-(b + j2\pi f)t}}{-(b + j2\pi f)} \right]_{0}^{\infty} \]
Calcoliamo i limiti:
- Per \( t \to \infty \), \( e^{-(b + j2\pi f)t} \to 0 \) (dato che \( b > 0 \)).
- Per \( t = 0 \), \( e^{-(b + j2\pi f) \cdot 0} = 1 \).
Quindi:
\[ \mathcal{F}\{e^{-bt}u(t)\} = \frac{0 - 1}{-(b + j2\pi f)} = \frac{1}{b + j2\pi f} \]
Quindi, la trasformata di Fourier della funzione \( e^{-bt}u(t) \) è:
\[ \mathcal{F}\{e^{-bt}u(t)\} = \frac{1}{b + j2\pi f} \]
dove \( b > 0 \).
8.4.2. TDF della funzione sgn(t) intesa come limite per \(b \rightarrow 0\) della funzione \(e^{-bt}\) estesa all'infinito
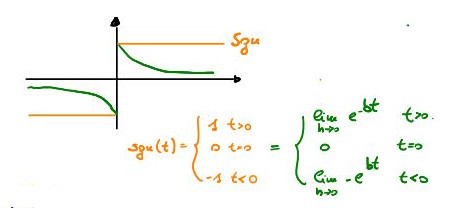
Figure 5: funzione \(sgn(t)\) e sua TDF
Per trovare la trasformata di Fourier della funzione di cui all fig. 5 segui questi passaggi:
Definizione della Funzione:
Sia \(f(t)\) una funzione esponenziale con t.c.
- \(f(t)=e^{-bt}\) con \(b>0\) per \(t>0\),
- \(0\) per \(t =0\),
- \(e^{bt}\) con \(b>0\) per \(t < 0\).
- Scrittura della trasformata di Fourier: La trasformata di Fourier \( \hat{f}(2\pi f) \) di una funzione \( f(t) \) è data da:
combinando la \eqref{eq:000} e la \eqref{eq:001} ottengo la \eqref{eq:002}
\begin{equation} \label{eq:002} \begin{split} -\frac{1}{-j2\pi f} + \frac{1}{j2\pi f} = \frac{2}{j2\pi f}=\frac{1}{j\pi f} \end{split} \end{equation}8.4.3. TDF di u(t) intesa come traslazione verticale della funzione \(sgn(t)\)
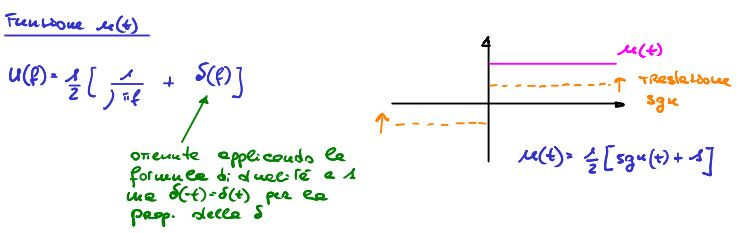
Figure 6: funzione \(u(t)\) e sua TDF
9. TDF di un segnale periodico
Sia \(X_{T}(t)=rect(\frac{t-n T_0}{T_0})x(t)\) la troncata centrata in \(T_0\) relativa al periodo base di un segnale periodico \(x(t)\) e sia
\begin{equation} \begin{split} X_{p}(t)=\sum_{n=-\infty}^{n=\infty} X_{T}(t - nT_{0})=\\ \sum_{n=-\infty}^{n=\infty} G(n)e^{j2\pi \frac{n}{T_{0}}t } \end{split} \end{equation}la ridefinizione del segnale periodico in cui l'ultima uguaglianza si ricava dalla definizione della SDF dove il coeficente si ottiene dalla seguente :
\begin{equation} \label{eq:4} \begin{split} G(n)=\frac{1}{T_0}\int_{-\infty}^{\infty}X_{T}(t)e^{-j2\pi \frac{n}{T_{0}}t}d_{t} = \\ \frac{1}{T_{0}} \int_{-\infty}^{\infty} x(t)rect(\frac{t -n T_0}{T_0})e^{-j2\pi \frac{n}{T_{0}}t}d_{t}=\\ \frac{1}{T_{0}} \int_{-T_{0}/2}^{T_{0}/2} x(t)e^{-j2\pi \frac{n}{T_{0}}t}d_{t} = \\ f_{0}\int_{-T_{0}/2}^{T_{0}/2} x(t)e^{-j2\pi nf_{0}t}d_{t}=f_{0}G(nf_{0}) \end{split} \end{equation}in cui l'ultima uguaglianza è ottenuta con la sostituzione \(f_{0}=\frac{1}{T_{0}}\) per cui la SDF può essere riscritta come :
\(X_{p}(t)=f_{0}\sum_{n=-\infty}^{n=\infty}G(f)e^{j2\pi nf_{0}t }\)
ed applicando la TDF di un segnale complesso si ottiene
\(X_{p}(t) \Rightarrow X_p(f)=f_{0}\sum_{n=-\infty}^{n=\infty}G(f)\delta(f - nf_{0})\)
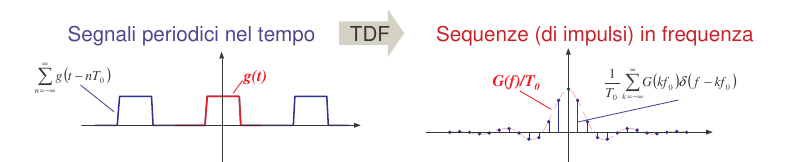
Figure 7: TDF di un segnale periodico
10. Pettine di DIRAC
Sia
\begin{equation} \label{eq:101 } \begin{split} x_p(t)=\sum_{n=-\infty}^{n=\infty}\delta(t - nT_{0}) \end{split} \end{equation}un segnale periodico come mostrato in fig. 8 che in analogia con quanto visto per i segnali periodici \(x_p(t)\) può essere riscritto come ripetizione della troncata ottenuta come prodotto delta centrata in \(0\)
\begin{equation} \label{eq:102 } \begin{split} \delta(t -nT_0)=rect(\frac{t-nT_0}{T_0})\delta(t) \end{split} \end{equation}per cui
\begin{equation} \label{org955ca1a} \begin{split} x_p(t)=\sum_{n=-\infty}^{n=\infty}\delta(t -nT_0)=\\ \sum_{n=-\infty}^{n=\infty}rect \left( \frac{t - nT_0}{T_0} \right ) \delta(t)=\\ \sum_{n=-\infty}^{n=\infty}G_{\delta}(n)e^{j2\pi \frac{n}{T_{0}}t} \end{split} \end{equation}dove il coeficente della SDF ( in analogia con la \eqref{eq:4} ) vale :
\begin{equation}\begin{split} \label{orga483ad3} G_{\delta}(n)=\frac{1}{T_{0}}\int_{-\infty}^{\infty}rect \left ( \frac{t - nT_0}{T_0} \right ) \delta(t)e^{-j2\pi \frac{n}{T_{0}}t}d_{t}=\\ \frac{1}{T_{0}}\int_{-T_{0}/2}^{T_{0}/2} \delta(t) e^{-j2\pi \frac{n}{T_{0}}t}d_{t}=\\ \frac{1}{T_{0}} \int_{-T_{0}/2}^{T_{0}/2} 1 d_{t}=f_0 \end{split}\end{equation}e dunque la SDF diventa
\begin{equation} \label{org1ba5c51} x_p(t)=f_{0}\sum_{n=-\infty}^{n=\infty} 1e^{j2\pi nf_{0}t} \end{equation}la cui TDF, per la definizione di TDF di funzione periodica diventa :
\begin{equation} \label{org96ef55d} x_{p}(t) \Rightarrow X_{p}(f)=f_{0}\sum_{n=-\infty}^{n=\infty} \delta(f - nf_{0}) \end{equation}L'immagine nel seguito mostra la rappresentazione del pettine di Dirac
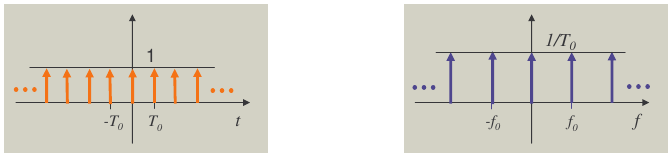
Figure 8: Pettine di Dirac